Обзор программных операторов.

Вплоть до появления 7 версии системы MathCAD возможности программирования в них были крайне ограниченными. Фактически MathCAD позволяла реализовать лишь линейные программы, в основе которых лежит понятие функции. Функция if и ранжированные переменные в отдельных случаях могли заменить условные выражения и циклы, но с серьезными ограничениями. Отсутствовала возможность задания завершенных программных модулей.

Эти возможности в расширенном варианте появились в MathCAD 7.0 Pro и имеются в описываемой версии MathCAD 2001 PRO. Они сосредоточены в наборной панели программных элементов Programming (показана на рисунке), включаемой кнопкой на панели Math.

Отметим, что возможность составлять программы реализована только в версии Professional. Все эти MathCAD-программы с точки зрения программиста представляют собой подпрограммы-функции, которые могут возвращать в качестве результата число, вектор или матрицу. Функции могут вызывать сами себя (рекурсивно определенные функции) или другие подпрограммы-функции, определенные выше в том же MathCAD-документе.

Эти подпрограммы-функции составляются так же, как и определения функций. Рассмотрим простой пример вычисления суммы: Sum(n)=1+2+3+..+n:

• Задайте сначала имя функции Sum, вслед за которым введите список параметров (n) и оператор присваивания :=
• Введите начальное значение s <-- 0 и отметьте его целиком. Стрелка служит оператором присваивания в теле программы, вводитя клавишей { (открывающая фигурная скобка) или выбором кнопки со срелкой с панели.
• Создайте новую строку программы (вставка вертикальной черты) при помощи кнопки Add Line ( клавиша -] (закрывающая квадратная скобка)). На экране появится вертикальная черта и пустая ячейка.
• Выполните щелчок на кнопке for, чтобы ввести оператор цикла. Перед символом принадлежности введите переменную i, а после него - промежуток изменения переменной 1..n. В находящейся ниже ячейке введите присваивание s <- s+i. Программа готова.

Ниже в таблице приведены операторы, находящиеся на кнопках панели программирования.

Команды панели Symbolic (символы)
Команда	Функция	Пример
Add Line	Добавляет новую строку под/над (зависит от выделения) текущей строкой.
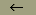	Присваивание значения локальной переменной.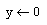
if	Условный оператор (оператор ветвления)if; условие должно стоять после if, а оператор, который исполняется, если выполнено заданное условие,- перед if.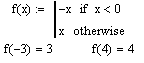
otherwise	Обозначает оператор, который должет быть исполнен, если условие оператора if не выполняется.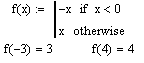
for	Цикл for; за ключевым словом for следует переменная-счетчик, а после символа принадлежности вводится промедуток изменения этой переменной. Внутренние операторы цикла сдвинуты немного вправо.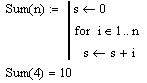
while	Цикл while;внутренние операторы цикла будут исполняться до тех пор, пока будет истинным условие, следующее за ключевым словом while. Пример показыветприменение цикла для нахождения нулей функции методом касательных Ньютона.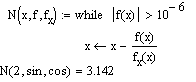
break	Служит для преждевременного завершения цикла, чтобы, например, избежать зацикливания или слишком продолжительных вычислений.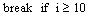
continue	Служит для преждевременного завершения текущей итерации цикла; сам цикл при этом продолжается.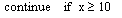
retutn	Преждевременное завершение программы; указанное в ячейке значение будет возвращено.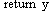
on error	Если при вычислении выражения expr2 возникла ошибка, вычисляется выражение expr1.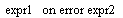

Примеры программ.

Условный оператор if и оператор otherwise.Рассмотрим пример программного блока, вычисляющего факториал с использованием рекурсии

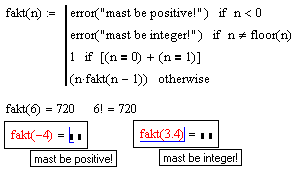В данном примере 1 возвращается, только если n=0 или n=1. Обратите внимание на задание некольких условий - со знаком плюс, каждое условие в скобках. В остальных случаях, учитывая формулу n!=n*(n-1)!, вызывается fakt(n-1) и умножается на n. При помощи функции error можно вывести сообщение об ошибке при неправильном вводе аргумента.

Для демонстрации работы цикла for рассмотрим ту же задачу, но вычисление факториала осуществим при помощи цикла.

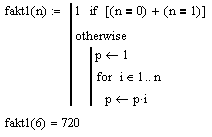Если n=0 или n=1, возвращается 1, в противном случае при помощи цикла for вычисляется произведение n!=1*2*3...*n. Вычисленное последним значениеpвозвращается автоматически.

В следующем примере при помощи алгоритма Евклида определяется наибольший общий делитель. Для реализации алгоритма используется цикл с ключевым словом while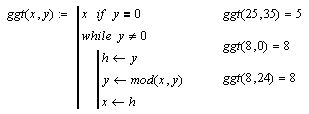

Прерывание цикла при помощи операторов break и continue. Оператор return.Первый пример - релизация метода касательных Ньютона для определения нулей функции. На основе начального значения x вычисляется новое улучшенное значение x, расположенное ближе к искомому нулю функции. При этом итерации повторяются до тех пор, пока значение функции не станет меньше заданной точности (в примере 10^-6).

При помощи оператора return организовано завершение программы в нужный момент. В данном примере если число итераций больше или равно 10, то происходит прерывание программы и выдается сообщение о том, что слишком много итераций. Здесь также отслеживаются случаи, когда производная в знаменателе близка к нулю и выдается об этом сообщение.

Кроме ключевого слова break имеется ключевое слово continue с похожей функцией. В то время как break прерывает цикл и осуществляет переход к следующему за циклом оператору, continue прерывает выполнение только текущей итерации. В примере справа ключевое слово continue используется для выявления всех нулей функции на заданном интервале. При этом в примере производится разбиение интервала на n равных подинтервалов и ищутся те из них, на которых функия меняет знак. При обнаружении такого поинтервала вызывается функия, реализующая метод касательных Ньютона, с начальным значением, находящимся в середине подинтервала.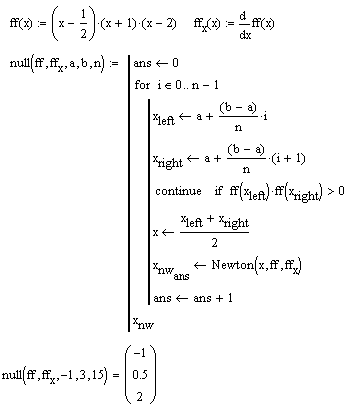

Обратите внимание, по завершении работы программы выдается вектор значений.

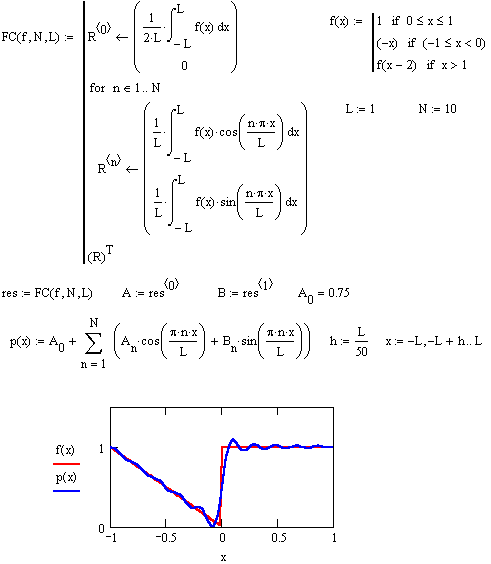
Ниже приводится программа, вычисляющая коэффициенты Фурье функции, причем в результате выдается матица значений: нулевая по счету строка содержит коэффициенты А_n, а первая - коэффициенты B_n. Для выделения этих коэффициентов выдавемая матрица транспонируется и из нее выбирается нулевой столбец для коэффициентов А_n, и первый - для B_n.

Лекция 7.
Интерполяция и регрессия, функции сглаживания данных и предсказания.

7.1 Функции линейной и сплайновой аппроксимации.
7.2 Функции для проведения регрессии.
7.3 Функции сглаживания данных.
7.4 Функция предсказания.
7.5 Задания.