Движение в сторону градиента функции.
Промежуточные точки на поверхности отклика рассчитываются по следующей схеме:
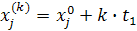 .
.
Для облегчения вычислений рекомендуется использовать Microsoft Office Excel.
Заполняется следующая таблица:
| Δx1 | Δx2 | Δx3 | 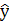 (считается по формуле (1)) (считается по формуле (1)) | |
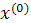 | 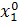 | 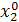 | 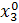 | |
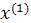 | 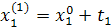 | 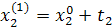 | 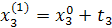 | |
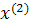 | 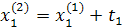 | 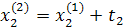 | 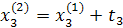 | |
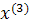 | 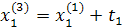 | 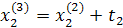 | 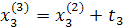 | |
| … | … | … | … |
5. Находим экстремальное значение (минимум или максимум). Движение прекращаем, если:
1) найдено экстремальное значение. Определяем максимум это или минимум;
2) определили, что функция монотонна (наибольшее или наименьшее значение функция принимает в начальной точке, а при движении по поверхности отклика постоянно возрастает или же убывает).
Контрольные вопросы.
1. Какие эксперименты называют оптимизационными?
2. Какие методы используют для оптимизации и нахождения экстремума?
3. Принцип метода Гаусса-Зейделя.
4. Метод конфигураций.
5. Симплексные алгоритмы. Разновидности. Отличия.
6. Градиентные методы.
7. Опишите метод крутого восхождения Бокса-Уилсона.
8. Какая задача стояла при выполнении лабораторной работы № 4? Какие выводы можно сделать после выполнения поставленной задачи?
Библиография
1. Ахназарова С. Л., Кафаров В. В. Оптимизация эксперимента в химии и химической технологии: учеб. Пособие для химико-технологических вузов.- М.: Высш. Школа, 1978. – 319 с.
2. Казаков Ю. Б. Методы планирования эксперимента – М.: Энергия, 1971, 7 с.
3. Кринецкий И.И. Основы научных исследований: учеб. пособие для вузов – Киев – Одесса, Вища школа. – Головное изд-во, 1981 – 208 с.
4. Шмитько, Е.И. Процессы и аппараты в технологии строительных материалов и изделий: учебное пособие/ Е.И. Шмитько, Воронеж. гос. арх.- строит. у-т.- Воронеж, 2007.- Т.1 (вопросы теории).-261 с.
5. Методы безусловной многомерной оптимизации: Рек. к выполнению лаб., практ. и курсовых работ/ Сост.: С.А. Шипилов: НФИ КемГУ. – Новокузнецк. 2000.- 31 с.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1
Значение критерия Фишера F1-p для надежности оценки p=0,05
| Число степеней свободы, f2 | Число степеней свободы, f1 | |||||||
| 164,4 | 199,5 | 215,7 | 224,6 | 230,2 | 234,0 | 244,9 | ||
| 18,5 | 19,2 | 19,2 | 19,3 | 19,3 | 19,3 | 19,4 | 19,5 | |
| 10,1 | 9,6 | 9,3 | 9,1 | 9,0 | 8,9 | 8,7 | 8,6 | |
| 7,7 | 6,9 | 6,6 | 6,4 | 6,3 | 6,2 | 5,9 | 5,8 | |
| 6,6 | 5,8 | 5,4 | 5,2 | 5,1 | 5,0 | 4,7 | 4,5 | |
| 6,0 | 5,1 | 4,8 | 4,5 | 4,4 | 4,3 | 4,0 | 3,8 | |
| 5,6 | 4,7 | 4,4 | 4,1 | 4,0 | 3,9 | 3,6 | 3,4 | |
| 5,3 | 4,5 | 4,1 | 3,8 | 3,7 | 3,6 | 3,3 | 3,1 | |
| 5,1 | 4,3 | 3,9 | 3,6 | 3,5 | 3,4 | 3,1 | 2,9 | |
| 5,0 | 4,1 | 3,7 | 3,5 | 3,3 | 3,2 | 2,9 | 2,7 | |
| 4,8 | 4,0 | 3,6 | 3,4 | 3,2 | 3,1 | 2,8 | 2,6 | |
| 4,8 | 3,9 | 3,5 | 3,3 | 3,1 | 3,0 | 2,7 | 2,5 | |
| 4,7 | 3,8 | 3,4 | 3,2 | 3,0 | 2,9 | 2,6 | 2,4 | |
| 4,6 | 3,7 | 3,3 | 3,1 | 3,0 | 2,9 | 2,5 | 2,3 | |
| 4,5 | 3,7 | 3,3 | 3,1 | 2,9 | 2,8 | 2,5 | 2,3 | |
| 4,5 | 3,6 | 3,2 | 3,0 | 2,9 | 2,7 | 2,4 | 2,2 | |
| 4,5 | 3,6 | 3,2 | 3,0 | 2,8 | 2,7 | 2,4 | 2,2 | |
| 4,4 | 3,6 | 3,2 | 2,9 | 2,8 | 2,7 | 2,3 | 2,1 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,3 | 2,1 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,3 | 2,1 | |
| 4,3 | 3,4 | 3,1 | 2,8 | 2,7 | 2,6 | 2,2 | 2,0 | |
| 4,3 | 3,4 | 3,0 | 2,8 | 2,6 | 2,5 | 2,2 | 2,0 | |
| 4,2 | 3,4 | 3,0 | 2,7 | 2,6 | 2,5 | 2,2 | 2,0 | |
| 4,2 | 3,3 | 3,0 | 2,7 | 2,6 | 2,4 | 2,1 | 1,9 | |
| 4,2 | 3,3 | 2,9 | 2,7 | 2,5 | 2,4 | 2,1 | 1,9 | |
| 4,1 | 3,2 | 2,9 | 2,6 | 2,5 | 2,3 | 2,0 | 1,8 | |
| 4,0 | 3,2 | 2,8 | 2,5 | 2,4 | 2,3 | 1,9 | 1,7 | |
| 3,9 | 3,1 | 2,7 | 2,5 | 2,3 | 2,2 | 1,8 | 1,6 |
ПРИЛОЖЕНИЕ 2
Значения критерия Стьюдента t
| число степеней свободы f | Уровни значимости p | ||||
| 0,10 | 0,05 | 0,02 | 0,01 | 0,001 | |
| 6,31 | 12,71 | 31,82 | 63,66 | 636,62 | |
| 2,92 | 4,30 | 6,97 | 9,93 | 31,60 | |
| 2,35 | 3,18 | 4,54 | 5,84 | 12,94 | |
| 2,13 | 2,78 | 3,75 | 4,60 | 8,61 | |
| 2,02 | 2,57 | 3,37 | 4,03 | 6,86 | |
| 1,94 | 2,45 | 3,14 | 3,11 | 5,96 | |
| 1,90 | 2,37 | 3,00 | 3,50 | 5,41 | |
| 1,86 | 2,31 | 2,90 | 3,36 | 5,04 | |
| 1,83 | 2,26 | 2,82 | 3,25 | 4,78 | |
| 1,81 | 2,23 | 2,76 | 3,11 | 4,59 | |
| 1,80 | 2,20 | 2,72 | 3,11 | 4,44 | |
| 1,78 | 2,18 | 2,68 | 3,06 | 4,32 | |
| 1,77 | 2,16 | 2,65 | 3,01 | 4,22 | |
| 1,76 | 2,15 | 2,62 | 2,98 | 4,14 | |
| 1,75 | 2,13 | 2,60 | 2,95 | 4,07 | |
| 1,75 | 2,12 | 2,58 | 2,92 | 4,02 | |
| 1,74 | 2,11 | 2,57 | 2,90 | 3,97 | |
| 1,73 | 2,10 | 2,55 | 2,88 | 3,92 | |
| 1,73 | 2,09 | 2,54 | 2,86 | 3,88 | |
| 1,73 | 2,09 | 2,53 | 2,85 | 3,85 | |
| 1,72 | 2,08 | 2,52 | 2,83 | 3,82 | |
| 1,72 | 2,07 | 2,51 | 2,82 | 3,79 | |
| 1,71 | 2,07 | 2,50 | 2,81 | 3,77 | |
| 1,71 | 2,06 | 2,49 | 2,80 | 3,75 | |
| 1,71 | 2,06 | 2,48 | 2,79 | 3,73 | |
| 1,71 | 2,06 | 2,48 | 2,78 | 3,71 | |
| 1,70 | 2,05 | 2,47 | 2,77 | 3,69 | |
| 1,70 | 2,05 | 2,47 | 2,76 | 3,67 | |
| 1,70 | 2,04 | 2,46 | 2,76 | 3,6 | |
| 1,70 | 2,04 | 2,46 | 2,75 | 3,65 | |
| 1,68 | 2,02 | 2,42 | 2,70 | 3,55 | |
| 1,67 | 2,00 | 2,39 | 2,66 | 3,46 | |
| 1,66 | 1,98 | 2,36 | 2,62 | 3,37 | |
 ∞ ∞ | 1,64 | 1,96 | 2,33 | 2,58 | 3,29 |
ПРИЛОЖЕНИЕ 3
Варианты заданий
Для планирования 3-факторного эксперимента:
Вариант 1
Определить влияние следующих факторов:
1. расхода (1300 – 1900 т/ч);
2. общей щелочности (0,05 – 1,05 мг-экв/л);
3. температуры исходной воды(10 – 32˚ С)
на остаточное содержание свободного диоксида углерода (мг/дм) в декарбонизованной воде.
Вариант 2
Определить влияние следующих факторов:
1. нагрузки деаэратора (400 – 800 т/ч);
2. общей щелочности (0,4 – 0,85 мг-экв/л);
3. температуры исходной воды (32 – 66˚ С)
на рН деаэрированной воды.
Вариант 3
Определить влияние следующих факторов:
1. давления на входе в напорный канал установки обратного осмоса (0,5 – 1,1 МПа);
2. расстояния между прижимными плитами (137 – 140мм);
3. температуры исходной воды (10 – 32˚ С)
на:
а) производительность установки обратного осмоса (дм/ч);
б) концентрацию хлорида натрия в фильтрате (г/дм).
Вариант 4
Определить влияние на концентрацию коагулянта, подаваемого в «Осветлитель», следующих показателей:
а)
1. прозрачности исходной воды (190 – 311 мм);
2. концентрации железа (400 – 838 мкг/кг);
3. нагрузки «Осветлителя» ( 134 – 316 т/ч);
б)
1. окисляемости исходной воды (6 – 10 мг/дм);
2. концентрации железа (150 – 750 мкг/кг);
3. концентрации извести (550 – 750 мг-экв/дм).
Для планирования 2-факторного эксперимента:
Вариант 5
Определить влияние на концентрацию коагулянта, подаваемого в «Осветлитель», следующих показателей:
а)
1. прозрачности исходной воды (100 – 300 мм);
2. нагрузки «Осветлителя» (100 – 300 т/ч);
б)
1. концентрации железа (220 – 800 мкг/кг);
2. нагрузки «Осветлителя» (100 – 300 т/ч).
Экспериментальные данные для вариантов представлены
в таблицах 1, 2.
Таблица 1
| Номер опыта | Значения исследуемых факторов | Варианты | |||||||
| условные единицы | |||||||||
| х1 | х2 | х3 | а | б | а | б | |||
| -1 +1 -1 +1 -1 +1 -1 +1 -1,21 +1,21 | -1 -1 +1 +1 -1 -1 +1 +1 -1,21 +1,21 | -1 -1 -1 -1 +1 +1 +1 +1 -1,21 +1,21 | 1,86 2,56 2,47 3,03 3,5 3,17 3,26 4,38 2,8 3,4 2,6 3,5 2,7 4,23 3,43 | 9,9 8,1 10,099 9,73 8,3 6,89 9,35 8,3 10,2 8,7 7,3 9,5 10,3 | 0,6 1,25 1,16 1,8 0,66 1,31 1.91 1,85 0,85 1,62 0,87 1,6 1,12 1,26 1,23 |
Таблица 2
| Номер опыта | Значения исследуемых факторов | Вариант 5 | ||||
| условные единицы | ||||||
| х1 | х2 | а | б | |||
| -1 +1 -1 +1 +1 -1 | -1 -1 +1 +1 +1 -1 | |||||
Результаты параллельных опытов для вариантов представлены в таблицах 3, 4
Таблица 3
| Номер опыта | Варианты | |||||||||||||||||
| 3а | 3б | 4а | 4б | |||||||||||||||
| Параллельные опыты | ||||||||||||||||||
| 1,86 2,56 2,47 3,03 3,5 3,17 3,26 4,38 2,8 3,4 2,6 3,5 2,7 4,23 3,43 | 1,86 2,58 2,47 3,03 3,5 3,17 3,26 4,36 2,83 3,43 2,8 3,53 2,7 4,23 3,43 | 9,9 8,1 10,09 9,73 8,3 6,89 9,35 8,3 10,2 8,7 7,3 9,5 10,3 | 9,9 8,2 10,09 9,73 8,3 6,89 9,35 8,3 8,9 7,3 9,5 10,3 | 70,568 67,5 66,5 | 0,6 1,25 1,16 1,8 0,66 1,31 1.91 1,85 0,85 1,62 0,87 1,6 1,12 1,26 1,23 | 0,6 1,25 1,16 1,67 0,66 1,31 1.91 1,85 0,81 1,62 0,87 1,6 1,12 1,26 1,23 | ||||||||||||
Таблица 4
| Номер опыта | Вариант 5 | ||||||||||
| а | б | ||||||||||
Учебное издание
Светлана Владимировна Лапшина
Кристина Юрьевна Романова
ОСНОВЫ НАУНЫХ ИССЛЕДОВАНИЙ
Лабораторный практикум
Редактор Е. М. Марносова
План электронных изданий 2012 г. Поз. № 26В
Подписано в печать. 04.04.2012. Уч-изд. л. 4,68
На магнитоносителе.
Волгоградский государственный технический университет.
400005, г. Волгоград, пр. Ленина, 28, корп. 1.
 |
