Движение в сторону противоположную градиенту функции.
Промежуточные точки на поверхности отклика рассчитываются по следующей схеме:
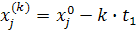 .
.
Например,
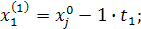
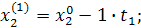
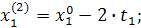
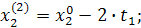
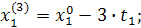
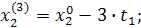
и т.д. и т.д.
Для облегчения вычислений рекомендуется использовать Microsoft Office Excel.
Заполняется следующая таблица:
| Δx1 | Δx2 | 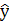 (считается по формуле (1)) (считается по формуле (1)) | |
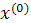 | 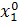 | 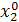 | |
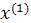 | 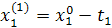 | 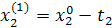 | |
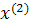 | 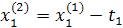 | 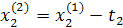 | |
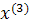 | 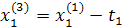 | 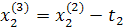 | |
| … | … | … |
Движение в сторону градиента функции.
Промежуточные точки на поверхности отклика рассчитываются по следующей схеме:
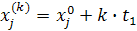 .
.
Заполняется следующая таблица:
| Δx1 | Δx2 | 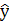 (считается по формуле (1)) (считается по формуле (1)) | |
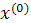 | 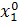 | 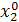 | |
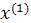 | 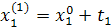 | 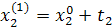 | |
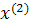 | 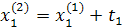 | 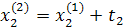 | |
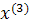 | 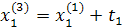 | 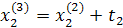 | |
| … | … | … | |
5. Находим экстремальное значение (минимум или максимум). Движение прекращаем, если:
1. найдено экстремальное значение. Определяем максимум это или минимум.
2. Определили, что функция монотонна (наибольшее или наименьшее значение функция принимает в начальной точке, а при движении по поверхности отклика постоянно возрастает или же убывает).
Трехфакторный эксперимент.
1. Выписываем посчитанные при выполнении лабораторной работы № 2 значения шагов варьирования переменных h1, h2, h3 и значения основных уровней 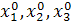 соответственно варианту.
соответственно варианту.
2. В уравнении регрессии, найденном также в лабораторной работе № 2 переходим от кодированных координат к натуральным. Переход осуществляется по формуле:
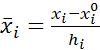 ;
;
где 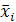 - значение переменной в кодированных координатах,
- значение переменной в кодированных координатах, 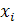 - значение переменной в натуральных координатах.
- значение переменной в натуральных координатах.
Подставим данное выражение в уравнение регрессии:
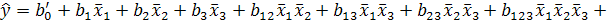
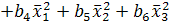 ;
;
подставляем
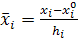 ;
;
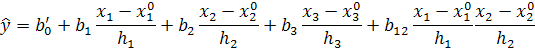
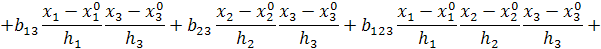
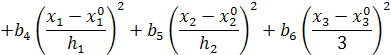
выполним необходимые преобразования и получим уравнение регрессии в натуральном масштабе:
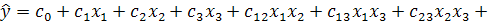
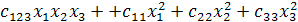 (4.3)
(4.3)
со следующими коэффициентами:
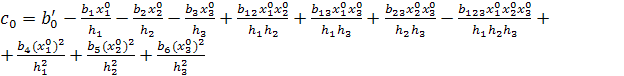
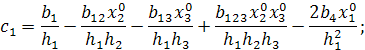
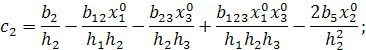
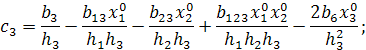
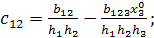
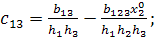
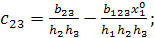
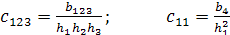 ;
; 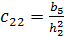 ;
; 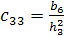 .
.
При проведении расчетов заполняем таблицу:
| Номер опыта | 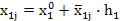 | 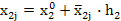 | 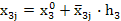 | 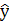 (считается по формуле (2)) (считается по формуле (2)) |
| … | ||||
| … | ||||
3. Вычислим величину шага для имеющихся переменных (факторов) - 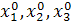 :
:
x1: 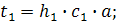
x2: 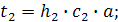
x3: 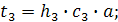
где a – коэффициент пропорциональности, который может принимать любые значения (обычно берут значение, равное 0,1).
4. Начинаем движение по поверхности отклика из начальной точки 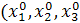 ) при трехфакторной модели.
) при трехфакторной модели.
Движение по поверхности осуществляется в сторону противоположную градиенту функции до тех пор, пока значение функции не начнет увеличиваться, в случае поиска минимума. В случае поиска максимума движение происходит в сторону градиента функции до того момента, пока значения функции не начнут уменьшаться.
Наша задача – пройти поверхность отклика в обе стороны с целью определения экстремума функции.
Движение в сторону противоположную градиенту функции.
Промежуточные точки на поверхности отклика рассчитываются по следующей схеме:
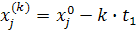 .
.
При трехфакторной модели:
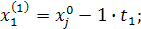
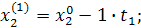
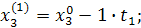
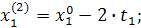
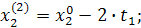
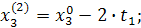
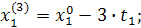
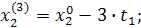
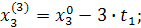
и т.д. и т.д. и т.д.
Для облегчения вычислений рекомендуется использовать Microsoft Office Excel.
Заполняется следующая таблица:
| Δx1 | Δx2 | Δx3 | 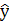 (считается по формуле (2)) (считается по формуле (2)) | |
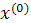 | 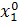 | 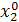 | 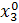 | |
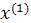 | 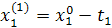 | 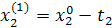 | 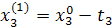 | |
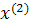 | 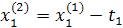 | 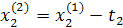 | 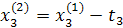 | |
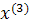 | 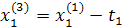 | 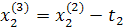 | 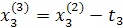 | |
| … | … | … | … |
