Определим значимость коэффициентов регрессии по критерию Стьюдента.

Определяем среднее значение: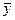

где m – число параллельных опытов, - экспериментальное значение отклика, полученное при параллельных опытах. Данные параллельных экспериментов берем из приложения 3.

Так как есть данные о параллельных опытах, то дисперсию воспроизводимости можно вычислить по следующей формуле :

Коэффициенты уравнения регрессии, получаемые при помощи ортогональных планов второго порядка, определяются с разной точностью, поэтому сначала определяем дисперсии коэффициентов по формуле:

- сумма квадратов условного фактора j по i-тому количеству опытов.

Дисперсию коэффициента b₀ можно определить следующим образом:

Дисперсия коэффициента b_j может быть вычислена одним из следующих соотношений:

Дисперсия коэффициента b_uj:

Дисперсия коэффициента b_jj:

Значимость коэффициентов проверяем по критерию Стьюдента:

Коэффициент значим, если

.

f – число степеней свободы дисперсии воспроизводимости:

,

N – число опытов в эксперименте; m – число параллельных опытов.

Табличное значение определяется с помощью таблицы квантилей распределения Стьюдента при p=0.05(см. приложение). Незначимые коэффициенты можно выбросить из уравнения регрессии.

Проверим адекватность уравнения регрессии.

Адекватность уравнения проверяют по критерию Фишера:

где - остаточная дисперсия; - дисперсия воспроизводимости.

Тогда дисперсия воспроизводимости равна:

Остаточная дисперсия вычисляется следующим образом:

- экспериментальное значение, - теоретическое значение, l – число значимых коэффициентов уравнения дисперсии; N – общее количество экспериментов в одном опыте.

Табличное значение критерия Фишера определяется при уровне значимости p=0.05 и числах степеней свободы:

.

Если

,

то уравнение адекватно эксперименту.

В процессе выполнения лабораторной работы заполняем таблицу 3.1:

Таблица 3.1

Номер опыта	Экспериментальные значения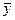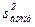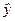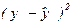
y1	y2	…	ym
…
N
Сумма столбца	-	-	-	-	-		-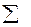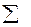

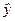- теоретическое значение (этот столбец таблицы заполняем соответствующими данными, полученными в ходе выполнения лабораторной № 2).

Пример выполнения лабораторной работы № 3.

Рассмотрим 3-факторный эксперимент (вариант 3а): N=15, число параллельных опытов m=2 (по приложению 3, таблица 3).

1. Начинаем заполнять предложенную выше таблицу 3.1:

Номер опыта	Экспериментальные значения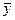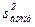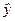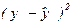
y1	y2
		70,5
		67,5
Сумма столбца	-	-	-		-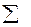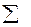

2. Найдем среднее значение отклика :

Номер опыта	Экспериментальные значения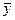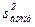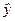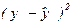
y1	y2
		70,5	70.25
			67.5
		67,5	67.25
			79.5
		66,5	66.25
Сумма столбца	-	-	-		-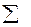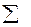

3. Определяем дисперсию воспроизводимости :

Номер опыта	Экспериментальные значения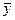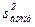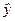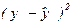
y1	y2
		70,5	70.25	0.125
			67.5	0.5
		67,5	67.25	0.125
			79.5	0.5
		66,5	66.25	0.125
Сумма столбца	-	-	-	3,375	-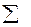

Дисперсия воспроизводимости для данного примера равна:

4. Считаем дисперсию коэффициентов.

Теперь для каждого коэффициента b_j определяем соответствующее t_j: