Методы обработки результатов измерений.
Анализ результатов любого исследования становится более убедительным и наглядным, если он соответствующим образом обработан. Разработка методов регистрации, описания и анализа результатов исследований составляет содержание специальной науки - математической статистики. Основной предпосылкой существующих методов обработки результатов является представление последних в качестве случайных величин, полученных как некоторая выборка из генеральной совокупности этих величин, под которой подразумевается все множество возможных значений этих величин.
Вычисление средних величин.
Одной из основных характеристик случайной величины является ее математическое ожидание:
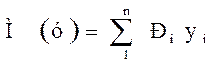 (10)
(10)
где pi - вероятность появления случайной величины у, в каждом п, измерении при их общем числе n.
При ограниченном числе измерений вместо вероятности используется частота события и вместо м(у) определяется средняя арифметическая величины у:
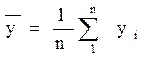 (11)
(11)
Для измерений, подчиняющихся закону нормального распределения, иногда вместо средней арифметической величины используют моду (наиболее часто встречающуюся величину) или медиану (среднюю в ранжированном ряду величин).
Конкретные величины уi будут отличаться от средней на разность 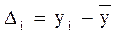 .
.
Для анализа этих отклонений используются следующие характеристики:
1) среднее арифметическое отклонение
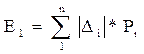 (12)
(12)
А для малого числа измерений
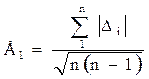 (13)
(13)
2) среднее квадратическое отклонение
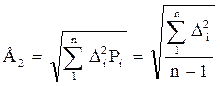 (14)
(14)
При этом, 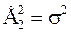 -дисперсия (математическое ожидание квадрата отклонения случайной величины от ее математического ожидания).
-дисперсия (математическое ожидание квадрата отклонения случайной величины от ее математического ожидания).
В дальнейшем мы будем обозначать дисперсию 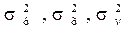 и т. п., подчеркивая, какую конкретно величину мы анализируем;
и т. п., подчеркивая, какую конкретно величину мы анализируем;
3) срединное (вероятное отклонение) е - это такая величина, относительно которой вероятность отклонений в большую и меньшую сторону одинакова и равна 0,5. Соотношения между этими отклонениями приблизительно равны:
6е ≈ 5е1 ≈4е2 (15)
Чаще других используется среднее квадратическое отклонение σу, определяющее характер разброса случайной величины, точность ее определения. Для оценки достоверности полученных результатов А. К. Митропольский [1] рекомендует использовать показатель точности исследования:
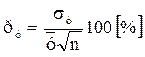 (16)
(16)
Чем точнее проведено исследование, тем меньше будет показатель рт для технических задач его желательно иметь менее 5 %.
Если известна (или задана) мера изменчивости 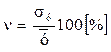 , то из формулы (16) можно получить необходимое для достоверности
, то из формулы (16) можно получить необходимое для достоверности
число экспериментов (наблюдений) n.
При прогнозировании следует знать не только конкретную
среднюю в какой-либо точке ti но и ее изменение от времени или
изменения какого-то иного фактора, то есть знать эти средние в нескольких точках.
Если линии, соединяющие указанные точки,
представляют собой ломаную, то ее следует сгладить. В ряде случаев сглаживание может облегчить применение методов выделения существующих тенденций
изменения y(t).
Один из наиболее простых приемов сглаживания [1] заключается в расчете скользящих средних, позволяющих сделать
плавными периодические и случайные колебания исследуемой величины.
Если рассматривать динамический ряд, состоящий из p уров-
ней, то скользящая средняя будет представлять собой среднюю ве-
личину для т последовательных уровней этого ряда (т < п). Для
каждого i-го уровня ряда скользящая средняя может быть вычисле-
на по формуле:
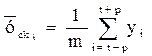 , (17)
, (17)
где 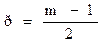
Желательно принимать m нечетным числом, тогда р = 1; 2; 3;...
Как видно, при вычислении скользящей средней теряются 1, 2, 3... Крайние точки ряда. Зато можно наглядно наблюдать существующую тенденцию изменения y(t) (рис. 1.7).
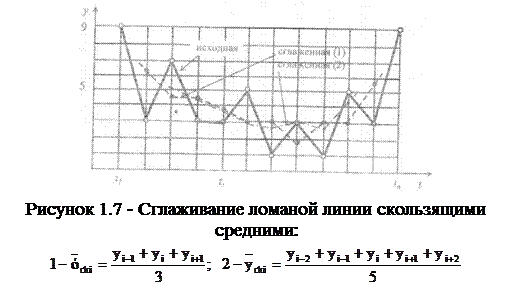
Считая, что простые скользящие средние являются весьма грубым статистическим приемом выявления тенденции, часто искажающим оценку исследуемого процесса, Е.М. Четыркин [3] рекомендует применять взвешенные скользящие средние. Под весом в
В данном случае понимается расстояние от середины интервала сглаживания. Точкам, находящимся ближе к середине конкретного интервала, приписывается больший вес. Метод определения весов, рекомендованный им, позволяет получить следующие формулы для нечетных m:
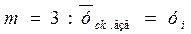 (18)
(18)
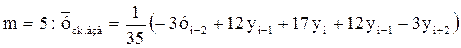 (19)
(19)
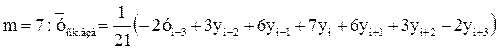 (20)
(20)
Если полученные расчетные значения 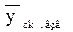 все еще обладают значительной колеблемостью, то рекомендуется повторить процесс усреднения, то есть произвести второе, а потом, может быть, и третье сглаживание.
все еще обладают значительной колеблемостью, то рекомендуется повторить процесс усреднения, то есть произвести второе, а потом, может быть, и третье сглаживание.
На наш взгляд, целесообразнее использовать в качестве коэффициентов при у известные биномиальные коэффициенты из так называемого треугольника паскаля. Тогда при нечетных m получатся следующие формулы:
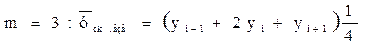 (21)
(21)
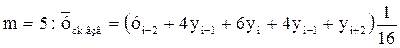 (22)
(22)
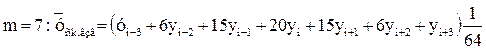 (23)
(23)
Сглаживания но этим формулам меньше искажают общую тенденцию, а мелкие волны не меняют свой знак (вместо выпуклого участка на кривой не получается вогнутый) для наглядности покажем это на рис. 1.8.
Кстати, для приведенного на рис. 1.8 примера вычисления, произведенные по формуле (19) практически совпадают с вычислениями по формуле (17) при m-3. Также близки между собой вычисления, произведенные по формулам (21) и (22). В связи с этим не всегда нужно расширять интервал сглаживания m.
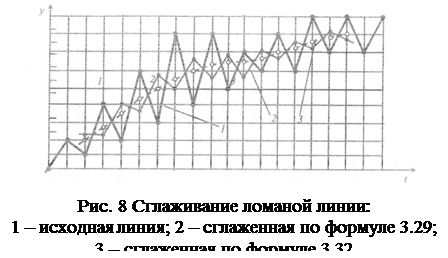

Более мягкое сглаживание по формуле (22), получается также и для ломаной с некоторой цикличностью. Пример этого показан на рис. 1.9.
Следует отметить, что сам термин "взвешенная скользящая средняя" в приведенном выше варианте соответствует одинаковому числу измерений в каждой точке ti. Более логично было бы учесть также число измерений для каждой i-й точки, особенно для технических задач. Для этого каждую величину 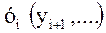 следует умножить на соответствующее число измерений
следует умножить на соответствующее число измерений 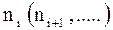 .
.
Результаты измерений 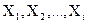 представляют собой случайные величины. Процесс обработки экспериментальных данных заключается в нахождении наивероятнейшего значения измеряемой величины (среднего арифметического
представляют собой случайные величины. Процесс обработки экспериментальных данных заключается в нахождении наивероятнейшего значения измеряемой величины (среднего арифметического 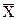 ), точности полученных результатов, средней квадратической и наибольшей возможной ошибки среднего арифметического.
), точности полученных результатов, средней квадратической и наибольшей возможной ошибки среднего арифметического.
Точность отдельного измерения определяется по формуле:
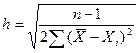
Точности среднего арифметического определяется по формуле:
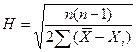 ,
,
т.е. точность среднего арифметического больше точности отдельных измерений и пропорциональна квадратному корню из числа измерений. Cредняя квадратическая ошибка 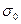 среднего арифметического определяется по формуле:
среднего арифметического определяется по формуле:
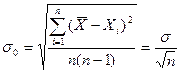 ,
,
где 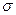 - средняя квадратическая ошибка отдельного измерения.
- средняя квадратическая ошибка отдельного измерения.
Вероятная и наибольшая возможная (при Р-0,997) ошибки среднего арифметического, соответственно, равны:
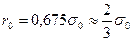 и
и 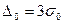
При записи среднего арифметического принято указывать его среднюю квадратическую ошибку.
Порядок выполнения работы.
1. Выберите вариант задания из таблицы случайных чисел.
2. Определите среднее арифметическое.
3. Найдите среднюю квадратическую ошибку отдельного измерения.
4. Определите наибольшую возможную ошибку 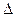 отдельного измерения и убедитесь, что среди результатов измерений нет таких, которые отличались бы от среднего арифметического более чем на
отдельного измерения и убедитесь, что среди результатов измерений нет таких, которые отличались бы от среднего арифметического более чем на 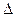 . Если бы таковые оказались, их следует отбросить и начать обработку сначала. Данные сведите в таблицу.
. Если бы таковые оказались, их следует отбросить и начать обработку сначала. Данные сведите в таблицу.
5. Определите среднюю квадратическую ошибку 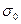 среднего арифметического.
среднего арифметического.
6. Определите характеристики 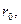
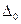 , h и H.
, h и H.
Таблица 1.2
| № | Xi | 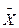 | h | H |  s0 s0 | r0 | S2 | m3 | A3 | m4 | B4 |
Контрольные вопросы.
1.Что называется случайной величиной?
2.Виды случайных величин?
3.Дискретная случайная величина? Функция распределения. Плотность распределения? Биномиальное распределение?
4.Распределение Пуассона? Нормальное распределение?
5.Вычисление средних величин?
ЛАБОРАТОРНАЯ РАБОТА №2
ПЛАНИРОВАНИЕ МНОГОФАКТОРНОГО ЭКСПЕРИМЕНТА
Цель работы.
Построение математической модели изучаемого объекта с использованием планирования эксперимента.
Основные положения.
Большое количество экспериментальных задач в химии и химической технологии формулируется как задачи экстремальные: определение оптимальных условий процесса, оптимального состава композиции и т.д. Планирование эксперимента резко повышает точность и уменьшает объем экспериментальных исследований. Поэтому использование метода планирования эксперимента является наиболее эффективным методом получения математических моделей многофакторного процесса. При его реализации можно оценить роль факторов, на которые можно воздействовать (температура, концентрации, давления и др.) при исследовании и оптимизации изучаемого объекта или технологического процесса, получить количественные оценки основных эффектов взаимодействия. Выбор плана определяется постановкой задачи исследования и особенностями объекта. Процесс исследования обычно разбивается на отдельные этапы. Информация, полученная после каждого этапа, определяет дальнейшую стратегию эксперимента. Таким образом, возникает возможность оптимального управления экспериментом. Применение методов планирования значительно повышает эффективность эксперимента [1].
Рассмотрим основные определения, сущность и задачи планирования эксперимента; порядок построения модели исследуемого процесса при помощи полного факторного эксперимента, особенности построения моделей с учетом нелинейностей типа квадрата факторов, а также расчетные формулы для обработки и оценки экспериментальных данных.
Переменные x1, x2, …, xk принято называть факторами. Факторами могут быть какие-либо внешние для объекта исследования воздействия (влажность, температура окружающей среды), или же параметры самого объекта (концентрация, температура, давление, удельная теплоемкость рабочей смеси). Выходные параметры также могут быть разнородными. В зависимости от решаемой задачи выходная величина называется откликом, функцией цели, функцией отклика, параметром оптимизации. Обычно аналитическая связь между входом и выходом (модель объекта) неизвестна, а известны факторы xi и подлежащие исследованию выходные величины yi.
Область определения двух факторов x1, x2 называется двухфакторным пространством, а эксперимент – двухфакторным экспериментом.
Каждый фактор может принимать определенное количество значений. Эти значения называются уровнями факторов. Например, если факторы могут принимать два значения -1, +1, то число уровней равно 2.
Число опытов в одном эксперименте равно числу различных наборов факторов. Для полного факторного эксперимента необходимое количество опытов N определяется по формуле:
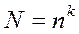 ,
,
где n – количество уровней; k – число факторов.
При проведении двухфакторного эксперимента на двух уровнях результат эксперимента представляет собой квадрат и число опытов равно:
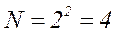 .
.
При проведении трехфакторного эксперимента на двух уровнях результат эксперимента представляет собой куб или параллелепипед, число вершин которого равно числу опытов:
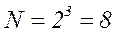 .
.
Выбор факторов.
Приступая к планированию эксперимента, необходимо выбрать факторы и определить: влияние их на выходную величину y, какие из них могут задаваться по желанию экспериментатора, какие неуправляемы или случайны, являются ли факторы зависимыми или независимыми величинами [2].
Для каждого эксперимента необходимо выбрать интервал варьирования факторов h. Данным фактором называется половина разности между верхним и нижним значением:
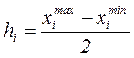
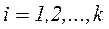 .
.
Интервал варьирования физического фактора должен быть таким, чтобы его величина примерно на порядок превосходила погрешность установки и измерения величины xi; аппроксимирующая функция незначительно отличалась от искомой зависимости – требование адекватности модели; при переходе от одного опыта к другому изменение отклика было достаточно ощутимым, т.е. в несколько раз превосходило погрешность отклика.
Значение фактора в центре области эксперимента называется его основным уровнем или центром плана, обозначается 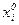 и может быть найдено следующим образом:
и может быть найдено следующим образом:
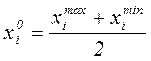
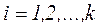 .
.
Для удобства записи плана эксперимента и обработки экспериментальных данных обычно пользуются условными значениями факторов, которые обозначаются 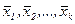 и вычисляются по формуле:
и вычисляются по формуле:
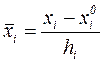
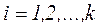 .
.
Данная процедура равносильна переносу начала координат в точку основного уровня факторов и изменению масштаба. Все условные факторы – безразмерные и нормированные величины.
Модель процесса.
Выбор модели (уравнения модели) в методе планирования эксперимента – неформализованный этап, который основывается обычно на интуитивных соображениях с учетом предыдущего опыта экспериментатора, а количественное определение коэффициентов выбранных уравнений модели – на результатах эксперимента. Поэтому правильный выбор модели должен подтверждаться экспериментально.
Модель определяется переменными xi и постоянными параметрами βi и в общем случае имеет вид:
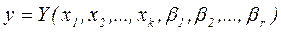 .
.
Модели могут быть линейные относительно xi:
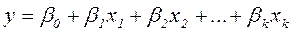 ,
,
Также они могут быть нелинейного вида:
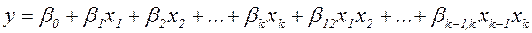
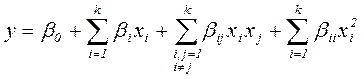
Построение планов полного факторного эксперимента.
Полным факторным называется такой эксперимент, в котором реализуются все возможные комбинации (наборы) уровней факторов [3]. Если k факторов варьируются на двух уровнях, то число всех возможных наборов – N=2k. Если k факторов варьируются на трех уровнях, то N=3k. С увеличением числа факторов k, быстро растет число опытов.
Используя полученные данные можно представить план эксперимента в виде таблицы матрицы. Для двухфакторного эксперимента:
| Номер опыта | Уровни переменных | Отклики | |||
| x1 | x2 | yu1 | yu2 | yuj | |
| -1 | -1 | y11 | y12 | y1j | |
| +1 | -1 | y21 | y22 | y2j | |
| -1 | +1 | y31 | y32 | y3j | |
| +1 | +1 | y41 | y42 | y4j |
Для трехфакторного эксперимента:
| Номер опыта | Уровни переменных | Отклики | ||||
| x1 | x2 | x3 | yu1 | yu2 | yuj | |
| -1 | -1 | -1 | y11 | y12 | y1j | |
| +1 | -1 | -1 | y21 | y22 | y2j | |
| -1 | +1 | -1 | y31 | y32 | y3j | |
| +1 | +1 | -1 | y41 | y42 | y4j | |
| -1 | -1 | +1 | y51 | y52 | y5j | |
| +1 | -1 | +1 | y61 | y62 | y6j | |
| -1 | +1 | +1 | y71 | y72 | y7j | |
| +1 | +1 | +1 | y81 | y82 | y8j |
В каждой точке может проводиться несколько опытов nu, которые называются параллельными. Для проведения эксперимента значения факторов разделяются на уровни, задаваемые соответствующими строками.
Основные достоинства планов ПФЭ – простота определения коэффициентов уравнения регрессии, возможность учета произведений взаимодействия факторов без изменения плана основного эксперимента. Преимущества любой матрицы ПФЭ достигаются за счет особого построения плана эксперимента, при котором матрица обладает свойствами ортогональности, нормировки, симметрии и ротатабельности [3].
Свойство ортогональности: сумма построчных произведений элементов любых двух граф равно нулю.
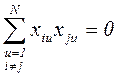
где i, j – номер столбца или номер фактора; i=1,2,…, k (k – общее количество факторов); u – номер набора факторов или номер строки; N – общее число различных наборов или число строк матрицы ПФЭ.
Свойство нормировки: сумма квадратов элементов любой графы равна числу различных опытов – строк N.
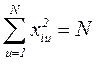
Свойство симметрии: алгебраическая сумма элементов любого реального фактора равна нулю (условие баланса положительных и отрицательных значений каждой переменной).
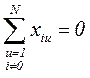
Свойство ротатабельности: дисперсии предсказанных значений отклика на равных расстояниях от центра плана постоянны и минимальны.
В полном факторном эксперименте возможен учет нелинейностей типа произведения факторов (уравнение регрессии отличается от линейного наличием слагаемого xixj) и учет нелинейностей типа квадратов факторов.
План, учитывающий нелинейности типа квадратов факторов, называется ортогональным центрально-композиционным планом (ОЦКП) второго порядка. Они позволяют сформировать функцию отклика в виде полного квадратичного полинома, который содержит большее число членов, чем неполный квадратичный полином, сформированный по планам первого порядка, и поэтому требуют большего числа выполняемых опытов.
В общем случае для k факторов полином второй степени имеет вид:
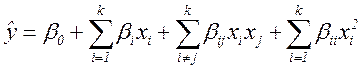
Полный квадратичный полином при k=2 содержит 6 членов и имеет вид:
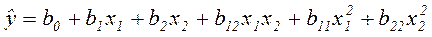
при k=3 – 11 членов:
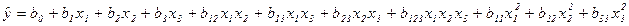 Для получения квадратичной зависимости каждый фактор должен фиксироваться как минимум на трех уровнях.
Для получения квадратичной зависимости каждый фактор должен фиксироваться как минимум на трех уровнях.
Планы ПФЭ не позволяют найти коэффициенты βii при квадратах факторов, так как все графы 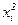 тождественны графе x0 (xi=±1,
тождественны графе x0 (xi=±1, 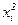 =1). Кроме того, для этих граф нарушаются условия ортогональности и симметричности. В основе построения планов второго порядка, как и планов первого порядка, лежат принципы ортогональности граф и их симметрия. Условие нормировки может не выполняться.
=1). Кроме того, для этих граф нарушаются условия ортогональности и симметричности. В основе построения планов второго порядка, как и планов первого порядка, лежат принципы ортогональности граф и их симметрия. Условие нормировки может не выполняться.
Для выполнения этих принципов к центру плана второго порядка, ядру – 2k добавляются дополнительные точки факторного пространства. Точки называются звездными. Положение звездных точек определяется из условия ортогональности всех граф матрицы планирования второго порядка. Кроме значений факторов на уровнях ±1, в плане добавляется точка начала координат xi=0 (i=1, 2,…,k), и на каждой координате выбираются две звездные точки xi=α.
Общее число опытов определяется соотношением:
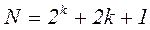
k – количество факторов.
На рисунке 2.1 показано проведение опыта в двухфакторном пространстве для плана ОЦКП. Звездные точки отмечены кружками. Величина α называется плечом звездных точекили звездным плечом. Положение звездных точек зависит от числа варьируемых факторов.
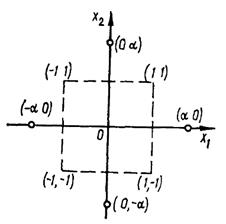
Рисунок 2.1 – расположение звездных точек.
Наличие звездных точек обеспечивает ортогональность граф первых степеней факторов. В ОЦКП каждый фактор фиксируется, в общем случае на пяти уровнях – -α, -1, 0, 1, α.
Для обеспечения ортогональности всех граф матрицы ОЦКП необходимо преобразовать квадраты факторов по формуле:
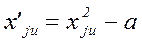
Значение поправки a определяется следующим образом. Сумма элементов столбца, соответствующего квадратам факторов, должна быть равна нулю:
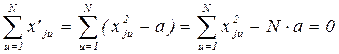
Откуда
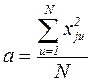 (2.1)
(2.1)
В общем случае ортогональный центрально-композиционный план при трех факторах имеет вид, представленный в таблице 2.1.
Таблица 2.1
| Но-мер опы-та | x0 | x1 | x2 | x3 | x1∙x2 | x1∙x3 | x2∙x3 | x1∙x2∙x3 | 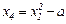 | 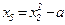 | 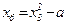 | y | |
| Точки плана ПФЭ 23 (N0=2k точек) | +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | 1-a | 1-a | 1-a | y1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | 1-a | 1-a | 1-a | y2 | ||
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | 1-a | 1-a | 1-a | y3 | ||
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | 1-a | 1-a | 1-a | y4 | ||
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | 1-a | 1-a | 1-a | y5 | ||
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | 1-a | 1-a | 1-a | y6 | ||
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | 1-a | 1-a | 1-a | y7 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | 1-a | 1-a | 1-a | y8 | ||
| Звездные точки (2k точек) | +1 | -α | α2-a | -a | -a | y9 | |||||||
| +1 | + α | α2-a | -a | -a | y10 | ||||||||
| +1 | - α | -a | α2-a | -a | y11 | ||||||||
| +1 | + α | -a | α2-a | -a | y12 | ||||||||
| +1 | - α | -a | -a | α2-a | y13 | ||||||||
| +1 | + α | -a | -a | α2-a | y14 | ||||||||
| Нулевая точка | +1 | -a | -a | -a | y15 | ||||||||
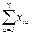 | - | N | - | ||||||||||
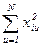 | - | N | 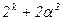 | 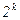 | 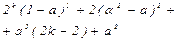 |
Для определения неизвестных a и α нужно сформировать и решить систему из двух уравнений. Одно из них для a было записано раннее – это уравнение (2.1). Другое уравнение получим из условия ортогональности для столбцов x4 и x5:
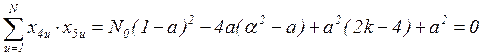 .
.
После простейших преобразований с учетом того, что 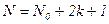 - общее число опытов в плане, получаем:
- общее число опытов в плане, получаем:
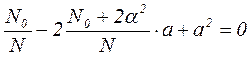 .
.
Соотношение для a при j=1, 2 или 3 может быть записано как (см. таблицу 2.1):
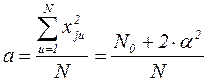 .
.
Подставив его в предыдущее уравнение, получаем:
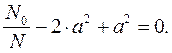
Откуда
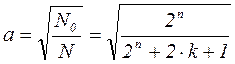 .
.
Тогда
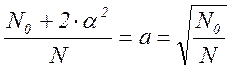 .
.
И плечо звездных точек
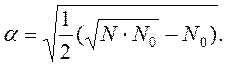
Например, для ОЦКП при числе факторов k=3 параметры плана следующие:
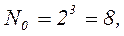
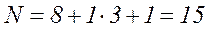
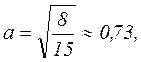
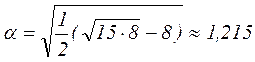
Обобщим результаты в таблицу 2.2.
Таблица 2.2
| Число факторов k | Ядро (центр) плана | Общее число опытов N | Звездное плечо α | Значение поправки a |
| 22 | 1.0000 | 2/3=0.6667 | ||
| 23 | 1.2154 | 8/15=0.7303 | ||
| 24 | 1.4142 | 4/5=0.80 | ||
| 25-1 | 1.5467 | 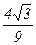 =0.7698 =0.7698 | ||
| 25 | 1.5960 | 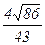 =0.8627 =0.8627 |
Располагая данными таблицы 2.2, можно построить ортогональные центрально-композиционные планы второго порядка.
По результатам опытов формируется полином.
при k=2:
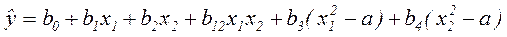
при k=3:
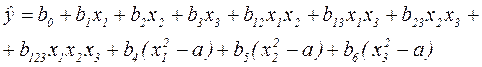
Коэффициенты полинома определяются по формуле:
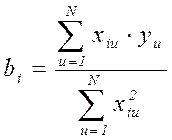
Полиномы можно представить в виде:
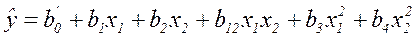 - при k=2;
- при k=2;
и при k=3:
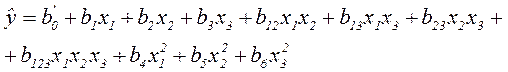
Где коэффициент 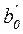 определяется следующим образом при k=2:
определяется следующим образом при k=2:
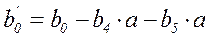
при k=3:
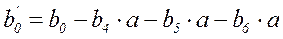
Ортогональные центрально композиционные планы при 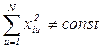 не обеспечивают постоянства дисперсии отклика в различных точках факторного пространства.
не обеспечивают постоянства дисперсии отклика в различных точках факторного пространства.
Порядок выполнения работы.
1. Выберете вариант задания из приложения 3. В соответствии с заданием выполните следующие пункты.
2. Оцениваем граничные значения факторов, центр плана, шаг варьирования.
Шаг варьирования:
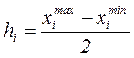
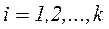 ,
,
где 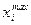 - верхнее граничное значение фактора;
- верхнее граничное значение фактора; 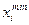 - нижнее граничное значение фактора.
- нижнее граничное значение фактора.
Значение фактора в центре области эксперимента называется его основным уровнем или центром плана, обозначается 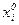 и может быть найдено следующим образом:
и может быть найдено следующим образом:
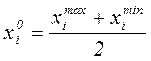
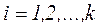
Граничные значения:
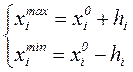
3. Переводим все значения факторов в условные единицы по формуле:
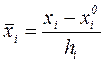
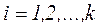 ,
,
где 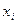 - значения фактора в натуральном масштабе,
- значения фактора в натуральном масштабе, 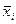 - значение фактора в условном масштабе.
- значение фактора в условном масштабе.
Для граничных условий и центра плана:
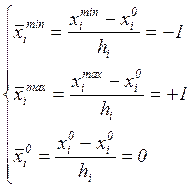
Результаты пересчета значений факторов из натуральных величин в условные сведем в таблицу 2.3:
Таблица 2.3
| № | Фактор | Основной уровень (в натуральных единицах) | Шаг варьирования (в натуральных единицах) | Значения уровней переменных соответствующие условным единицам | ||
| -1 | +1 | |||||
| 1. | ||||||
| 2. | ||||||
| 3. |
Построим ортогональный центрально-композиционный план (ОЦКП) второго порядка, который учитывает нелинейности типа квадрата факторов.
Схема планирования 2-факторного эксперимента
Полный квадратичный полином при k=2 содержит 6 членов и имеет вид:
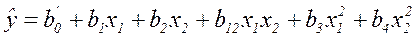
Общее число опытов вычисляется по формуле:
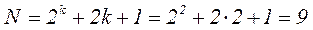
Звездное плечо:
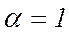
Значение поправки a:
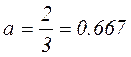
Все данные берем из таблицы, расположенной в пункте «Основные положения» в соответствии со значением k.
Значит, квадраты факторов преобразуются по формуле:
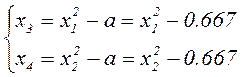
Значение коэффициентов уравнения вычисляются следующим образом:
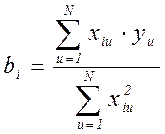
где yu – экспериментальное значение соответствующего опыта.
Коэффициент 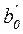 :
:
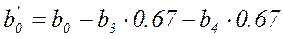
Заполняем таблицу 2.4.
4.1. Считаем столбцы 5-14. Столбец 8 – экспериментальные данные, их заполняем из таблицы приложения в соответствии с вариантом.
4.2. Вычисляем коэффициенты bi по соответствующей формуле, приведенной выше. Коэффициент b1, к примеру, считается так:
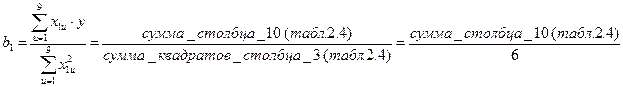
4.3. Составляем уравнение регрессии.
4.4. В полученное уравнение регрессии подставляем значения факторов в условных единицах. Таким образом, заполняем столбец 15.
4.5. Определяем отклонение расчетного значения 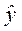 от экспериментального y – заполняем столбец 16.
от экспериментального y – заполняем столбец 16.
В конце расчета каждого столбца не забываем определять сумму столбца, если стоит знак 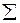 , или сумму квадратов элементов столбца если стоит
, или сумму квадратов элементов столбца если стоит 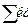 .
.
Таблица 2.4
| Но- мер опы- та | x0 | x1 | x2 | x1·x2 | 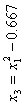 | 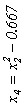 | y | x0·y | x1·y | x2·y | x1·x2·y | x3·y | x4·y | 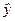 | 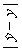 |
| +1 | -1 | -1 | |||||||||||||
| +1 | +1 | -1 | |||||||||||||
| +1 | -1 | +1 | |||||||||||||
| +1 | +1 | +1 | |||||||||||||
| +1 | -1 | ||||||||||||||
| +1 | +1 | ||||||||||||||
| +1 | -1 | ||||||||||||||
| +1 | +1 | ||||||||||||||
| +1 | |||||||||||||||
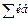 | 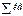 | 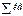 | 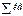 | 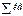 | 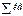 | - | 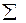 | 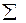 | 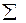 | 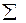 | 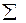 | 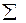 | - | - | |
| - | - | - | |||||||||||||
Наши рекомендации
|
