Аналитические методы расчета
Исследования общих свойств нелинейных цепей удобно осуществлять на основе математического анализа, базирующегося на аналитическом выражении характеристик нелинейных элементов, т.е. их аппроксимации. На выбор аналитического метода влияют условия поставленной задачи, а также характер возможного перемещения рабочей точки по характеристике нелинейного элемента: по всей характеристике или в ее относительно небольшой области.
К аналитическим методам относятся:
- метод аналитической аппроксимации;
- метод кусочно-линейной аппроксимации;
- метод линеаризации.
Метод аналитической аппроксимацииоснован на замене характеристики (или ее участка) нелинейного элемента общим аналитическим выражением. Применяются следующие виды аналитической аппроксимации:
- степенным многочленом (см. рис. 2,а);
- трансцендентными (экспоненциальными, гиперболическими и др.) функциями (см. рис. 2,б).
Выбор коэффициентов (а,b,c,…) осуществляется исходя из наибольшего соответствия аналитического выражения рабочему участку нелинейной характеристики. При этом
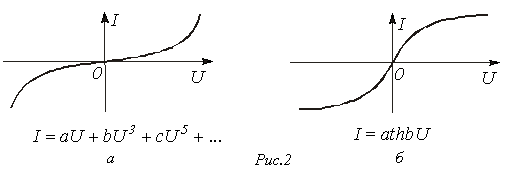
выбираются наиболее характерные точки, через которые должна пройти аналитическая кривая. Число точек равно числу коэффициентов в аналитическом выражении, что позволяет однозначно определить последнее.
Необходимо помнить, что при получении нескольких корней нелинейного уравнения они должны быть проверены на удовлетворение задаче. Пусть, например, в цепи, состоящей из последовательно соединенных линейного R и нелинейного резисторов, ВАХ последнего может быть аппроксимирована выражением 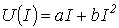 . Определить ток в цепи, если источник ЭДС Е обеспечивает режим работы цепи в первом квадранте.
. Определить ток в цепи, если источник ЭДС Е обеспечивает режим работы цепи в первом квадранте.
В соответствии со вторым законом Кирхгофа для данной цепи имеет место уравнение
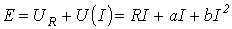
или
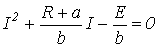 .
.
Корни уравнения
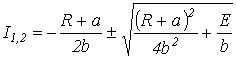 .
.
Решением задачи является 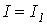 , поскольку второе решение
, поскольку второе решение 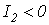 не удовлетворяет условиям исходя из физических соображений.
не удовлетворяет условиям исходя из физических соображений.
Метод кусочно-линейной аппроксимацииоснован на представлении характеристики нелинейного элемента отрезками прямых линий (см. рис. 3), в результате чего нелинейная цепь может быть описана линейными уравнениями с постоянными (в пределах каждого отрезка) коэффициентами.
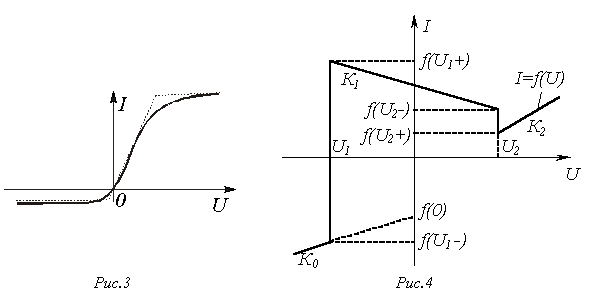
При наличии в цепи двух и более нелинейных резисторов реализация метода затруднена, так как в общем случае изначально неизвестно, на каких участках ломаных кривых находятся рабочие точки.
Кусочно-линейная аппроксимация может быть реализована методом секционных кусочно-линейных функций,позволяющим описать ломаную кривую общим аналитическим выражением. Например, для кривой, представленной на рис. 4 и определяемой коэффициентами 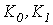 и
и 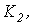 характеризующими наклон ее отдельных прямолинейных участков, и параметрами
характеризующими наклон ее отдельных прямолинейных участков, и параметрами 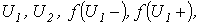
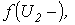
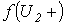 , характеризующими координаты точек, где значения функции изменяются скачками, данное выражение будет иметь вид
, характеризующими координаты точек, где значения функции изменяются скачками, данное выражение будет иметь вид
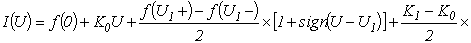
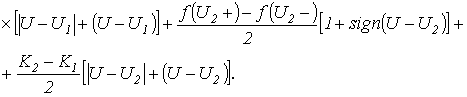
Здесь два первых слагаемых в правой части определяют первый наклонный участок аппроксимируемой кривой; три первых слагаемых - первый наклонный участок и участок первого скачка; четыре первых слагаемых - первый и второй наклонные участки с учетом участка первого скачка и т.д.
В общем случае аппроксимирующее выражение по методу секционных кусочно - линейных функций имеет вид
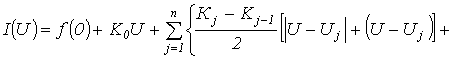
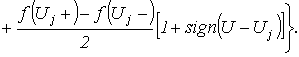
Метод линеаризацииприменим для анализа нелинейных цепей при малых отклонениях рабочей точки Р (см. рис. 5) от исходного состояния.
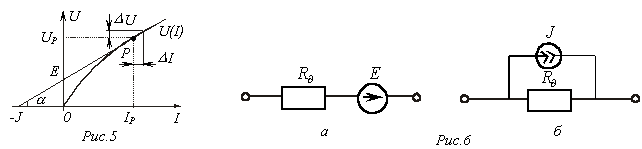
В окрестности рабочей точки 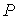 (см. рис. 5)
(см. рис. 5)
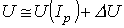 ,
,
где 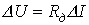 (закон Ома для малых приращений);
(закон Ома для малых приращений);
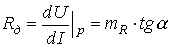 -дифференциальное сопротивление.
-дифференциальное сопротивление.
Идея метода заключается в замене нелинейного резистора линейным с сопротивлением, равным дифференциальному в заданной (или предполагаемой) рабочей точке, и либо последовательно включенным с ним источником ЭДС, либо параллельно включенным источником тока. Таким образом, линеаризованной ВАХ (см. прямую на рис. 5) соответствует последовательная (рис. 6,а) или параллельная (рис. 6,б) схема замещения нелинейного резистора.
Если исходный режим определен и требуется рассчитать лишь приращения токов и (или) напряжений, обусловленные изменением напряжения или тока источника, целесообразно использовать эквивалентные схемы для приращений,получаемые на основании законов Кирхгофа для малых приращений:
-первый закон Кирхгофа: 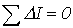 ;
;
-второй закон Кирхгофа: 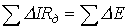 .
.
При составлении схемы для приращений:
1) все ЭДС и токи источников заменяются их приращениями;
2) нелинейные резисторы заменяются линейными с сопротивлениями, равными дифференциальным в рабочих точках.
Необходимо помнить, что полная величина какого-либо тока или напряжения в цепи равна алгебраической сумме исходного значения переменной и ее приращения, рассчитанного методом линеаризации.
Если исходный режим работы нелинейного резистора неизвестен, то следует задаться рабочей точкой на его ВАХ и, осуществив соответствующую линеаризацию, произвести расчет, по окончании которого необходимо проверить, соответствуют ли его результаты выбранной точке. В случае их несовпадения линеаризованный участок уточняется, расчет повторяется и так до получения требуемой сходимости
Итерационные методы расчета
Решение нелинейного уравнения (системы нелинейных уравнений), описывающего (описывающих) состояние электрической цепи, может быть реализовано приближенными численными методами. Решение находится следующим образом: на основе первой, достаточно грубой, оценки определяется начальное значение корня (корней), после чего производится уточнение по выбранному алгоритму до вхождения в область заданной погрешности.
Наиболее широкое применение в электротехнике для численного расчета нелинейных резистивных цепей получили метод простой итерации и метод Ньютона-Рафсона, основные сведения о которых приведены в табл. 1.
Таблица 1. Итерационные методы расчета
| Последователь-ность расчета | Геометрическая иллюстрация алгоритма | Условие сходимости итерации | Примечание |
Метод простой итерации 1.Исходное нелинейное уравнение электрической цепи 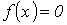 , где , где 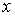 -искомая переменная, представляется в виде -искомая переменная, представляется в виде 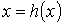 . 2. Производится расчет по алгоритму . 2. Производится расчет по алгоритму 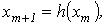 где где 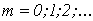 - шаг итерации. - шаг итерации. | 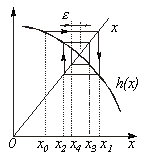 Здесь Здесь 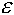 - заданная погрешность - заданная погрешность | На интервале между приближенным и точным значениями корня должно выполняться неравенство 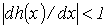 | 1.Начальное приближение 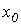 обычно находится из уравнения обычно находится из уравнения 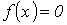 при пренебрежении в нем нелинейными членами. 2. Метод распространим на систему нелинейных уравнений n-го порядка. Например, при решении системы 2-го порядка при пренебрежении в нем нелинейными членами. 2. Метод распространим на систему нелинейных уравнений n-го порядка. Например, при решении системы 2-го порядка 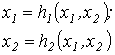 итерационные формулы имеют вид итерационные формулы имеют вид 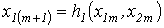 ; ; 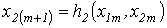 . 3. При решении системы уравнений сходимость обычно проверяется в процессе итерации. . 3. При решении системы уравнений сходимость обычно проверяется в процессе итерации. |
Метод Ньютона- -Рафсона 1. На основании исходного нелинейного уравнения электрической цепи 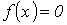 , где , где 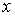 -искомая переменная, записывается итерационная формула -искомая переменная, записывается итерационная формула 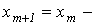 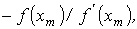 где где 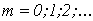 - шаг итерации. 2.По полученной формуле проводится итерационный расчет - шаг итерации. 2.По полученной формуле проводится итерационный расчет | 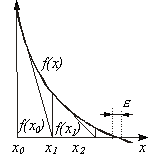 Здесь Здесь 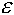 - заданная погрешность - заданная погрешность | На интервале между приближенным и точным значениями корня должны выполняться неравенства 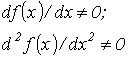 | Примечания п. 1,2 и 3 к методу простой итерации распространимы на метод Ньютона-Рафсона. При этом при решении системы 2-го порядка 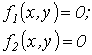 итерационные формулы имеют вид итерационные формулы имеют вид 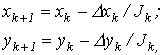 где где  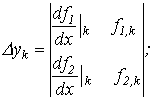 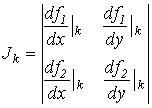 |
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.: Энергия- 1972. –200с.
- Матханов П.Н.Основы анализа электрических цепей. Нелинейные цепи.: Учеб. для студ. электротехн. спец. вузов. 2-е изд., переработ. и доп. –М.: Высш. шк., 1986. –352с.
- Чуа Л.О., Лин Пен-Мин.Машинный анализ электронных схем: алгоритмы и вычислительные методы: Пер. с англ. –М.: Энергия, 1980. – 640 с.
- Сборник задач и упражнений по теоретически основам электротехники: Учеб. пособие для вузов /Под ред. проф. П.А.Ионкина. –М.: Энергоиздат, 1982. –768 с.
Контрольные вопросы и задачи
- Как рассчитываются цепи с одним нелинейным резистором и произвольным числом линейных?
- В чем преимущества и недостатки аналитических методов расчета по сравнению с графическими?
- Какие аналитические методы используются для расчета нелинейных резистивных цепей постоянного тока?
- В чем сущность метода линеаризации? Для решения каких двух типов задач он применяется?
- Что такое эквивалентные схемы для приращений? Как они составляются?
- Какова последовательность расчета нелинейных цепей итерационными методами?
- В диагонали моста находится нелинейный резистор, ВАХ которого аппроксимирована выражением
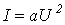 , где
, где 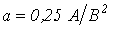 . Линейные сопротивления противоположных плеч моста попарно равны:
. Линейные сопротивления противоположных плеч моста попарно равны: 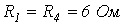 ;
; 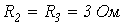 . Определить мощность, рассеиваемую нелинейным резистором, если схема питается от источника с ЭДС
. Определить мощность, рассеиваемую нелинейным резистором, если схема питается от источника с ЭДС 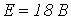 .
.
Ответ: Р=2 Вт.
- Определить ток в цепи, состоящей из последовательно соединенных линейного
 и нелинейного резисторов, если кривая ВАХ последнего
и нелинейного резисторов, если кривая ВАХ последнего 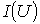 проходит через точки с координатами (15 В; 1,425 А) и (5 В; 0,325 А) и аппроксимирована выражением вида
проходит через точки с координатами (15 В; 1,425 А) и (5 В; 0,325 А) и аппроксимирована выражением вида  . ЭДС на входе цепи
. ЭДС на входе цепи 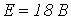 .
.
Ответ: 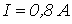 .
.
- В схеме предыдущей задачи ВАХ нелинейного резистора описывается выражением (ток – в амперах, напряжение – в вольтах)
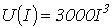 ;
; 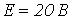 ;
;  . Определить напряжение
. Определить напряжение 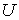 на нелинейном резисторе и ток
на нелинейном резисторе и ток 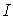 в нем методом Ньютона-Рафсона.
в нем методом Ньютона-Рафсона.
Ответ: 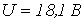 ;
; 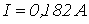 .
.
- В цепи на рис. 1,б
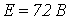 ,
, 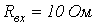 . ВАХ нелинейного резистора аппроксимирована двумя прямолинейными отрезками, первый из которых проходит через точки с координатами (0 В; 0 А) и (9 В; 2 А), а второй – через точки с координатами (9 В; 2 А) и (12 В; 6 А). Определить ток в цепи.
. ВАХ нелинейного резистора аппроксимирована двумя прямолинейными отрезками, первый из которых проходит через точки с координатами (0 В; 0 А) и (9 В; 2 А), а второй – через точки с координатами (9 В; 2 А) и (12 В; 6 А). Определить ток в цепи.
Ответ: 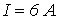 .
.
Лекция N 32
Нелинейные магнитные цепи при постоянных потоках.
Основные понятия и законы магнитных цепей

При решении электротехнических задач все вещества в магнитном отношении делятся на две группы:
- ферромагнитные(относительная магнитная проницаемость
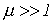 );
); - неферромагнитные(относительная магнитная проницаемость
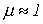 ).
).
Для концентрации магнитного поля и придания ему желаемой конфигурации отдельные части электротехнических устройств выполняются из ферромагнитных материалов. Эти части называют магнитопроводами или сердечниками.Магнитный поток создается токами, протекающими по обмоткам электротехнических устройств, реже – постоянными магнитами. Совокупность устройств, содержащих ферромагнитные тела и образующих замкнутую цепь, вдоль которой замыкаются линии магнитной индукции, называют магнитной цепью.
Магнитное поле характеризуется тремя векторными величинами, которые приведены в табл. 1.
Таблица 1. Векторные величины, характеризующие магнитное поле
| Наименование | Обозначение | Единицы измерения | Определение |
| Вектор магнитной индукции | 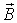 | Тл (тесла) | Векторная величина, характеризующая силовое действие магнитного поля на ток по закону Ампера |
| Вектор намагниченности | 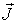 | А/м | Магнитный момент единицы объема вещества |
| Вектор напряженности магнитного поля | 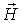 | А/м |   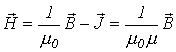 , где , где 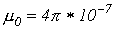  Гн/м- магнитная постоянная Гн/м- магнитная постоянная |
Основные скалярные величины, используемые при расчете магнитных цепей, приведены в табл. 2.
Таблица 2. Основные скалярные величины, характеризующие магнитную цепь
| Наименование | Обозначение | Единица измерения | Определение |
| Магнитный поток | 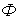 | Вб (вебер) | Поток вектора магнитной индукции через поперечное сечение 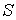 магнитопровода магнитопровода 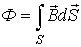 |
| Магнитодвижущая (намагничивающая) сила МДС (НС) | 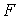 | A | 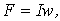 где где 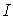 -ток в обмотке, -ток в обмотке, 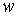 -число витков обмотки -число витков обмотки |
| Магнитное напряжение | 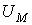 | А | Линейный интеграл от напряженности магнитного поля 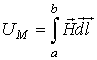 , где , где 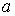 и и 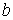 -граничные точки участка магнитной цепи, для которого определяется -граничные точки участка магнитной цепи, для которого определяется 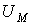 |
