Корни характеристического уравнения. Постоянная времени
Выражение свободной составляющей 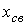 общего решения х дифференциального уравнения (2) определяется видом корней характеристического уравнения (см. табл. 3).
общего решения х дифференциального уравнения (2) определяется видом корней характеристического уравнения (см. табл. 3).
Таблица 3. Выражения свободных составляющих общего решения
| Вид корней характеристического уравнения | Выражение свободной составляющей |
Корни 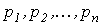 вещественные и различные вещественные и различные | 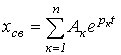 |
Корни 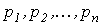 вещественные и вещественные и 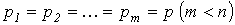 | 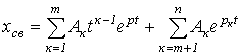 |
Пары комплексно-сопряженных корней 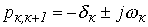 | 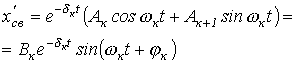 |
Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.
При вещественных корнях 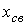 монотонно затухает, и имеет место апериодический переходный процесс.Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).
монотонно затухает, и имеет место апериодический переходный процесс.Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).
Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением
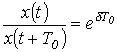 ,
,
которое называетсядекрементом колебания,или натуральным логарифмом этого отношения
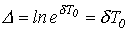 ,
,
называемым логарифмическим декрементом колебания, где 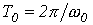 .
.
Важной характеристикой при исследовании переходных процессов является постоянная времени t, определяемая для цепей первого порядка, как:
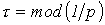 ,
,
где р – корень характеристического уравнения.
Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при 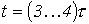
.
Литература
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- Чем обусловлены переходные процессы?
- Как определяется порядок дифференциального уравнения, описывающего переходный процесс?
- Для каких цепей применим классический метод расчета переходных процессов?
- Доказать законы коммутации:
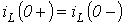 и
и 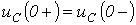 - с энергетических позиций.
- с энергетических позиций. - В каких цепях и почему возможен колебательный процесс?
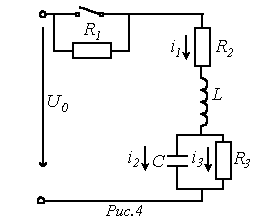
- Определить величину токов
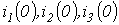 и напряжений
и напряжений 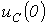 на конденсаторе и
на конденсаторе и 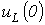 на катушке индуктивности в момент коммутации в цепи на рис. 4, если
на катушке индуктивности в момент коммутации в цепи на рис. 4, если 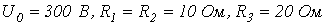 .
.
 | Ответ: 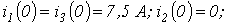 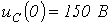 ; ; 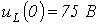 . . |
Лекция N 25
