Итак, функция равномерного распределения задается формулой

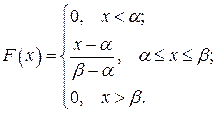
и ее график изображен на рис. 2.15.

Определим основные числовые характеристики случайной величины Х , подчиненной закону равномерной плотности на промежутке от α до β . Математическое ожидание

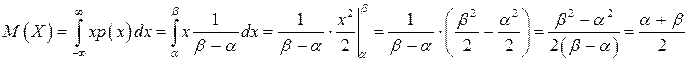
В силу симметричности равномерного распределения медиана величины Х равна 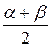, моды нет.

Дисперсия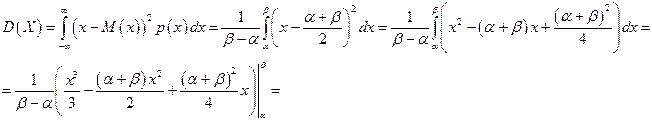

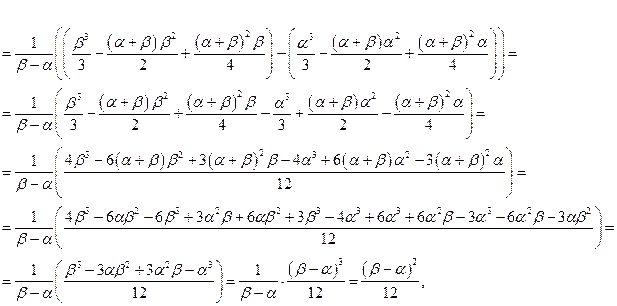
откуда среднее квадратическое отклонение 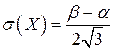. В силу симметричности распределения его асимметрия равна нулю: .

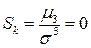Равномерное распределение имеют случайные величины, характеризующие ошибки измерений при помощи инструмента с крупными делениями, когда значение округляется до ближайшего целого. Например, равномерное распределение имеет ошибка указания времени часами со скачущей стрелкой.

Пример 2.16. Перекресток оборудован автоматическим светофором, в котором зеленый и красный свет горит в течение 1 мин и 0,5мин соответственно. Водитель подъезжает к перекрестку в случайный момент времени, не связанный с работой светофора. Найти вероятность того, что он проедет перекресток не останавливаясь.

Решение. Случайная величина Х, обозначающая момент проезда автомашины через перекресток, распределена равномерно в интервале, равном периодусмены цветов в светофоре, т.е. в интервале (0; 1,5). Тогда плотность распределения будет иметь вид:

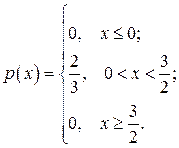
Для того чтобы автолюбитель проехал перекресток не останавливаясь, нужно, чтобы момент проезда перекрестка пришелся на интервал времени (0; 1). Для случайной величины, распределенной равномерно в интервале (0; 1,5), вероятность того, что она примет значениеиз интервала (0; 1) вычислим по формуле:

.

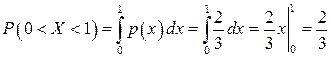Ответ:вероятность того, что водитель проедет перекресток не останавливаясь, равна .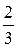

Нормальное распределение. Закон нормального распределения получен в связи с разработкой теории ошибок наблюдения. Случайные ошибки измерений складываются из множества различных неконтролируемых причин: температурных колебаний, вибраций в окружающей среде, неточностью измерительной шкалы прибора и т. д. Если каждая из этих случайных причин

оказывает на результаты измерений незначительное влияние по сравнению с общим эффектом, тоих сумма (случайная ошибка) подчинена закону, близкому к нормальному (для появления нормального распределения необходимо выполнение дополнительных условий). Например, рост большого числа лиц одного и же пола, национальности и возраста, размеры органов животных также подчиняются нормальному распределению.

Нормальный закон распределения характеризуется плотностью вероятности вида

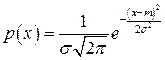(2.18)

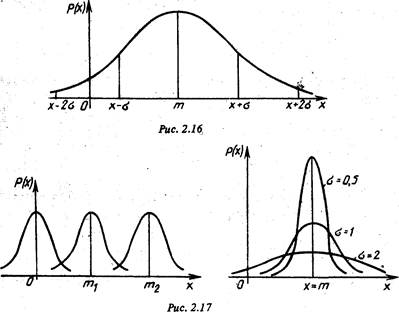
Кривая распределения – это кривая Гаусса, которая имеет симметричный холмообразный вид (рис. 2.16). Из формулы (2.18) следует, что кривая у = р(х) достигает максимума 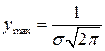при х = т. С ростом 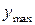уменьшается, а так как площадь, ограниченная всей кривой и осью Ох, равна1, то с увеличением кривая как бы растягивается вдоль оси Ох. При уменьшении кривая вытягивается вверх вдоль прямой х = т, но сжимается в горизонтальном направлении. Если же зафиксировать , а изменять т, то кривая будет смещаться в горизонтальном направлении, сохраняя форму.

Следовательно, параметр характеризует форму кривой, а т – ее положение (рис. 2.17).

Найдем функцию распределения F(х) случайной величины Х, распределенной по нормальному закону:

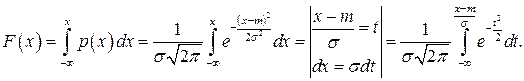
Полученный интеграл нельзя выразить через элементарные функции, но его можно вычислить через специальную функцию

,

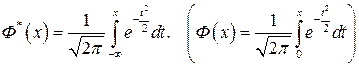называемую нормальной функцией распределения (функцией Лапласа). Значения функции Ф* (х) приводятся в таблице (приложение 2).

Яcно, что 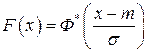. Как и всякая функция распределения, функция Ф*(х) обладает свойствами:

1°. Ф*(х) – неубывающая функция.

2°. Ф*(х) – непрерывная слева.

3°. Ф*(х) – удовлетворяет условиям , .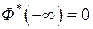

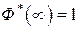Кроме того, Ф*(–х) = 1 – Ф*(х) .

Ее график изображен на рис. 2.18.

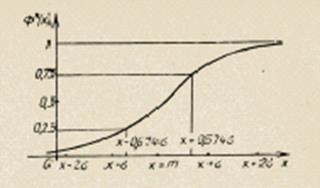
Рис. 2.18

Выясним смысл численных параметров т и , входящих в формулу плотности вероятности (2.18). Для этого найдем основные числовые характеристики нормально распределенной случайной величины Х. Математическое ожидание

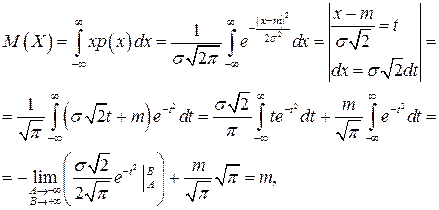
так как первое слагаемое равно нулю, а второй интеграл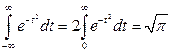

является интегралом Пуассона.

Вычислим дисперсию

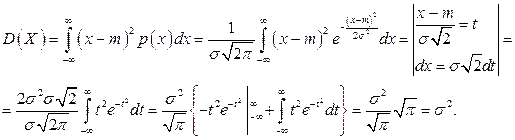
Следовательно, 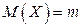, 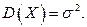Т.е. параметр т является математическим ожиданием, а параметр – средним квадратическим отклонением величины Х.

Так как распределение случайной величины, подчиненной нормальному закону, симметрично относительно х=т, то все центральные моменты нечетного порядка равны нулю. Для центральных моментов четного порядка будем иметь:

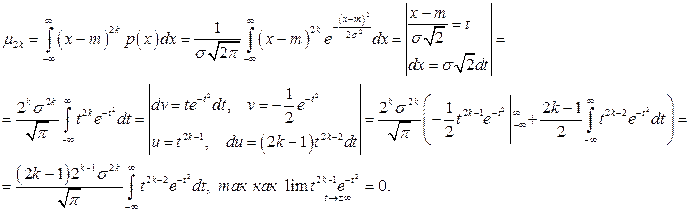
Итак,

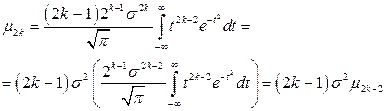(1.19)

откуда следуют соотношения: 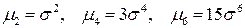и т. д.

Асимметрия 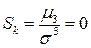, так как для нормального закона .

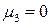Эксцесс 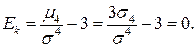Это и естественно, таккак эксцесс характеризует крутость исследуемого закона распределения по сравне­нию с нормальным.

Вероятность попадания случайной величины, подчиненной нормальному закону, в заданный интервал. Пусть случайная величина Х имеет нормальное распределение. Требуется определить вероятность попадания случайной величины Х на интервал (α; β). Для вычисления этой вероятности воспользуемся общей формулой

Р(α<Х<β) =F(β) – F(α),

где F (х) – функция распределения. Но функция распределения F (х) случайной величины Х, подчиняющейся нормальному закону с параметрами т и , имеет вид:

,

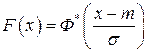где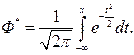

Тогда 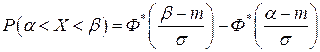(2.20)

или

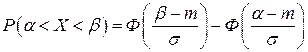, (2.21)

где 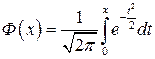– функция Лапласа. Заметим, что Ф(0) = 0 , 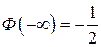, 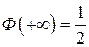и Ф(–х)= –Ф(х) .

Часто на практике требуется вычислить вероятность заданного отклонения Х – М(Х), т. е. вероятность неравенства 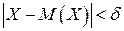. Вероятность отклонения вычисляют с помощью формулы (2.20):

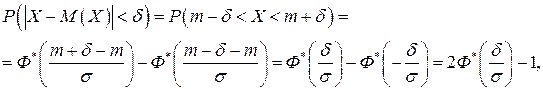
так как Ф*(-х) = 1-Ф*(х) или (2.21), применяя функцию Лапласа,

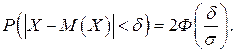(2.22)

Из полученных формул следует, что чем меньше , т. е. чем меньше рассеивание значений случайной величины Х вокруг ее математического ожидания, тем больше увеличивается вероятность принять значение, принадлежащее интервалу (– ; ).

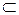Определим далее, какой следует взять интервал с центром в точке х = т, чтобы почти все значения случайной величины принадлежали ему. Для этого будем рассматривать последовательно интервалы: (т– ; т+ ) (т-2 ;т+2 ) 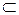( т –3 ;т+3 ) и т.д., и вычислять вероятности того, что значения случайной величины принадлежат этим интервалам:

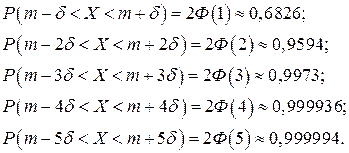
Как видно из вычислений, интервалом практически возможных значений случайной величины будет интервал (т –3 ;т+3 ), так как последующие вероятности увеличиваются незначительно. Это означает, что вероятность того, что абсолютная величина отклонений превысит утроенное среднее квадратическое отклонение, очень мала. Таким образом, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно можно указать интервал ее практически возможных значений. Это правило называется правилом трех сигм.

Пример 2.17. Коробки с шоколадом упаковываются автоматически: средняя масса одной коробки – 1,06 кг. Известно, что только 5 % коробок имеют массу меньше 1 кг. Найти стандартное отклонение, предполагая, что масса коробок распределена нормально.

Решение. Пусть случайная величина Х – масса коробки с шоколадом. Из условия задачи следует, что случайная величина Х распределена нормально и что М(Х) = 1,06. Тогда стандартное отклонение 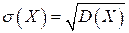найдем, используя равенство:

.

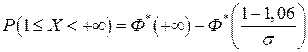Так как только 5 % коробок имеют массу меньше 1 кг и, следовательно, масса остальных коробок больше 1 кг, то можно записать:

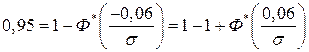или .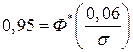

По таблице, прил.2, находим 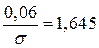, откуда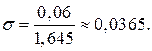

Ответ:среднее квадратическое отклонение массы коробок с шоколадом равно 0,0365 кг.

Пример 2.18. На автоматическом токарном станке изготавливаются болты, номинальная длина которых 30 мм. Наблюдаются случайные отклонения от этого размера, распределенные по нормальному закону с математическим ожиданием т = 0 и средним квадратическим отклонением 1мм. При контроле бракуются все болты, размеры ко­торых отличаются от номинального больше, чем на допуск 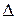= 3,0мм.

Найти вероятность того, что наудачу выбранный болт будет бракованный.

Решение. Рассмотрим случайную величину Х - отклонение размера болта от номинального. Она, согласно условию задачи, распределена по нормальному закону. Тогда вероятность того, что отклонение размера наудачу выбранного болта будет превышать допуск, вычислим по формуле:

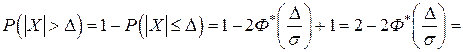
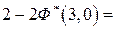
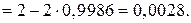
Ответ:вероятность того, что наудачу выбранный болт будет бракованный, равна 0,0028.

Пример 2.19. Случаяйная величина Х подчинена нормальному закону с математическим ожиданием т=0 и средним квадратическим отклонением 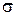. При каком значении 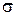вероятность ее попадания в интервал (2; 4) достигает максимума?

Решение. Случаяйная величина Х распределена нормально, поэтому вероятность попадания ее в интервал (2; 4) равна разности значений функции распределения на концах интервала. Применив формулу (2.20)

,

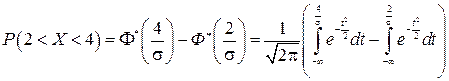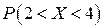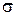замечаем, что вероятность является функцией от . Дифференцируя по вероятность попадания в интервал (2; 4) и приравнивая ее к нулю, получаем:

,

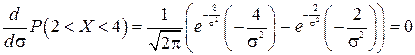откуда 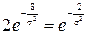и, окончательно, .

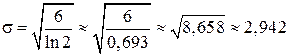Ответ:вероятность попадания случаяйной величины Х в интервал (2; 4) достигает максимума при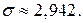

Показательное (экспоненциальное) распределение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается функцией плотности вероятности

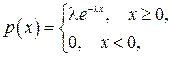
где 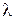>0 постоянна и называется параметром экспоненциального распределе­ния. Примером непрерывной случайной величины, распределенной по показа­тельному закону, может служить время между появлениями двух последова­тельных событий простейшего потока, где 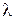- интенсивность потока. Найдем функцию распределения 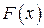случайнойвеличины, распределенной по показательному закону.

Графики плотности вероятности экспоненциального распределения и функции этого распределения изображены соответственно на рис. 2.19 и 2.20.

Рис. 2.19 Рис. 2.20

Определим числовые характеристики случайной величины.

Математическое ожидание

.

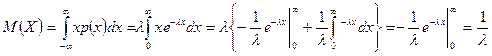Дисперсия

.

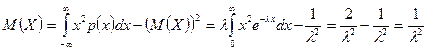Среднее квадратическое отклонение 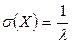и, следовательно, совпадает с математическим ожиданием.

Экспоненциальный закон распределения может применяться в качестве одной из возможных математических моделей в теории надежности. Параметр 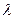в теории надежности называется интенсивностью отказа элемента.

Пример 2.20. При работе ЭВМ в случайные моменты времени возникают неисправности. Время Т работы ЭВМ до первой неисправности распределено по показательному закону .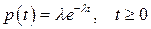

Пусть среднее число неисправностей за сутки работы ЭВМ равно 1,5. При возникновении неисправности тут же устраняются. Предположим, что ремонт продолжается 2,5 ч, после чегоЭВМ снова включается в работу.

Найти вероятность того, что промежуток времени 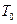между двумя, последовательными неисправностями будет больше 5 ч.

Решение. Случайная величина Т - время между двумя последовательными неисправностями – распределена по показательному закону, плотность вероятностей для которой при условии, что ремонт продолжается 2,5 ч, имеет вид

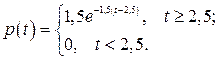
Тогда функцией распределения случайной величины Т будет функция

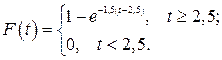
Искомую вероятность того, что промежуток 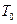между двумя последовательными неисправностями будет больше 5ч при условии, что ремонт длится 2,5 ч, вычислим по формуле

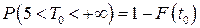, откуда .

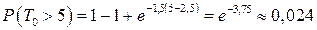Ответ:вероятность того, что промежуток времени 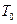между двумя, последовательными неисправностями будет больше 5 ч., равна 0,024.

Вопросы для самопроверки

1. Какой формулой выражается закон равномерной плотности на отрезке?

2. Как вычисляются функция распределения и числовые характеристики равномерно распределенной случайной величины?

3. Какой формулой выражается нормальный закон распределения?

4. Что характеризуют параметры 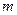и 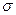нормального закона распределения?

5. Каким свойствам удовлетворяет нормальная функция распределения ?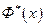

6. По какой формуле вычисляется вероятность попадания случайной величины, подчиненной нормальному закону, на заданный интервал?

7. Что характеризует правило трех сигм?

8. Какой функцией плотности вероятности описывается показательное (экспоненциальное) распределение?

9. С какой числовой характеристикой совпадает среднее квадратическое отклонение показательного закона распределения?

[1] - знак окончания доказательства