Тема: Вычисление частных производных и дифференциалов функций нескольких переменных
Цель: Формирование навыков вычисления частных производных и дифференциалов функций нескольких переменных
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Частная производная (первого порядка) функции нескольких переменных по одному из независимых аргументов определяется как производная этой функции по соответствующему аргументу при условии, что остальные переменные считаются постоянными. При вычислении частных производных используются обычные формулы дифференцирования.
Частной производной функции 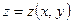 двух независимых переменных
двух независимых переменных 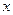 и
и 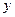 по аргументу
по аргументу 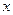 называется производная этой функции по
называется производная этой функции по 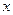 при постоянном
при постоянном 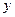 . Аналогично, частной производной функции
. Аналогично, частной производной функции 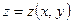 по аргументу
по аргументу 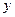 называется производная этой функции, вычисленная при постоянном
называется производная этой функции, вычисленная при постоянном 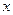 . Частные производные обозначаются следующим образом:
. Частные производные обозначаются следующим образом: 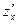 ,
, 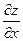 ,
, 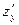 ,
, 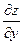 .
.
Полный дифференциал дифференцируемой функции 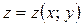 в некоторой точке
в некоторой точке 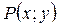 есть выражение вида:
есть выражение вида:
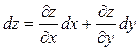 , (18.1)
, (18.1)
где 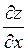 и
и 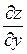 вычисляются в точке
вычисляются в точке 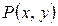 , а дифференциалы независимых переменных равны их приращениям:
, а дифференциалы независимых переменных равны их приращениям: 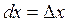 ,
, 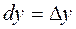 .
.
Формула (18.1) для дифференциала остается в силе, если 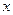 и
и 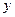 являются функциями каких-либо других аргументов – в этом заключается свойство инвариантности полного дифференциала первого порядка.
являются функциями каких-либо других аргументов – в этом заключается свойство инвариантности полного дифференциала первого порядка.
Аналогично определяется и вычисляется полный дифференциал функции любого числа независимых переменных.
Теоремы и формулы для дифференциалов функций двух, трех и так далее аргументов аналогичны соответствующим теоремам и формулам для функции одного аргумента.
Примеры
Задание 1: Найти частные производные следующих функций:
1) 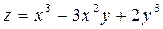 ;
;
2) 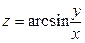 ;
;
3) 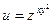 .
.
Решение: 1) При нахождении частной производной по 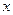 будем рассматривать
будем рассматривать 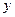 как величину постоянную. Тогда получим
как величину постоянную. Тогда получим
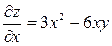 .
.
Аналогично, рассматривая 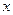 как величину постоянную, найдем частную производную по
как величину постоянную, найдем частную производную по 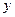 :
:
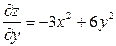 .
.
2) Имеем
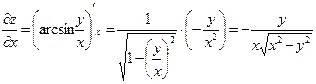 ;
;
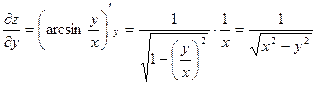 .
.
3) Здесь 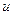 есть функция трех независимых переменных
есть функция трех независимых переменных 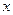 ,
, 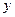 и
и 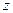 . При вычислении частной производной по каждой из этих переменных две другие следует считать постоянными величинами. Следовательно,
. При вычислении частной производной по каждой из этих переменных две другие следует считать постоянными величинами. Следовательно,
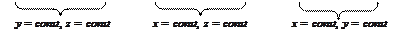
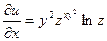 ;
; 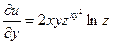 ;
; 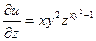
(так как при дифференцировании по 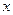 и по
и по 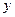 берется производная от показательной функции, а при дифференцировании по
берется производная от показательной функции, а при дифференцировании по 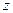 - от степенной функции).
- от степенной функции).
Задание 2: Вычислить полный дифференциал функции 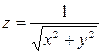 в точке
в точке 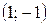 .
.
Решение: Находим частные производные:
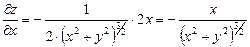 ;
;
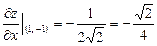 ;
;
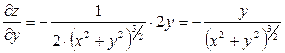 ;
;
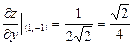 .
.
Таким образом, по формуле (1) получим 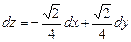 .
.
Задания для практической работы
1. Найдите частные производные следующих функций:
1) 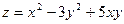 ; 3)
; 3) 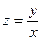 ; 4)
; 4) 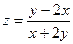 ;
;
5) 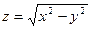 ; 6)
; 6) 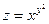 ; 7)
; 7) 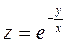 ;
;
8) 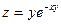 ; 9)
; 9) 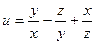 .
.
2. Найдите полные дифференциалы заданных функций:
1) 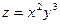 ; 2)
; 2) 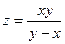 ; 3)
; 3) 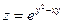 ;
;
4) 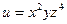 ; 5)
; 5) 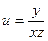 ; 6)
; 6) 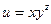 .
.
3. Вычислите значения полных дифференциалов функций:
1) 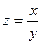 при
при 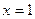 ,
, 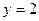 ,
, 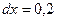 ,
, 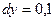 ;
;
3) 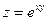 при
при 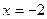 ,
, 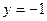 ,
, 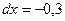 ,
, 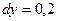 ;
;
4) 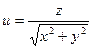 при
при 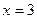 ,
, 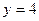 ,
, 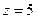 ,
, 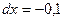 ,
, 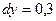 ,
, 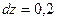 .
.
4. Проверьте, что функция 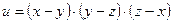 удовлетворяет уравнению
удовлетворяет уравнению 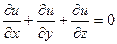 .
.
Контрольные вопросы:
1. Что называется частной производной функции 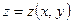 по аргументу
по аргументу 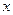 ?
?
2. Что называется частной производной функции 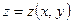 по аргументу
по аргументу 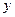 ?
?
3. Дайте определение полного дифференциала функции в некоторой точке.
4. В чем заключается свойство инвариантности полного дифференциала первого порядка?
Рекомендуемая литература: 1.2[с. 438-439],2.2[с. 151-166] 2.2[с. 151-166].
СПИСОК ЛИТЕРАТУРЫ
1. Основная:
1.1 Богомолов, Н.В. Математика [Текст]: учебник для бакалавров / Н.В. Богомолов, П.И.Самойленко. - 5-е изд. - М.: Юрайт, 2014. - 396 с.
1.2 Богомолов, Н.В. Практические занятия по математике [Текст]: учебное пособие для бакалавров / Н.В. Богомолов. - 11-е изд. - М.: Юрайт, 2015. - 495 с.
1.3 Шипачев, В.С. Основы высшей математики: учебник и практикум/ В.С.Шипачев.-8-е изд. - М.: Юрайт, 2014. - 447 с.
2.Дополнительная:
2.1 Данко, П.Е., Высшая математика в упражнениях и задачах. В 2 ч. Ч.1: учеб. пособие для вузов / П.Е.Данко, А.Г. Попов, Т.Я. Кожевникова. – 8-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2014. – 304 с.
2.2 Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2: Учеб. пособие для вузов / П.Е.Данко, А.Г. Попов, Т.Я. Кожевникова. – 8-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование»», 2014. – 416 с.
Учебное издание
ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Методические указания по выполнению практических работ
Составитель
