Тема: Вычисление производных функций по определению производной

Цель: Формирование навыков вычисления производных функций по определению производной

Время выполнения: 2 часа.

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Производной функции 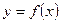в точке 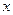(производной первого порядка) называется предел отношения приращения функции к приращению аргумента , когда последнее стремится к нулю:

(10.1)

Если этот предел конечен, то функция 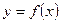называется дифференцируемой в точке 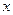; в противном случае (то есть если он не существует или равен бесконечности) – не дифференцируемой. В том случае, когда предел есть бесконечность, говорят, что функция 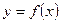имеет в точке бесконечную производную.

Дифференциалом функции 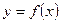(дифференциалом первого порядка) называется главная часть ее приращения, пропорциональная приращению независимой переменной .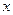

Дифференциал независимой переменной 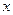равен ее приращению :

. (10.2)

Дифференциал любой дифференцируемой функции 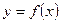равен произведению ее производной на дифференциал независимой переменной:

. (10.3)

Соотношение (10.3) остается в силе и тогда, когда 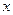есть функция другого аргумента – в этом заключается инвариантность формы первого дифференциала.

Из соотношения (10.3) получаем , то есть производная первого порядка функции 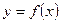равна отношению первого дифференциала функции к дифференциалу ее аргумента.

Пример

Задание: Пользуясь определением производной, найти производную и дифференциал функции . Вычислить .

Решение: Найдем приращение функции , соответствующее данному приращению аргумента :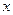

.

Тогда и

.

По формуле (10.1) находим дифференциал функции:

.

Подставляя в выражение для значение , получим

.

Задания для практической работы

1. Найдите производные и дифференциалы от указанных функций, пользуясь непосредственно определением производной:

1) ; 2) ; 3) ;

4) ; 5) ; 6) .

2. Дана функция . Найдите .

3. Дана функция . Найдите .

4. Дана функция . Найдите , .

5. Дана функция . Найдите , .

6. Дана функция . Покажите, что .

Контрольные вопросы:

1. Дайте определение производной первого порядка.

2. Какая функция называется дифференцируемой? Какая функция называется не дифференцируемой?

3. Что называется дифференциалом первого порядка?

4. Сформулируйте определение дифференциала функции.

5. В чем заключается инвариантность формы первого дифференциала.

6. Сформулируйте общее правило нахождения производной функции.

Рекомендуемая литература: 1.1[с. 211-236], 1.2[с.180-184],1.3[с.242-243].

Практическая работа №11

Тема: Вычисление производных сложных функций

Цель: Формирование навыков вычисления производных сложных функций

Время выполнения: 2 часа

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Пусть и - дифференцируемые функции. Тогда сложная функция есть также дифференцируемая функция, причем

, или (11.1)

Это правило распространяется на цепочку из любого количества дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.

Пример

Задание: Найдите производные функций:1) ; 2) .

Решение: 1) Предположим, что , где . Тогда по формуле (1) найдем

.

2) Предполагая, что , , , получим

.

Задания для практической работы

Вычислите производные заданных функций, пользуясь основы формулами и правилами:

1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) ; 8) ;

9) ; 10) .

Контрольные вопросы:

1. Дайте определение производной функции.

2. Перечислите правила нахождения производной функции.

3. Какие функции называются дифференцируемыми?

4. Какая функция называется сложной?

5. Как найти производную сложной функции?

Рекомендуемая литература: 1.1[с. 250-254], 1.2[с.180-184], 1.3[с.266-270].

Практическая работа №12