Лабораторная работа № 1. СТАНДАРТНЫЙ МОДУЛЬ СRT

В 2 частях

ЧАСТЬ 2

Минск

БНТУ

УДК 004(076.5)

ББК 32.81 я 7

И 74

Составители:

Л.А.Тарасевич, Е.В. Пронкевич

Рецензенты:

В.А. Булат, В.Б. Козловская

В лабораторном практикуме рассматриваются основы программирования на языке TURBO PASCAL 7.0 с использованием стандартного модуля CRT, основные приемы численных методов, относящиеся к решению нелинейных уравнений, систем нелинейных и линейных алгебраических уравнений, интегрированию функций, решению задач аппроксимации функций, обыкновенных дифференциальных уравнений. Значительное внимание уделяется вопросам алгоритмизации методов.

Лабораторный практикум рассчитан для студентов специальностей 1- 43 01 04 «Тепловые электрические станции» дневной и заочной формы обучения, 1-53 01 04 «Автоматизация и управление энергетическими процессами» дневной формы обучения, 1-43 01 08 «Паротурбинные установки атомных электрических станций» дневной формы обучения.

Часть 1 (авторы Л.А. Тарасевич, Е.В. Пронкевич, Ю.Б. Попова) издана в БНТУ в 2007 г.

Ó Белорусский национальный технический университет, 2011

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 5

Лабораторная работа № 1. СТАНДАРТНЫЙ МОДУЛЬ СRT. 6

1.1. Программирование клавиатуры.. 6

1.2. Текстовый вывод на экран. 9

1.3. Программирование звукового генератора. 16

1.4. Меню.. 19

Лабораторная работа № 2. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.. 22

2.1. Метод бисекции. 22

2.2. Метод хорд. 24

2.3. Метод простой итерации. 26

2.4. Метод Ньютона (метод касательных) 31

2.5. Задание. 36

2.6. Контрольные вопросы.. 37

Лабораторная работа № 3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.. 38

3.1. Методы исключения неизвестных (Метод Гаусса) 39

3.2. Задание. 42

3.3. Контрольные вопросы.. 43

3.4. Итерационные методы.. 44

3.5. Задание. 47

3.6. Контрольные вопросы.. 48

Лабораторная работа № 4. ИНТЕРПОЛИРОВАНИЕ. 49

4.1. Метод Лагранжа. 51

4.2. Линейная интерполяция. 54

4.3. Задание. 56

4.4. Контрольные вопросы.. 59

Лабораторная работа № 5. РЕШЕНИЕ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 60

5.1. Метод Ньютона. 60

5.2. Задание. 62

5.3. Контрольные вопросы.. 63

Лабораторная работ № 6. РЕШЕНИЕ ЗАДАЧИ АППРОКСИМАЦИИ.. 64

6.1. Метод наименьших квадратов (полином второй степени) 64

Блок-схема. 67

6.2. Задание. 68

6.3. Контрольные вопросы.. 70

Лабораторная работа № 7. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 71

7.1. Метод прямоугольников. 73

7.2. Метод трапеций. 76

7.3. Метод Симпсона. 78

7.4. Задание. 81

7.5. Контрольные вопросы.. 83

Лабораторная работа № 8. РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА.. 84

8.1. Метод Эйлера (метод Рунге – Кутта 1-го порядка) 85

8.2. Модифицированный метод Эйлера (метод Рунге – Кутта 2-го порядка) 91

8.3. Метод усредненных точек. 94

8.4. Метод Рунге – Кутта четвертого порядка. 97

8.5. Задание. 101

8.6. Контрольные вопросы.. 102

ЛИТЕРАТУРА.. 114

ВВЕДЕНИЕ

В данном практикуме приведены основы программирования на языке TURBO PASCAL 7.0 с использованием модуля CRT, основы численных методов решения нелинейных уравнений, систем линейных алгебраических уравнений, систем нелинейных алгебраических уравнений, вычисления определенных интегралов, обыкновенных дифференциальных уравнений 1-го и 2-го порядка. Дополнительно рассматриваются интерполирование, аппроксимация.

Практикум может быть использован при выполнении лабораторных, курсовых работ. Каждая лабораторная работа содержит теоретическое обоснование, блок-схемы рассматриваемых методов и упражнения для самостоятельной работы и завершается контрольными вопросами по данной теме.

Лабораторная работа № 1. СТАНДАРТНЫЙ МОДУЛЬ СRT

В стандартном модуле CRT сосредоточены процедуры и функции, обеспечивающие управление текстовым режимом работы экрана. С помощью входящих в модуль подпрограмм можно перемещать курсор в произвольную позицию экрана, менять цвет выводимых символов и окружающего их фона, создавать окна.

Кроме того, в модуль включены процедуры Sound, NoSound, Delay, которые позволяют программировать звуковой генератор ПК.

Программирование клавиатуры

Дополнительные возможности управления реализуются двумя функ-циями: KeyPressed и ReadKey.

Функция KeyPressed возвращает значение типа Boolean, указывающее состояние буфера клавиатуры: False означает, что буфер пуст, а True – что в буфере есть хотя бы один символ, еще не прочитанный программой.

В MS – DOS реализуется так называемый асинхронный буферизован- ный ввод с клавиатуры. По мере нажатия на клавиши соответствующие коды помещаются в особый буфер, откуда они могут быть затем прочитаны про- граммой. Стандартная длина буфера рассчитана на хранение до 16 кодов символов. Если программа достаточно долго не обращается к клавиатуре, а пользователь нажимает клавиши, буфер может оказаться переполненным. В этот момент раздается звуковой сигнал и «лишние» коды теряются. Чтение из буфера обеспечивается процедурами Read / Readln и функцией ReadKey. Об-ращение к функции KeyPressed не задерживает исполнение программы: функция немедленно анализирует буфер и возвращает то или иное значение, не дожидаясь нажатия клавиши.

Функция ReadKey возвращает значение типа Char. При обращении к этой функции анализируется буфер клавиатуры: если в нем есть хотя бы один непрочитанный символ, код этого символа берется из буфера и возвращается в качестве значения функции, в противном случае функция будет ожидать нажатия на любую клавишу.

Пусть, например, в какой – то точке программы необходимо игнориро-

вать все ранее нажатые клавиши, коды которых еще не прочитаны из буфера, т. е. необходимо очистить буфер.

Этого можно достичь следующим образом:

Uses CRT;

Var C: Char;

Begin

While KeyPressed do

C := ReadKey;

. . .

end.

При использовании процедуры ReadKey необходимо учесть, что в кла- виатурный буфер помещаются так называемые расширенные коды нажатых клавиш. Если нажимается любая алфавитно-цифровая клавиша, расширенный код совпадает с ASCII кодом соответствующего символа. Например, если нажимается клавиша с латинской буквой «а» (в нижнем регистре), функция ReadKey возвращает значение chr(97), а если «А» (в верхнем регистре) – значение chr(65). При нажатии функциональных клавиш F1…F10, клавиш управления курсором, клавиш Ins, Home, Del, End, PgUp, PgDn в буфер помещается двухбайтная последовательность: сначала символ # 0, а затем расширенный код клавиши. Таким образом, значение # 0, возвращаемое функцией ReadKey, используется исключительно для того, чтобы указать программе на генерацию расширенного кода. Получив это значение, про- грамма должна еще раз обратиться к функции, чтобы прочитать расширенный код клавиши, т. е. код сканирования клавиши. (Этот код определяется порядком, в соответствии с которым микропроцессор клавиатуры Intel 8042 периодически опрашивает (сканирует) состояние клавиш).

Следующая программа позволяет определить расширенный код любой

клавиши:

Uses CRT;

Var

C: Char;

Begin

repeat

C:= ReadKey;

If C<># 0 then

Writeln (ord (C))

else

Wtiteln (′0′, ord (ReadKey):8)

until C = # 27 {27 – расширенный код клавиши Esc}

end.

Для завершения работы программы нужно нажать клавишу Esc.

Если воспользоваться этой программой, то обнаружится, что нажатие на некоторые клавиши игнорируется функцией ReadKey. Это, прежде всего, так называемые сдвиговые клавиши – Shift, Ctrl, Alt. Сдвиговые клавиши в MS – DOS обычно используются для переключения регистров клавиатуры и нажимаются в сочетании с другими клавишами. Именно таким способом, например, различается ввод прописных и строчных букв.

Текстовый вывод на экран

Используемое в ПК устройство визуального отображения информации – дисплей – состоит из двух основных частей: монитора, содержащего экран с необходимыми компонентами (устройствами развертки изображения), и блока управления, который чаще называют адаптером. Обычно оба устройства согласуются друг с другом, но в отдельных случаях этого согласования может не быть (например, цветной монитор может работать с монохромным адаптером и наоборот). Здесь будем считать оба устройства согласованными, поэтому, говоря о различных дисплеях, будем говорить только о различных адаптерах, так как именно в них сосредоточены основные отличия дисплеев друг от друга.

1. Процедура TextMode используется для задания одного из возможных текстовых режимов работы адаптера. Заголовок процедуры:

Procedure TextMode (Mode: Word);

Здесь Mode – код текстового режима. В качестве значения этого выраже-ния могут использоваться следующие константы, определенные в модуле CRT:

const

BW40=0; {Черно-белый режим 40x25}

Co40=1; {Цветной режим 40x25}

BW80=2; {Черно-белый режим 80x25}

Co80=3; {Цветной режим 80x25}

Mono=7; {Используется с MDA}

Font8x8=256; {Используется для загружаемого шрифта в

режиме 80x43 или 80x50 с адаптерами EGA

или VGA}

Код режима, установленного с помощью процедуры TextMode, запо-минается в глобальной переменной LastMode модуля CRT и может использоваться для восстановления начального состояния экрана.

Следующая программа иллюстрирует использование этой процедуры в различных режимах. Отметим, что при вызове TextMode сбрасываются все ранее сделанные установки цвета и окон, экран очищается и курсор перево- дится в его левый верхний угол.

Uses CRT;

Procedure Print (S: String);

{Выводит сообщение S и ждет инициативы пользователя}

begin

WriteLn (S); {Выводим сообщение}

WriteLn (′Нажмите клавишу Enter…′);

ReadLn {Ждем нажатия клавиши Enter}

end; {Print}

var

LM: Word; {Начальный режим экрана}

begin

LM := LastMode; {Запоминаем начальный режим работы дисплея}

TextMode (Co40);

Print (′Режим 40x25′);

TextMode (Co80);

Print (′Режим 80x25′);

TextMode (Co40+Font8x8);

Print (′Режим Co40+Font8x8′);

TextMode (Co80+Font8x8);

Print(′Режим Co80+Font8x8′); {Восстанавливаем исходный режим работы}

TextMode (LM);

end.

2. Процедура TextColor определяет цвет выводимых символов. Заголовок процедуры:

Procedure TextColor (Color:Byte);

3. Процедура TextBackGround определяет цвет фона. Заголовок:

Procedure TextBackGround (Color:Byte);

Параметр Color определяет цвет выводимого символа, представляет

собой выражение целого типа (см. табл. 1.1).

Таблица. 1.1

Константы, соответствующие различным цветам

Цвет символов	Цвет фона	Название	Обозначение
Черный Синий Зеленый Бирюзовый Красный Сиреневый Коричневый Белый Серый Голубой Светло-зеленый Светло-бирюзовый Светло-красный Светло-сиреневый Желтый Ярко-белый Мерцание символа	Черный Синий Зеленый Бирюзовый Красный Сиреневый Коричневый Светло-серый	Black Blue Green Cyan Red Magenta Brown LightGray Gray LightBlue LightGreen LightCyan LightRed LightMagenta Yellow White Blink

Параметр Color – выражение целого типа, обозначающее устанавли-

ваемый цвет фона, на котором выводятся символы.

4. Процедура ClrScr очищает экран или окно. После обращения к ней экран (окно) заполняется цветом фона и курсор устанавливается в его левый верхний угол. Например:

Uses CRT;

var

C: Char;

begin

TextBackGround (red); {Заполняем экран красным цветом}

ClrScr;

WriteLn (′Нажмите любую клавишу…′);

C:= ReadKey; {Ждем нажатия любой клавиши}

TextBackGround (Black);

ClrScr {Восстанавливаем черный фон экрана}

end.

5. Процедура Window определяет текстовое окно – область экрана, которая в дальнейшем будет рассматриваться процедурами вывода как весь экран. Сразу после вызова процедуры курсор помещается в левый верхний угол окна, а само окно очищается (заполняется цветом фона). По мере вывода курсор, как обычно, смещается вправо и при достижении правой границы окна переходит на новую строку, а если он к этому моменту находился на последней строке, содержимое окна сдвигается вверх на одну строку, то есть осуществляется «прокрутка» окна. Заголовок процедуры:

Procedure Window (X1, Y1, X2, Y2: Byte);

Здесь X1, Y1 – координаты левого верхнего угла окна, X2, Y2 – правого нижнего угла окна. Они задаются в координатах экрана, причем левый верхний угол экрана имеет координаты (1, 1), горизонтальная координата увеличивается слева направо, а вертикальная сверху вниз.

6. Процедура GotoXY переводит курсор в нужное место экрана или текущего окна. Заголовок процедуры:

Procedure GotoXY (X, Y:Byte);

Здесь X, Y – новые координаты курсора. X – столбец, Y – строка. Коор- динаты задаются относительно границ экрана (окна), т. е. оператор

GotoXY (1, 1);

означает перевести курсор в левый верхний угол экрана (или окна, если к тому моменту на экране определено окно). Обращение к процедуре игнорируется, если новые координаты выходят за границы экрана (окна).

Рассмотрим процедуру черчения рамок.

Procedure Frame (X1, Y1, X2, Y2:integer);

{X1, Y1, X2, Y2 – координаты соответственно левого верхнего и правого нижнего угла рамки}

const

{для черчения двойной линии}

a=#186; b=#187; c=#188;

d=#200; e=#201; f=#205;

{для черчения одинарной линии}

a=#179; b=#191; c=#217;

d=#192; e=#218; f=#198;

var i,j:integer;

begin

GotoXY(X1,Y1);

write(e);

for i:=(X1+1) to (X2-1) do write(f);

write(b);

for i:=(Y1+1) to (Y2-1) do

begin

gotoXY(X1,i);

write(a);

gotoxy(X2,i);

write(a);

end;

gotoxy(X1,Y2);

write(d);

for i:=(X1+1) to (X2-1) do

write(f);

write(c);

end.

Рассмотрим процедуру выделения ограниченного рамкой окна с заданным фоном.

Procedure FrameFon(V1,V2,V3,V4,Fon:Byte);

Begin

Frame (V1,V2,V3,V4);

Window(V1+1, V2+1, V3-1, V4-1);

TextBackGround(Fon);

ClrScr;

End.

7. Функции WhereX и WhereY. С помощью этих функций типа Byte можно определить текущие координаты курсора: WhereX возвращает его го- ризонтальную, а WhereY – вертикальную координаты.

Три следующие процедуры без параметров могут оказаться полезными при разработке текстовых редакторов.

8. Процедура ClrEOL стирает часть строки от текущего положения курсора до правой границы окна (экрана). Положение курсора не меняется.

9. Процедура DelLine уничтожает всю строку с курсором в текущем окне (или на экране, если окно не создано). При этом все строки ниже уда- ляемой (если они есть) сдвигаются вверх на одну строку.

10. Процедура InsLine вставляет строку: строка с курсором и все строки ниже ее сдвигаются вниз на одну строку. Строка, вышедшая за нижнюю границу окна (экрана), безвозвратно теряется. Текущее положение курсора не меняется.

11. Процедуры LowVideo, NormVideo и HighVideo. С помощью этих процедур без параметров можно устанавливать соответственно пониженную, нормальную и повышенную яркость символов. Например:

Uses CRT;

begin

LowVideo;

WriteLn (′Пониженная яркость′);

NormVideo;

WriteLn (′Нормальная яркость′);

HighVideo;

WriteLn (′Повышенная яркость′);

end.

На практике нет разницы между пониженной и нормальной яркостью

изображения.

12. Процедура AssignCRT. Связывает текстовую файловую переменную F c экраном с помощью непосредственного обращения к видеопамяти (т. е. к памяти, используемой адаптером для создания изображения на экране). В результате вывод в такой текстовый файл осуществляется значительно (в 3…5 раз) быстрее, чем если бы этот файл был связан с экраном стандартной процедурой Assign. Заголовок процедуры:

Procedure AssignCRT (F: Text);

Метод бисекции

Алгоритм решения нелинейного уравнения:

1. ;

2. ;

3. Если , то .

Если , то .

4. Критерий окончания счета:

Метод хорд

Алгоритм решения нелинейного уравнения:

1. Если , то на отрезке существует корень.
2. Если , то и ,

Если , то и ,

3. Критерий окончания счета:

Метод простой итерации

Постановка задачи:

Дано нелинейное уравнение

. (2.2)

Корень отделен x^* Î [a; b]. Требуется уточнить корень с точностью ε.

Уравнение (2.2) преобразуем к эквивалентному виду

x = φ(x). (2.3)

Выберем начальное приближение x₀Î [a; b].

Вычислим последовательно новые приближения корня:

x₁=φ(x₀);

x₂=φ(x₁); (2.4)

………..

x_i=φ(x_i-1) ,

i = 1, 2, … где i – номер итерации.

Последовательное вычисление значений x_i по формуле (2.4) называется итерационным процессом метода простых итераций, а сама формула – формулой итерационного процесса метода.

Если , то итерационный процесс сходящийся.

Условие сходимости

(2.5)

Точное решение x^* получить невозможно, так как требуется бесконечныйитерационный процесс.

Итерационный процесс заканчивается при выполнении условия

, (2.6)

где ε – заданная точность; i – номер последней итерации.

Условие завершения итерационного процесса (2.6) обеспечивает близость значения x_i к точному решению:

Рассмотрим геометрическую иллюстрацию метода простых итераций.

Уравнение (2.3) представим на графике в виде двух функций: y₁ = x и y₂ = φ(x).

Возможные случаи взаимного расположения графиков функций и, соответственно, видов итерационного процесса показаны на рис. 1.1 – 1.4.

Рис. 1.1. Итерационный процесс для случая 0< <1 xÎ[a, b].

Рис. 1.2. Итерационный процесс для случая –1< <1 xÎ[a, b].

Рис. 1.3. Итерационный процесс для случая >1 xÎ[a, b].

Рис. 1.4. Итерационный процесс для случая £ – 1 xÎ[a, b].

Из анализа графиков следует, что скорость сходимости растет при уменьшении значения

Алгоритм нахождения корня методом простых итераций:

1. Если , то .

Если , то .

2. Уравнение преобразуем к виду:

или

,

где ,

3. Условие сходимости метода простой итерации:

.

4. Критерий окончания счета:

.

Простой итерации

Задание

Решить нелинейные уравнения методами:

1) бисекции;

2) хорд;

3) простой итерации;

4) Ньютона.

Варианты заданий:

№ варианта	Уравнение	Интервал изоляции корня
		[1,57; 3,14]
		[0; 1]
		[0,4; 1]
		[0,5; 1]
		[2; 3]
		[1; 2]
		[19,5; 21,2]
		[2; 3]
		[0,8; 1,0]
		[-2; 1]
		[0,618; 0,667]
		[0,4; 0,5]
		[0; 1]
		[2,2; 2,4]
		[2; 3]
		[0; 1]

2.6. Контрольные вопросы

1. В чем сущность методов бисекции, хорд, простой итерации, Ньютона?

2. Как выбирается начальное приближение в методах простой итерации и Ньютона?

3. К какому виду нужно преобразовать уравнение для метода простой итерации?

Задание

Решить системы ЛАУ методом Гаусса.

Варианты заданий:

№ варианта	Система уравнений

3.3. Контрольные вопросы

1. К какому виду приводится матрица в методе Гаусса?

2. В каком случае нельзя применить метод Гаусса?

3. Что нужно предусмотреть при использовании метода Гаусса?

Итерационные методы

Метод называется приближенным, если при точном выполнении всех требуемых действий и при точных коэффициентах мы получаем, как правило, лишь приближенный результат.

Впрочем, практически и при применении точного метода результат оказывается приближенным по двум причинам: во-первых, коэффициенты уравнений обычно бывают приближенными числами; во-вторых, промежуточные вычисления на практике обычно невозможно выполнять с полной точностью. Значит, погрешность окончательного результата складывается из неустранимой погрешности задания исходных данных (коэффициентов) и погрешностей округления.

В случае применения приближенного метода на окончательный результат влияет всегда погрешность метода, также на практике обычно имеет место неустранимая погрешность в задании коэффициентов и погрешность округления в промежуточных действиях.

Одношаговый линейный стационарный итерационный процесс называется методом простой итерации (МПИ).

Пусть дана система ЛАУ с неособенной матрицей. В методе простой итерации ее предварительно приводят к виду:

.

Для очень больших систем, когда метод Гаусса становится неэффективным, применяют итерационные методы, например, метод простой итерации или метод Зейделя.

Метод простой итерации

Вычисления по методу простой итерации начинаются с произвольного вектора X⁰ ={x₁⁰, x₂⁰ , ... , x_n⁰}. Итерационный процесс осуществляется по формуле:

т. е. все неизвестные на следующей итерации вычисляются только через неизвестные на предыдущей итерации.

Условия завершения итерационного процесса:

d £ e (1)

где e – требуемая точность;

d – оценка достигнутой точности.

(2)

или

. (3)

Условие сходимости итерационного процесса (условие преобладания диагональных коэффициентов):

, (4)

Метод Зейделя

Метод Зейделя отличается от простой итерации тем, что найдя какое-то приближение для компоненты, мы сразу же используем его для отыскания следующей компоненты.

В методе Зейделя используется итерационная формула

,

в которой при вычислении очередного неизвестного используются последние найденные значения остальных неизвестных. Вычисления заканчиваются, когда невязки системы становятся достаточно малыми. Итерационные методы сходятся не для всякой матрицы. Достаточным условием сходимости является положительная определенность матриц.

Задание

Решить системы линейных алгебраических уравнений методами:

1) простой итерации;

2) метод Зейделя.

Варианты заданий:

№ варианта	Система уравнений	Точность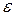

Контрольные вопросы

1. Чем отличаются точные методы от итерационных?

2. Как выбираются начальные приближения в методах простой итерации и Зейделя?

3. Каково условие прекращения итерации в методе простой итерации и в методе Зейделя для решения систем линейных алгебраических уравнений?

Метод Лагранжа

Пусть - набор различных точек (узлов) на отрезке , в котором заданы значения достаточно гладкой функции так, что , . Требуется построить многочлен степени не выше , принимающий в точках значения , и оценить погрешность приближения функции этим многочленом на всем отрезке .

Введем в явном виде вспомогательные многочлены степени , удовлетворяющие условиям по формулам:

. (4.1)

Тогда интерполяционный многочлен можно задать по формуле Лагранжа:

, (4.2)

при этом удобно преобразовать к виду:

, (4.3)

где .

Разность называется погрешностью интерполирования, или остаточным членом интерполирования. В узлах интерполирования погрешность обращается в нуль, в остальных точках она отлична от нуля, но если – многочлен степени , то . Если функция имеет непрерывную - ю производную, то остаточный член можно представить в виде

, (4.4)

где – некоторая точка, лежащая на отрезке, содержащем узлы и точку .

Пример 1. Построить многочлен наименьшей степени, принимающий в данных точках следующие значения:

х	– 1
y	– 14	– 5

По формуле (4.1) вычислим вспомогательные многочлены:

,

,

,

.

Затем по формуле (4.2) построим интерполяционный многочлен Лагранжа:

.

Линейная интерполяция

Линейная интерполяция состоит в том, что заданные точки 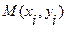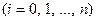соединяются прямолинейными отрезками и функция 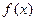приближается к ломаной с вершинами в данных точках. Поскольку имеется n интервалов 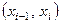, то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности для i-го интервала можно записать уравнение прямой, проходящей через точк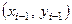и и 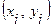, в виде:

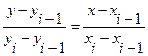
Отсюда

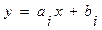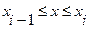, , (4.5)

, .

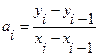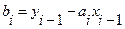Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (4.5) и найти приближенное значение функции в этой точке.

Варианты заданий

№ вар.	Условие	f(x)
	x		96,2		104,2	108,7		f(102)
f(x)	11,38	12,8	14,7	17,07	19,91
	x							f(5)
f(x)
	x		2,3	2,5	3,0	3,5	3,8		f(3,75)
f(x)	5,848	6,127	6,3	6,694	7,047	7,243	7,368
	x						f(20)
f(x)	68,7			39,1
						&n