Определение уравновешивающей силы методом Жуковского
Основная теорема Жуковского. В некоторых технических задачах требуется определить только уравновешивающий момент 
или уравновешивающую силу 
. В таких случаях применяют теорему Н.Е. Жуковского о жестком рычаге, суть которой заключается в следующем: «Если в соответствующих точках повернутого на 90° плана скоростей приложить все внешние силы, действующие на звенья механизма, включая силы инерции, и рассматривать повернутый план как жесткий рычаг с опорой в полюсе 
, то он будет находиться в равновесии».
Следовательно, если задан механизм и все внешние силы, приложенные к нему, то для нахождения уравновешивающей силы можно поступить следующим образом:
a) Построить план скоростей механизма и повернуть его на 90°;
b) Найти на этом плане скоростей по правилу подобия точки приложения заданных и определенных внешних сил;
c) Параллельно самим себе перенести из схемы механизма в одноименные точки плана скоростей силы, включая уравновешивающую силу;
d) Принять повернутый план скоростей за рычаг с опорой в полюсе , написать уравнение равновесия системы и из него найти величину уравновешивающей силы .
Необходимо учесть, что если к какому-либо звену приложен момент, то его следует представить в виде пары сил, которые переносятся в соответствующие точки повернутого плана скоростей. Составляющие пары сил можно определит по формуле:
, (3.9)
где 
– расстояние между точками А и В приложения сил 
и 
, образующих пару с моментом М.
Пример №8. По данным примеров №3, №5 и №7 для кривошипно-ползунного механизма (рис. 3.9а) найти величину уравновешивающей силы , приложенной в точке А перпендикулярно кривошипу 1 методом рычага Жуковского и сравнить полученный результат с величиной уравновешивающей силы, рассчитанной при помощи кинетостатического анализа в примере №7.
Дано: 
, 
, 
, 
, 
, 
, 
.
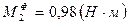Решение:
Рис. 3.9. Схема к определению уравновешивающей силы кривошипно-ползунного механизма: а) схема механизма: б) план скоростей; в) план скоростей, повернутый на 90°, с приложенными силами
Построить план скоростей, повернутый на 90°, можно путем поворота обычного плана скоростей на угол 90°. На повернутый план скоростей со схемы механизма (рис. 3.9а) переносим параллельно самим себе внешние силы в одноименные точки: 
и 
в точку 
; 
, 
и 
в точку 
; уравновешивающую силу прикладываем в точке 
.
Момент инерции 
представим в виде пары сил 
и 
, приложенных в точках и , перпендикулярно 
так, чтобы их направление совпадало с направлением вращения на схеме механизма (а именно – против хода часовой стрелки).Модуль этих сил определим по формуле (3.9):
.
На плане скоростей, повернутом на 90°, находим плечи сил относительно полюса . Для удобства рассмотрим его отдельно и введем буквенное обозначение (см. рис. 3.10).
Рис. 3.10. Схема к определению уравновешивающей силы
Составляем уравнение моментов сил относительно полюса :
,
отсюда находим величину уравновешивающей силы :
,
Расхождение результатов составляет:
.
Расхождение результатов объясняется погрешностью построений и измерений при кинетостатическом анализе механизма.