Определение класса плоских механизмов

Механизмы подразделяются на классы. В основу классификации положен принцип структурного образования механизмов, сформулированный в 1914 году русскими учеными Л.В. Ассуром и И.И. Артоболевским. Согласно этому принципу, схема любого механизма может быть составлена последовательным присоединением к ведущему звену (или ведущим звеньям) и стойке кинематических цепей с числом степеней свободы равным нулю, т.е. W= 0. Такие кинематические цепи называют структурными группами или группами Ассура.

Группа Ассура – это кинематическая цепь с нулевой степенью свободы относительно тех звеньев, с которыми входят в кинематические пары свободные элементы ее звеньев и не распадающиеся на более простые цепи с нулевой степенью свободы.

Согласно структурной формуле Чебышева, для плоской кинематической цепи число степеней свободы механизма W можно вычислить следующим образом:

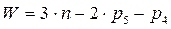, (1.1)

где n – число подвижных звеньев;

р₅– число пар V класса;

р₄– число пар IV класса.

Рассмотрим принцип построения механизмов методом наслоения групп Ассура на примере плоского механизма с одной степенью свободы, у которого положение всех звеньев определяется заданием одной обобщенной координаты. Построение механизма начинается с объединения ведущего звена и стойки. Согласно классификации Ассура-Артоболевского, полученный таким образом механизм называется начальным механизмом 1-го класса. Начальный механизм имеет одну степень свободы. Более сложные механизмы образуются присоединением к начальному механизму групп Ассура. В данном курсе такие группы Ассура будут все 2-го класса.

Если механизм имеет в своем составе только группы Ассура 2-го класса, то его следует отнести к механизмам 2-го класса.

Пример №1. Выполнить структурный анализ механизма, представленного на рис.1.5.

Рис. 1.5.Иллюстрация к примеру №1

Для проведения структурного анализа механизма, необходимо выполнить следующие действия:

1) пронумеровать звенья, определить их количество, дать им название, определить количество кинематических пар IV и V классов;

2) охарактеризовать заданную кинематическую цепь;

3) определить число степеней свободы механизма по формуле Чебышева;

4) выделить группы Ассура1-го и 2-го классов, определить их количество;

5) определить класс механизма.

Решение:

1) Механизм состоит из пяти звеньев: 0 – стойка, 1 – кривошип, 2 – ползун, 3 – кулиса, 4 – шатун, 5 – ползун.

Звено 1 является ведущим звеном. Механизм преобразует вращательное движение кривошипа 1 в поступательное движение ползуна 5.Звенья соединяются друг с другом при помощи семи кинематических пар: 0-1, 1-2, 2-3, 3-0, 3-4, 4-5, 5-0. Все кинематические пары V класса. Кинематических пар IV класса нет.

2) Заданная кинематическая цепь является сложной, замкнутой, плоской.

3) Число степеней свободы определяем по формуле Чебышева (1.1):

,

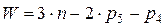в которой 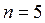, , 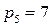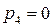. Тогда

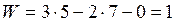
Таким образом, механизм обладает одной степенью свободы.

4) Выделим группы Ассура, определим их количество и класс.

4.1) Кривошип 1 является ведущим звеном и в соединении со стойкой 0 образует группу Ассура1-го класса (рис. 1.6а).

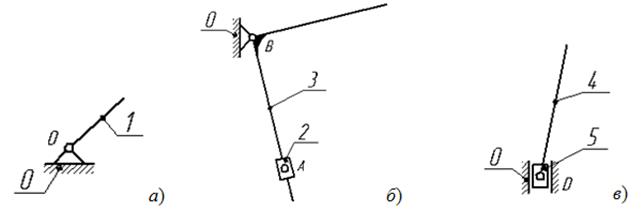
Рис. 1.6.

4.2) Кулиса 3 и ползун 2 образуют группу Ассура2-го класса с двумя вращательными и одной поступательной кинематическими парами (рис. 1.6.б).

4.3) Шатун 4 и ползун 5 образуют группу Ассура2-го класса с двумя вращательными и одной поступательной кинематическими парами (рис. 1.6.в).

Таким образом, механизм входят одна группа Ассура1-го класса и две группы Ассура2-го класса.

5) Представленный механизм является плоским механизмом 2-го класса.