IX. Разные задачи из механики и физики

Пример 7.

Найти закон стационарного распределения температур в прямом круговом цилиндре (радиус основания 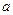, высота 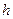), оба основания которого поддерживаются при постоянной нулевой температуре, а боковая поверхность имеет температуру, зависящую только от расстояния до нижнего основания цилиндра.

Решение. Поскольку рассматриваемая область – цилиндр, то задачу удобнее переформулировать в цилиндрических координатах 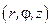. Из вида граничных условий заключаем, что задача является осесимметричной. Температура 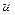не зависит от 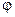и является функцией двух переменных 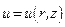и удовлетворяет уравнению Лапласа (которое тоже, естественно, записано в цилиндрических координатах). Таким образом, исходная задача сводится к решению следующей задачи:

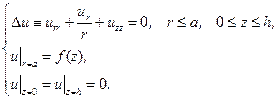
Полученное уравнение является уравнением в частных производных эллиптического типа и в совокупности с условиями на границе образует задачу Дирихле. Ее решение может быть получено методом разделения переменных.

Будем искать решение уравнения, удовлетворяющее граничным условиям 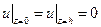в виде 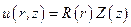. Разделяя переменные, имеем:

.

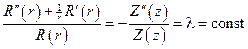Учитывая граничные условия, получаем, что функция 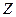является собственной функцией задачи Штурма–Лиувилля:

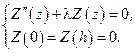
Как известно, собственные числа этой задачи 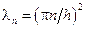, а соответствующие собственные функции 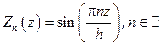. Для функции 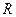получаем уравнение

,

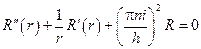решением которого являются функции Бесселя мнимого аргумента: 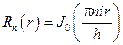. Так как рассматриваемое уравнение и граничные условия являются линейными, то ряд, составленный из найденных функций 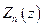и

,

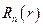
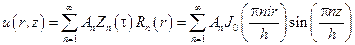при любых коэффициентах 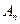также является решением уравнения, удовлетворяющим однородным краевым условиям. Для определения 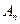используем граничное условие при :

.

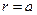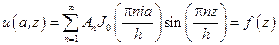Применяя теорему Стеклова, получаем:

.

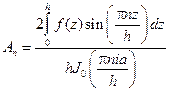Задание 12

Найти решение следующих задач, сведя их к уравнениям в частных производных с соответствующими начальными и краевыми условиями.

1. Найти закон стационарного распределения температур в прямом круговом цилиндре (радиус основания 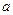, высота 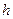), установленном на теплоизолирующем основании и нагреваемого потоком тепла плотностью 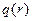( 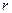– расстояние до оси цилиндра), поступающим через верхнее основание. Боковая поверхность цилиндра поддерживаются при постоянной нулевой температуре.

2. Найти закон стационарного распределения температур в прямом круговом цилиндре (радиус основания 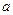, высота 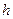), оба основания которого теплоизолированы, а боковая поверхность имеет температуру, зависящую только от расстояния до нижнего основания цилиндра.

3. Найти закон стационарного распределения температур в прямом круговом цилиндре (радиус основания 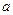, высота 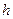), нижнее основание которого теплоизолировано, а через верхнее происходит конвективный обмен (по закону Ньютона) с окружающей средой, имеющей нулевую температуру. Боковая поверхность имеет температуру, зависящую только от расстояния до нижнего основания цилиндра.

4. Найти закон стационарного распределения температур в прямом круговом цилиндре (радиус основания 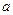, высота 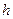), боковая поверхность которого теплоизолирована, нижнее основание поддеживается при постоянной нулевой температуре, а температура точек верхнего основания имеет радиальное распределение.

5. Найти закон стационарного распределения температур в прямом круговом цилиндре (радиус основания 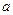, высота 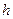), боковая поверхность которого поддерживается при постоянной температуре 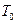, нижнее основание теплоизолировано, а температура точек верхнего основания имеет радиальное распределение.

6. Найти закон распределения тепла в шаре (радиуса 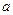), если ограничивающая его сфера поддерживается при постоянной нулевой температуре, а начальное распределение температур радиально.

7. Найти закон распределения тепла в шаре (радиуса 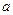), если ограничивающая его сфера теплоизолирована, а начальное распределение температур радиально.

8. Найти закон распределения тепла в шаре (радиуса 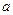), если через ограничивающую его сферу происходит конвективный теплообмен с окружающей средой, имеющей нулевую температуру. Начальное распределение температур радиально.

9. Найти закон распределения тепла в шаровом слое 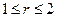, если обе ограничивающие его сферы поддерживаются при постоянной нулевой температуре, а начальное распределение температур задается равенством 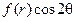(координаты сферические).

10. Однородный шар единичного радиуса имеет начальную температуру всех точек 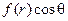(координаты сферические). Найти закон распределения температур в шаре в любой момент времени, если на поверхности шара поддерживается постоянная температура .

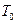11. Начальная температура однородного шарового слоя 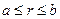(координаты сферические) зависит только от расстояния до центра шара. Найти распределение температур в слое в любой момент времени, если внутренняя и внешняя сферы поддерживаются при постоянных температурах 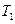и 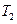соответственно.

12. Найти закон распределения температур в бесконечном цилиндрическом секторе 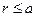, , 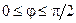, 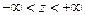если на поверхности 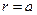и гранях 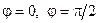поддерживается постоянная нулевая температура, а начальная температура равна 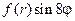(координаты цилиндрические).

13. Найти закон стационарного распределения температур внутри прямого кругового цилиндра (радиус основания 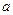, высота 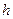), если на основаниях цилиндра поддерживается постоянная нулевая температура, а температура боковой поверхности 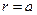равна .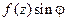

14. В однородном бесконечном круговом цилиндре радиуса 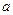начальная температура всех точек равна нулю. Ось цилиндра представляет собой тонкую стальную нить, которую, начиная с момента времени 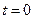, поддерживают при постоянной температуре 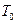. Найти распределение температур в цилиндре в любой момент времени, если его боковая поверхность теплоизолирована.

15. Найти закон распределения температур в бесконечной цилиндрической трубе радиуса 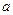, если начальное распределение температур радиально, а температура боковой поверхности 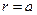постоянна и равна .

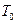16. Начальная температура однородного шарового слоя 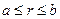(координаты сферические) зависит только от расстояния точки до начала координат. Внешняя сфера поддерживается при постоянной температуре 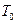, внутренняя сфера теплоизолирована. Найти закон распределения температур в слое в любой момент времени.

17. Дан однородный цилиндр (радиус основания 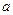, высота 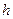), температура которого в начальный момент времени равна 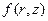(координаты цилиндрические). Основания цилиндра и его боковая поверхность поддерживаются при постоянной нулевой температуре. Найти закон распределения тепла внутри цилиндра в любой момент времени.

18. Однородный шар, ограниченный сферой 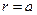, имеет начальную температуру всех точек равную нулю. Внутри шара, начиная с момента времени 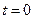, действует источник тепла с постоянной плотностью 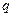. Найти распределение температур в шаре, если его поверхность имеет постоянную температуру .

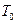19. Найти закон движения круглой однородной мембраны, если в начальный момент она представляет собой поверхность параболоида вращения 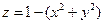, а начальные скорости равны нулю. Мембрана жестко закреплена на окружности 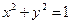, лежащей в плоскости .

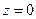20. Найти распределение температур в однородном шаре единичного радиуса, поверхность которого свободно охлаждается в среде, имеющей нулевую температуру (теплообмен происходит по закону Ньютона). Начальная температура шара равна 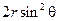(координаты сферические).

21. Найти стационарное распределение температур в шаровом слое 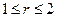, если температура внутреннего слоя равна 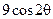, а внешнего – 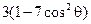(координаты сферические).

22. Найти стационарную температуру внутренних точек полусферы радиуса 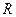, если сферическая поверхность поддерживается при постоянной температуре 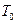, а основание полусферы – при нулевой температуре.

23. Найти стационарное распределение концентрации неустойчивого газа внутри бесконечного цилиндра кругового сечения, если на поверхности цилиндра поддерживается постоянная концентрация .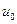

24. Найти собственные колебания мембраны, имеющей форму кольцевого сектора 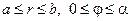со свободной границей.

25. Найти потенциал электростатического поля внутри цилиндрической коробки кругового сечения ( 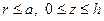), оба основания которой заземлены, а боковая поверхность заряжена до потенциала 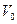. Определить напряженность поля на оси цилиндра.

Рекомендуемая литература

1. Тихонов А.Н. Уравнения математической физики / А.Н. Тихонов, А.А. Самарский. – М.: МГУ, 1999.
2. Владимиров В.С. Уравнения математической физики / В.С. Владимиров, В.В. Жаринов. – М.: Физматлит, 2003.
3. Будак Б.М. Сборник задач по математической физике / Б.М. Будак, А.А. Самарский, А.Н. Тихонов. – М.: Наука, 1978.
4. Владимиров В.С. Сборник задач по математической физике/ В.С. Владимиров, В.П. Михайлов и др. – М.: Наука, 1974.
5. Бицадзе А.В. Сборник задач по уравнениям математической физики. / А.В. Бицадзе, Д.Ф. Калиниченко – М.: Наука, 1985.
6. Пикулин В.П. Практический курс по уравнениям математической физики / В.П.Пикулин, С.И. Похожаев. – М.: МЦНМО, 2004.