IV. Решение волнового уравнения по формуле Д’Аламбера для бесконечной и полубесконечной струны
Пример 3.
Найти уравнение движения вынужденных колебаний полубесконечной струны со свободным левым концом, если в начальный момент времени струна имеет профиль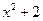 
, начальные скорости всех точек струны равны 
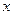, а плотность внешних сил (рассчитанных на единицу массы), которые действуют на струну, равна 
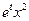. Натяжение струны равно ее линейной плотности.
Решение.
Уравнение движения струны в условиях задачи имеет вид:
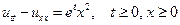. (4.1)
Это уравнение следует дополнить начальными условиями
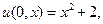
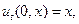(4.2)
и граничным условием на левом конце:
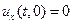. (4.3)
Таким образом, мы получили неоднородное волновое уравнение, для решения которого можно использовать либо интегральную формулу представления решения, либо метод подбора по правой части. В данном случае правая часть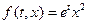 
имеет простой вид и позволяет сразу предположить вид частного решения уравнения (4.1): 
.
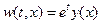Подставляя функцию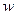 
в уравнение (4.1), получаем для 
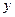уравнение 
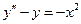, частное решение которого легко находится: 
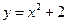. Следовательно, 
.
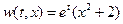Сделаем в уравнении (4.1), начальных условиях (4.2) и граничном условии (4.3) замену переменных
.
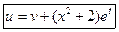Для функции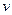 
получим следующую задачу:
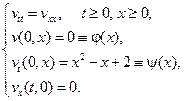
Учитывая вид граничного условия, продолжим функци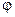и 
и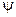 
на отрицательную ось четным образом: 
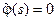при всех 
, 
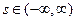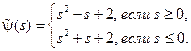
Применяя формулу Д' Аламбера, находим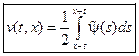 
.
При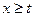 
получаем:
.
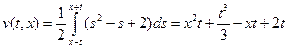При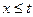 
, с учетом продолжения 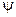, имеем: 
.
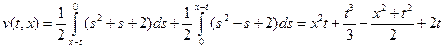Возвращаясь к функции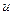 
, получаем решение исходной задачи:
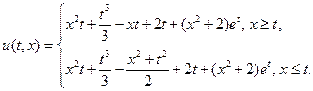
Задание 4.
Найти решения волновых уравнений, описывающих свободные колебания бесконечной или полубесконечной струны.
1. 
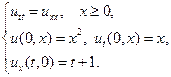
2. 
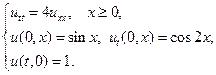
3. 
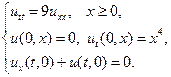
4. 
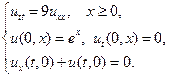
5. 
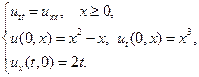
6. 
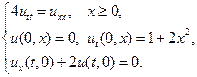
7. 
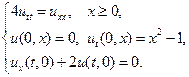
8. 
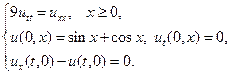
9. 
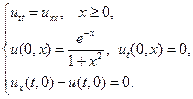
10. 
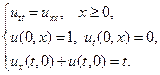
11. 
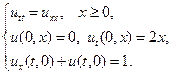
12. 
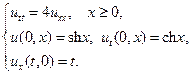
13. 
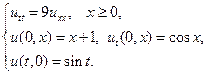
14. 
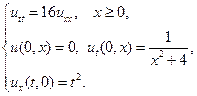
15. 
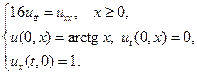
16. 
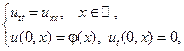
где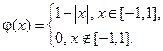 
Построить профиль струны в момент времени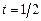 
.
17.
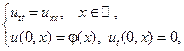
где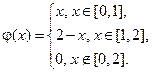 
Построить профиль струны в момент времени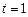 
.
18. 
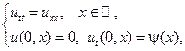
где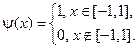 
Построить профиль струны в момент времени .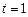
19.
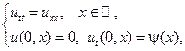
где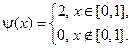 
Построить профиль струны в момент времени .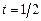
20.
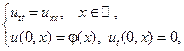
где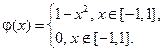 
Построить профиль струны в момент времени .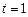
21. 
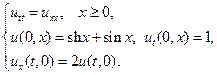
22. 
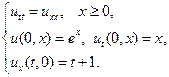
23.
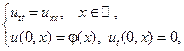
где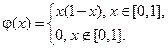 
Построить профиль струны в момент времени .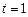
24. 
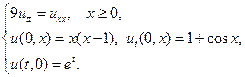
25.
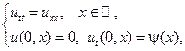
где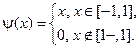 
Построить профиль струны в момент времени .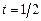
Задание 5.
Найти решения волновых уравнений, описывающих вынужденные колебания полубесконечной струны с заданными начальными условиями и граничным условием на левом конце.
1. 
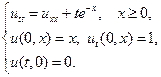
2. 
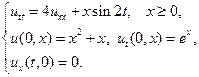
3. 
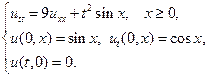
4. 
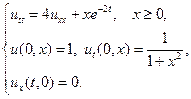
5. 
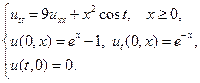
6. 
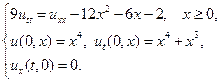
7. 
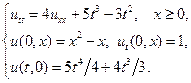
8. 
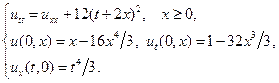
9. 
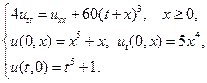
10. 
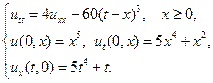
11. 
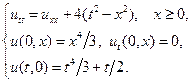
12. 
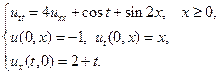
13. 
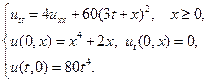
14. 
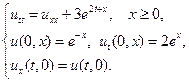
15. 
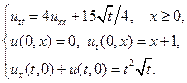
16. 
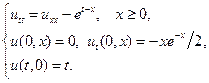
17. 
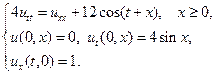
18. 
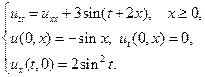
19. 
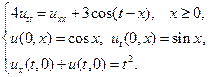
20. 
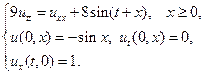
21. 
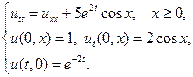
22. 
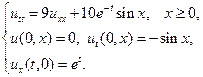
23. 
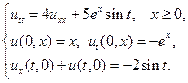
24. 
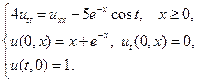
25. 
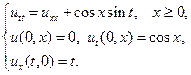
V. Метод Фурье для гиперболического и параболического уравнения на конечном отрезке
Решение задач на конечном отрезке (нагревание конечного стержня, движение конечной струны) потребовало принципиально иных идей и методов. Наиболее простой, и вместе с тем достаточно мощный метод решения таких задач – метод разделения переменных или метод Фурье.
Покажем, как работает этот метод при решении задачи о распределении тепла в конечном стержне.
Пример 4.
Найти закон распространения тепла в тонком однородном стержне длины π, имеющем коэффициент температуропроводности равный 2, если начальная температура всех точек стержня равна нулю, его левый конец поддерживается при постоянной температуре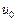 
, а правый конец и боковая поверхность теплоизолированы. Теплообмен несвободный: внутри стержня имеются источники и поглотители тепла, их интенсивность (в расчете на единицу массы стержня) равна 
.
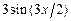Решение. Пусть стержень расположен вдоль отрезка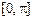 
, 
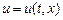– температура точки с координатой 
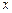в момент времени 
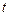. Уравнение теплопроводности в условиях задачи имеет вид
.
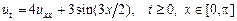Дополним уравнение начальным
,
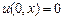и граничными условиями
, 
.
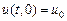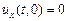Заменой переменных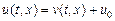 
преобразуем задачу к виду:
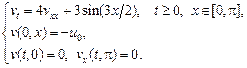(5.1)
Запишем соответствующую (5.1) задачу Штурма–Лиувилля:
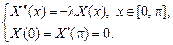(5.2)
Используя свойства собственных функций задачи Штурма–Лиувилля, заключаем, что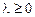 
. Легко видеть, что 
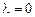не является собственным числом, т.к. в этом случае задача (5.2) имеет только тривиальные решения. Пусть 
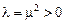, тогда общее решение уравнения (5.2) имеет вид 
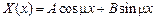. Из первого граничного условия находим, что 
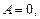из второго – что задача имеет нетривиальные решения только при 
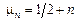, где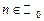 
. Следовательно, множество собственных чисел задачи (5.2) задается формулой 
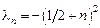, а соответствующие им собственные функции суть 
.
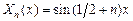Представим функцию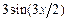 
в виде ряда, образованного ортогональной на 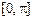системой 
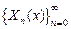. Из разложения
,
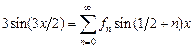в силу теоремы Стеклова, получаем, что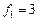 
, 
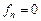при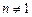 
.
Будем искать решение задачи (5.1) в виде ряда
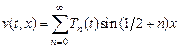, (5.3)
где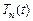 
– неизвестные, подлежащие определению функции. Заметим, что в силу (5.2) граничные условия для 
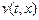выполняются автоматически. Подставим (5.3) в уравнение (5.1) и перенесем все слагаемые в левую часть:
.
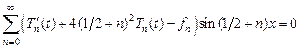Вновь применяя теорему Стеклова, получаем, что функции 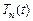должны удовлетворять уравнениям:
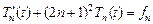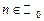, . (5.4)
Постоянные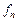 
были определены выше, и для нахождения 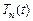нужно рассмотреть два случая.
· Если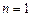 
, то уравнение (5.4) имеет вид 
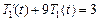, откуда следует, что 
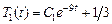, где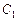 
– любое число.
· Если 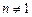, то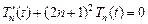 
, следовательно, 
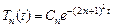, где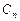 
– тоже произвольные числа.
Возвращаясь к представлению (5.3), получаем:
.
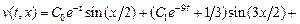
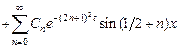Осталось найти постоянные 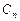. Для этого используем начальное условие:
.
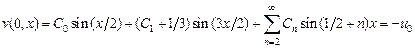Еще раз применяем теорему Стеклова и находим :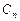
, 
,
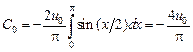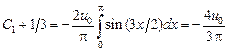и далее, при всех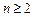 
, 
.
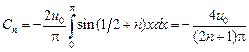Следовательно,
.
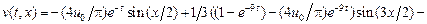
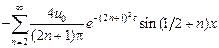Возвращаясь к функции 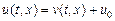, получаем решение исходной задачи:
.
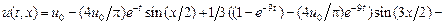
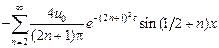Задание 6.
Применяя метод Фурье, найти решение следующих волновых уравнений на конечном отрезке.
1. 
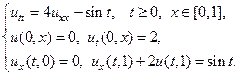
2. 
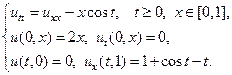
3. 
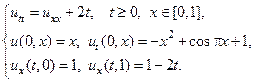
4. 
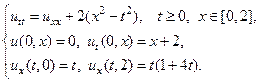
5. 
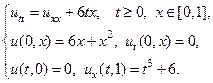
6. 
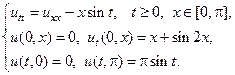
7. 
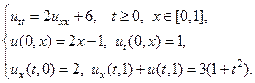
8. 
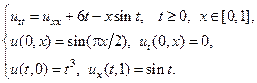
9. 
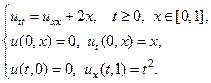
10. 
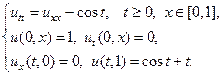
11. 
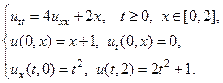
12. 
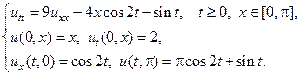
13. 
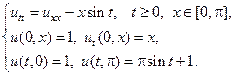
14. 
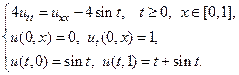
15. 
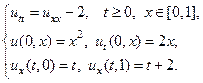
16. 
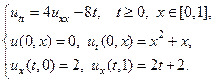
17. 
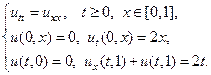
18. 
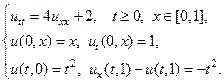
19. 
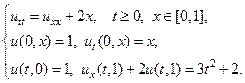
20. 
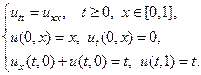
21. 
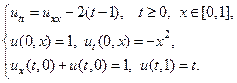
22. 
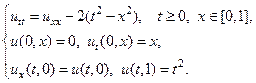
23. 
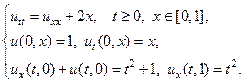
24. 
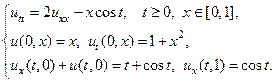
25. 
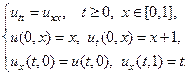
Задание 7.
Применяя метод Фурье, найти решение следующих уравнений теплопроводности на конечном отрезке.
1. 
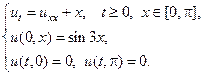
2. 
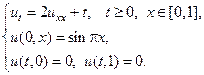
3. 
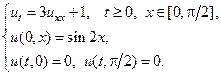
4. 
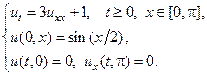
5. 
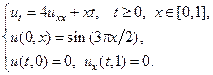
6. 
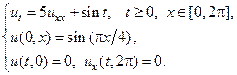
7. 
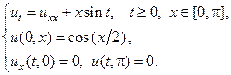
8. 
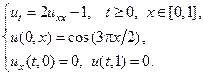
9. 
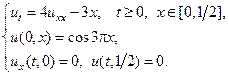
10. 
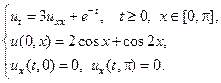
11. 
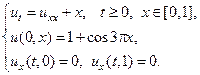
12. 
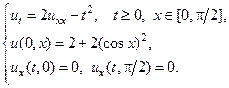
13. 
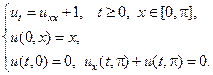
14. 
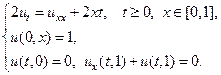
15. 
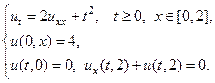
16. 
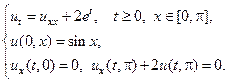
17. 
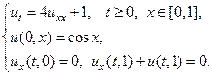
18. 
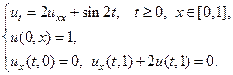
19. 
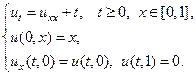
20. 
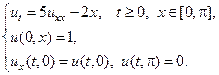
21. 
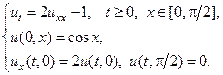
22. 
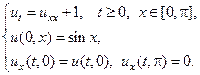
23. 
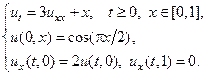
24. 
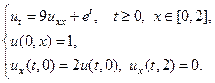
25. 