Условие параллельности прямой и плоскости

Если прямая параллельна плоскости, то векторы 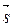и перпендикулярны (рисунок 16), поэтому 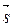∙ = 0, то есть

Ат + Вп + Ср = 0.

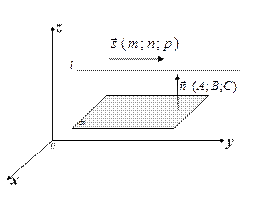
Рисунок 16 – Параллельность прямой и плоскости

Условие перпендикулярности прямой и плоскости

Если прямая перпендикулярна плоскости, то векторы 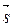и параллельны (рисунок 17), поэтому

.

Рисунок 17 – Перпендикулярность прямой и плоскости

Пересечение прямой и плоскости. Условие принадлежности прямой плоскости

Для того чтобы найти точку пересечения прямой 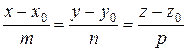с плоскостью Ах + Ву + Сz + D = 0, надо решить систему, составленную из этих уравнений. Проще всего это сделать, записав уравнение прямой в параметрическом виде:

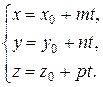
Подставляя эти выражения для х, у, z в уравнение плоскости, найдем значение t, при котором прямая и плоскость пересекаются. Возвращая найденное значение t в параметрические уравнения прямой, найдем координаты точки пересечения прямой и плоскости.

Если прямая параллельна плоскости и Ах₀ + Ву₀ + Сz₀ + D = 0, где (x₀, y₀, z₀) координаты точки М₀, принадлежащей прямой, то прямая лежит в плоскости.

Таким образом, одновременное выполнение равенств

является условием принадлежности прямой плоскости.

Вопросы для самопроверки

1 Записать формулу, по которой находится угол между прямой и плоскостью.

2 Записать условие параллельности прямой и плоскости.

3 Записать условие перпендикулярности прямой и плоскости.

4 Записать условия принадлежности прямой плоскости.

Пример 1. Составить уравнение плоскости, проходящей через прямую 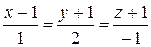и точку М₀(2; 0; 1).

Решение

Убедимся, что точка М₀ не принадлежит прямой:

.

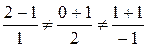Точка Р(1; – 1; – 1) принадлежит данной прямой, а 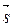= (1; 2; – 1) – направляющий вектор этой прямой (рисунок 18).

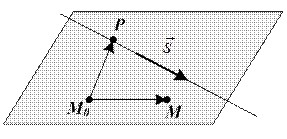
Рисунок 18 – Иллюстрация к примеру 1

Пусть М(х; у; z) – произвольная точка исходной плоскости, тогда векторы = (х – 2; у; z – 1), = (– 1; – 1; – 2) и = (1; 2; – 1) компланарны. Значит,

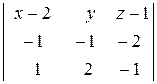= 0,

5(х – 2) – 3у – (z – 1) = 0.

Таким образом, уравнение исходной плоскости имеет вид

5х – 3у – z – 9 = 0.

Пример 2. Найти точку М₁ симметричную точке М(3; 1; – 1) относительно плоскости 3х + у + z – 20 = 0.

Решение

Нормальный вектор заданной плоскости 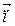= (3; 1; 1). Через точку М проведем перпендикуляр к плоскости (рисунок 19). Уравнение перпендикуляра имеет вид

.

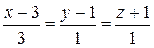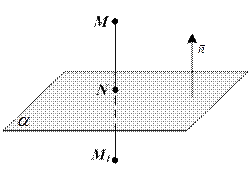
Рисунок 19 – Иллюстрация к примеру 2

Найдем координаты точки N пересечения прямой ММ₁ и плоскости

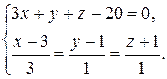
Запишем параметрические уравнения прямой

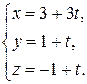
Подставим выражения для х, у, z в уравнение плоскости

3(3 + 3t) + (1 + t) + (– 1 + t) – 20 = 0.

После упрощения получим

11t = 11,

откуда

t = 1.

Подставив вместо t в параметрические уравнения прямой 1, найдем координаты проекции точки М на плоскость

x_N = 6, y_N = 2, z_N = 0,

то есть N(6; 2; 0).

Координаты точки М₁ найдем по формулам

, , ,

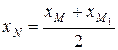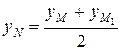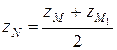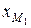= 2x_N – x_M = 9, 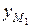= 2y_N – y_M = 3, = 2z_N – z_M = 1.

Таким образом, имеем М₁(9; 3; 1).

Пример 3. Найти уравнение проекции прямой 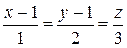на плоскость х + у + 2z – 5 = 0.

Решение

Через прямую l проведем плоскость β перпендикулярную плоскости α (рисунок 20). Тогда направляющий вектор = (1; 2; 3) прямой и нормальный вектор 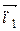= (1; 1; 2) данной плоскости перпендикулярны нормальному вектору 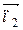β, следовательно, = × .

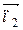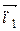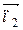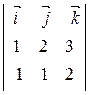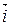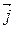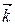= = + – = (1; 1; – 1).

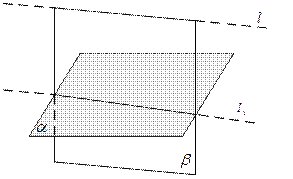
Рисунок 20 – Иллюстрация к примеру 3

Уравнение плоскости β запишем в виде

1(х – 1)+ 1(у – 1) – z = 0,

х + у – z – 2 = 0.

Искомую проекцию можно определить общими уравнениями, как линию пересечения двух плоскостей:

Пример 4.Найти расстояние от точки А(1; 3; 5) до прямой .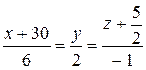

Решение

Так как по определению расстояние от точки А до прямой – это длина перпендикуляра АВ, проведенного из данной точки к данной прямой, то, определив координаты точки В, вычислим искомое расстояние как расстояние между точками А и В.

Таким образом, задача сводится к нахождению координат основания перпендикуляра, построенного из точки А к прямой. Точка В – это точка пересечения прямой с плоскостью, проходящей через точку А перпендикулярно к прямой. Уравнение этой плоскости имеет вид

6(х – 1)+ 2(у – 3) – (z – 5)= 0,

6х + 2у – z – 7 = 0.

Найдем координаты точки пересечения плоскости с прямой

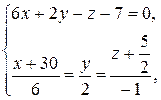
6(– 30 + 6t) + 2∙2t – (– 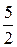– t) – 7 = 0,

41t – 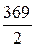= 0,

t = .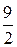

Точка пересечения В(– 3; 9; – 7). Найдем расстояние между точками А и В:

d = 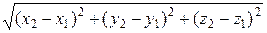= = 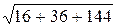14,

d = 14.

Задачи для самостоятельного решения

1Определить взаимное расположение прямой и плоскости:

а) 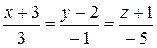, х – 2у + z – 15 = 0;

б) 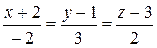, х + 2у – 2z + 6 = 0;

в) , 2х + 3у + z – 1 = 0;

(Ответ: а) прямая параллельна плоскости; б) прямая лежит в плоскости; в) (2; – 3; 6))

2Написать уравнение плоскости, проходящей через точку А(3; 4; 0) и прямую 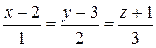. (Ответ: х – 2у + z + 5 = 0)

3Написать уравнение плоскости, проходящей через прямую 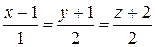и перпендикулярно плоскости 2х + 3у – z = 4. (Ответ: 8х – 5у + z – 11 = 0)

4Составить уравнение плоскости, проходящей через две прямые:

а) , ;

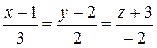б) , .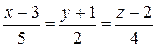

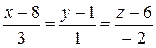(Ответ: а) 6х – 2у – 11z + 10 = 0; б) 8х – 22у + z – 48 = 0)

5Найти точку симметричную точке Р(4; 3; 10) относительно прямой 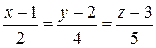. (Ответ: (2; 9; 6))

6Найти проекцию точки А(4; – 3; 1) на плоскость х + 2у – z – 3 = 0. (Ответ: (5; – 1; 0))

7Найти расстояние от точки А(7; 9; 7) до прямой 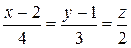. (Ответ: d = 14)

8Найти каноническое уравнение проекции прямой на плоскость х – у + 3z + 8 = 0. (Ответ: )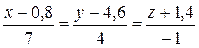

Список используемой литературы

1 Гурский Е.И. Основы линейной алгебры и аналитической геометрии / – 2-е изд. доп. – Минск: Выш. шк., 1982. – 272 с.

2 Гусак А.А. Справочное пособие по решению задач: аналитическая геометрия и линейная алгебра. – Минск: ТетраСистемс, 1998. – 228 с.

3 Письменный Д.Т. Конспект лекций по высшей математике: полный курс / – 9-е изд. – М.: Айрис-пресс, 2009.

4 Сборник задач по линейной алгебре и аналитической геометрии / под ред. В.Т. Воднева. – Минск: Выш. шк., 1990. – 288 с.

5 Сборник индивидуальных заданий по высшей математике: в 3 ч. Ч. 1 / под ред. А.П. Рябушко. – Минск: Выш. шк., 1990–1991.

Учебное издание

ВЫСШАЯ МАТЕМАТИКА

Методические указания

к решению задач по теме

«Аналитическая геометрия на плоскости и в пространстве»

для студентов всех форм обучения и специальностей

Составители:

ШендриковаОльга Александровна

Юрченко Ирина Викторовна

Редактор А.А. Щербакова

Технический редактор Н.Г.Тверская

Подписано в печать Формат 60×84 1 ∕ 16.

Бумага офсетная. Гарнитура Таймс. Ризография.

Усл.печ.л. Уч.-изд.

Тираж экз. Заказ .

Учреждение образования

«Могилевский государственный университет продовольствия».

Свидетельство о государственной регистрации издателя, изготовителя, распространителя печатных изданий № 1/272 от 04.04.2014 г.

Пр-т Шмидта, 3, 212027, Могилев.

Отпечатано в учреждении образования

«Могилевский государственный университет продовольствия».

Пр-т Шмидта, 3, 212027, Могилев.