Уравнение плоскости, проходящей через три данные точки

Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Составим уравнение плоскости, которая проходит через три данные точки М₁(х₁; у₁; z₁), М₂(х₂; у₂; z₂), М₃(х₃; у₃; z₃). Возьмем на плоскости произвольную точку М(х; у; z) и составим векторы 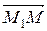= (х – х₁; у – у₁; z – z₁), 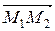= (х₂ – х₁; у₂– у₁; z₂ – z₁), = (х₃ – х₁; у₃– у₁; z₃ – z₁). Эти векторы лежат в одной плоскости, следовательно, они компланарны. 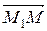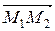Используя условие компланарности трех векторов (их смешанное произведение равно нулю), получим ∙ ∙ = 0, то есть

= 0. (3.5)

Уравнение (3.5) называется уравнением плоскости, проходящей через три данные точки.

Взаимное расположение плоскостей в пространстве

Угол между плоскостями

Пусть даны две плоскости

А₁х + В₁у + С₁z + D₁ = 0,

А₂х + В₂у + С₂z + D₂ = 0.

За угол между плоскостями принимаем угол φ между любыми двумя перпендикулярными к ним векторами (что дает два угла, острый и тупой, дополняющих друг друга до π). Так как нормальные векторы плоскостей 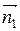= (А₁, В₁, С₁) и 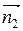= (А₂, В₂, С₂) перпендикулярны им, то получаем

cosφ =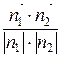

или

cosφ = .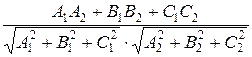

Условие перпендикулярности двух плоскостей

Если две плоскости перпендикулярны, то нормальные векторы этих плоскостей также перпендикулярны и их скалярное произведение равно нулю: 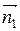∙ 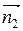= 0. Значит, условием перпендикулярности двух плоскостей является

А₁А₂ + В₁В₂ + С₁С₂ = 0.

Условие параллельности двух плоскостей

Если плоскости параллельны, то будут параллельны и их нормальные векторы. Тогда одноименные координаты нормальных векторов пропорциональны. Значит, условием параллельности плоскостей является

= = .

Расстояние от точки М₀(x₀, y₀, z₀) до плоскости Ах + Ву + Сz + D = 0.

Расстоянием от точки М₀(x₀, y₀, z₀) до плоскости Ах + Ву + Сz + D = 0 называется длина перпендикуляра, проведенного из этой точки на плоскость, и находится по формуле

d = .

Пример 1. Составить уравнение плоскости, проходящей через точку Р(– 1, 2, 7) перпендикулярно вектору 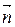= (3, – 1, 2).

Решение

Согласно уравнению (3.1) получаем

3(х + 1) – (у – 2) + 2(z – 7) = 0,

3х – у + 2z – 9 = 0.

Пример 2.Составить уравнение плоскости, проходящей через точку М(2; – 3; – 7) параллельно плоскости 2х – 6у – 3z + 5 = 0.

Решение

Вектор = (2; – 6; – 3) перпендикулярный к плоскости перпендикулярен и к параллельной плоскости. Значит, искомая плоскость проходит через точку М(2; – 3; – 7) перпендикулярно вектору = (2; – 6; – 3). Найдем уравнение плоскости по формуле (3.1):

2(х – 2) – 6(у + 3) – 3(z + 7) = 0,

2х – 6у – 3z – 43 = 0.

Пример 3.Найти уравнение плоскости, проходящей через точки М₁(2; 3; – 1) и М₂(1; 5; 3)перпендикулярно к плоскости 3х – у + 3z + 15 = 0.

Решение

Вектор = (3; – 1; 3) перпендикулярный к заданной плоскости будет параллелен искомой плоскости. Таким образом, плоскость проходит через точки М₁ и М₂ параллельно вектору .

Пусть М(x; y; z) произвольная точка плоскости, тогда векторы 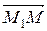= (х – 2; у – 3; z + 1), 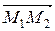= (– 1; 2; 4), = (3; – 1; 3) компланарны, значит их смешанное произведение равно нулю:

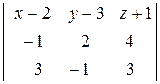= 0.

Вычислим определитель разложением по элементам первой строки:

(х – 2) 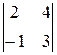– (у – 3) 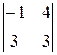+ (z + 1) 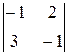= 0,

10(х – 2) – (– 15)(у – 3) + (– 5)(z + 1) = 0,

2(х – 2) + 3(у – 3) – (z + 1) = 0,

2х + 3у – z – 14 = 0 – уравнение плоскости.

Пример 4.Составить уравнение плоскости, проходящей через начало координат перпендикулярно к плоскостям 2х – у + 5z + 3 = 0 и х + 3у – z – 7 = 0.

Решение

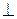
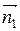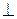
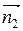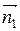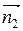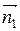Пусть – нормальный вектор искомой плоскости. По условию плоскость перпендикулярна данным плоскостям, значит и , где = (2; – 1; 5), = (1; 3; – 1). Значит, в качестве вектора можно взять векторное произведение векторов и 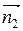, то есть = × .

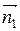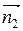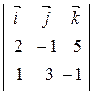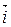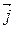= = – 14 + 7 + 7 .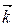

Подставив координаты вектора в уравнение плоскости, проходящей через начало координат Ах + Ву + Сz = 0, получим

– 14х + 7у + 7z = 0,

или

2х – у – z = 0.

Вопросы для самопроверки

1 Записать общее уравнение плоскости.

2 Каков геометрический смысл коэффициентов при х, у, z в общем уравнении плоскости?

3 Записать уравнение плоскости, проходящей через точку М₀(x₀; y₀; z₀) перпендикулярно к вектору 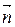= (А; В; С).

4 Записать уравнение плоскости в отрезках по осям и указать геометрический смысл входящих в него параметров.

5 Записать уравнение плоскости, проходящей через точки М₁(х₁; у₁; z₁), М₂(х₂; у₂; z₂), М₃(х₃; у₃; z₃).

6 Записать формулу, по которой находят угол между двумя плоскостями.

7 Записать условия параллельности двух плоскостей.

8 Записать условие перпендикулярности двух плоскостей.

9 Записать формулу, по которой вычисляется расстояние от точки до плоскости.

Задачи для самостоятельного решения

1Составить уравнение плоскости, проходящей через точку М(2; – 1; 1) перпендикулярно вектору 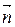= (1; – 2; 3). (Ответ: х – 2у + 3z – 7 = 0)

2Точка Р(1; – 2; – 2) является основанием перпендикуляра, проведенного из начала координат к плоскости. Составить уравнение этой плоскости. (Ответ: х – 2у – 2z – 9 = 0)

3Даны две точки М₁(2; – 1; 3) и М₂(– 1; 2; 4). Составить уравнение плоскости, проходящей через точку М₁ перпендикулярно вектору 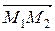. (Ответ: 3х – 3у – z – 6 = 0)

4Составить уравнение плоскости, проходящей через три точки М₁(3; – 1; 2), М₂(4; – 1; – 1), М₃(2; 0; 2). (Ответ: 3х + 3у + z – 8 = 0)

5Составить уравнение плоскости, проходящей через точки М₁(3; – 1; 2) и М₂(2; 1; 3) параллельно вектору 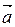= (3; – 1; 4). (Ответ: 9х + 7у – 5z – 10 = 0)

6Составить уравнение плоскости, проходящей через точку М₁(2; 3; – 4) параллельно векторам 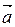= (3; 1; – 1) и = (1; – 2; 1). (Ответ: х + у + 7z + 14 = 0)

7Составить уравнение плоскости, проходящей через точку М(1; – 1; 1) перпендикулярно плоскостям 2х – у + z – 1 = 0 и х + 2у – z + 1 = 0. (Ответ: х – 3у – 5z + 1 = 0)

8Составить уравнение плоскости, проходящей через точки М₁(1; 0; 1) и М₂(1; 2; – 3) перпендикулярно плоскости х – у + z – 1 = 0. (Ответ: х + 2у + z – 2 = 0)

9Найти угол между плоскостями 4х – 5у + 3z – 1 = 0 и х – 4у – z + 9 = 0. (Ответ: φ = arccos0,7)

10Найти расстояние от точки М(2; – 1; – 1) до плоскости 16х – 12у + 15z – 4 = 0. (Ответ: d = 1)

11Найти точку пересечения трех плоскостей 5х + 8у – z – 7 = 0, х + 2у + 3z – 1 = 0, 2х – 3у + 2z – 9 = 0. (Ответ: (3; – 1; 0))

12Составить уравнение плоскости, которая проходит через точки М₁(1; – 2; 6) и М₂(5; – 4; 2) и отсекает равные отрезки на осях Ох и Оу. (Ответ: 4х + 4у + z – 2 = 0)

13Найти расстояние между плоскостями х + 2у – 2z + 2 = 0 и 3х + 6у – 6z – 4 = 0. (Ответ: d = )