Двоичные функции одного аргумента
Лекция № 2
Асинхронные потенциальные и синхронные автоматы
Текст лекции по дисциплине: «Цифровые устройства и микропроцессоры»
КАЛИНИНГРАД
Г
Содержание
Введение.
Учебные вопросы (основная часть):
1. Дискретные автоматы
2. Функциональные полные системы двоичных функций
Заключение
Литература:
Л1. А.К.Нарышкин «Цифровые устройств и микропроцессоры»: учеб. пособие для студ. Высш. Учебн. Заведений/ А. К. Нарышкин, 2 – е изд. - Издательский центр «Академия», 2008г. с. 52-76
Л2. Ю.Ф. Опадчий, О.П. Глудкин, А.И. Гуров «Аналоговая и цифровая электроника», М.- Горячая линия- Телеком, 2000г. с. 509-513
Л9. Б.А.Калабеков «Цифровые устройства и микропроцессорные системы», М.: «Горячая линия - телеком», 2000 г. с. 4-21, 204-206
Учебно-материальное обеспечение:
1. Полилюкс
2. Слайды
Текст лекции
Введение
В основе построения ЦС лежат простейшие схемы, выполняющие логические операции над электрическими сигналами, представленными в виде специальных кодов. Такие сигналы представляются в виде наличия или отсутствия большого уровня напряжения, т. получили название двоичных сигналов.
1. Дискретные автоматы
Обработка цифровой информации в ЭВМ производится электронными схемами—цифровыми устройствами (ЦУ), которые работают с двоичными кодами , получивишими название цифровые автоматы.
Термин «автомат» подразумевает устройство, выполняющее некоторые функции без непосредственного участия человека. Термин «автомат» обозначает математическую модель реальных автоматов
Автоматом называют любое устройство, осуществляющее преобразование информации.
Классификация:
1. В зависимости от типа сигналов, используемых для представления информации в автомате, и характера работы автомата во времени автоматы делят на два класса:
- автоматы непрерывного действия;
- автоматы дискретного действия (дискретные автоматы).
В автоматах непрерывного действия используются непрерывные по уровню сигналы. Время рассматривается как непрерывная величина.
В дискретных автоматах используются дискретные по уровню сигналы. Время рассматривается как дискретная величина, т.е. выделяются отдельные дискретные моменты времени, в которые сигналы в автомате могут принимать отличные от нуля значения или в которые возможны изменения значений сигналов в автомате.
2. В зависимости от характера преобразования информации во времени дискретные автоматы делятся на
- синхронные;
- асинхронные.
В синхронном дискретном автомате возможны 2 способа изменения значений уровня сигналов:
1). Изменения по уровню сигналов возможны лишь в отдельные фиксированные моменты времени, в промежутках изменения, значения всех сигналов в автомате сохраняются неизменными. При этом считается, что изменения происходят за бесконечно малый промежуток времени. Время, выражаемое в номерах интервалов, называется автоматным временем.
На Рис. 1, а изображен график изменения дискретного по уровню сигнала U в функции автоматного времени t.
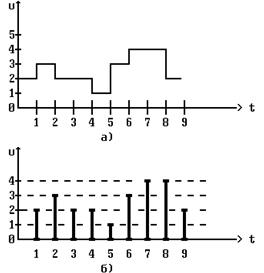
Рис. 1 Изменение дискретного по уровню сигнала в функции автоматного времени
2). Сигналы могут принимать отличные от нуля значения лишь в отдельные фиксированные моменты времени. В данном случае номеруются не интервалы времени, а моменты времени, и автоматное время выражается в номерах моментов времени (Рис. 1, б).
В синхронном дискретном автомате как при использовании непрерывных во времени сигналов (Рис. 1, а), так и при использовании дискретных во времени сигналов (Рис. 1, б) моменты автоматного времени, в которые происходят изменения сигналов или в которые существуют сигналы, разделены одинаковыми интервалами времени длительностью t, получившими название тактов. В реальном автомате эти моменты времени задаются с помощью специального устройства, называемого генератором тактовых сигналов.
В асинхронных дискретных автоматах моменты автоматного времени не задаются принудительно с помощью генератора и могут занимать любое положение во времени.
3. По зависимости сигналов на m выходах от сигналов на n входах.
1). Значения сигналов на выходах автомата в данный момент времени зависят только от значений сигналов на входах в тот же момент времени:
yj(t) = Fj[xi(t)]; i=1,..., n; j=1,..., m.
Такой автомат называется автоматом без памяти или комбинационной схемой (Рис. 2, а), что тоже самое - логическая схема.
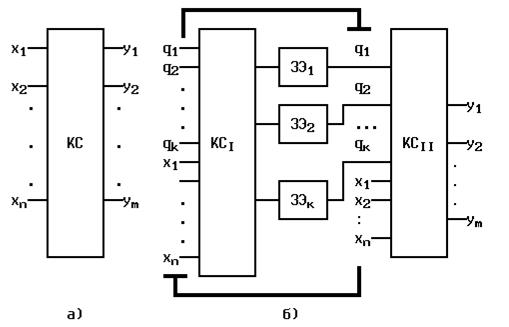
Рис. 2 Дискретные автоматы: а - автомат без памяти, б - автомат с памятью
2). Значения сигналов на выходах автомата в данный момент времени зависят от значений сигналов на входах автомата в этот же момент времени и предшествующие моменты времени:
yj(t)=Fj[xi(t), xi(t-1),..., xi(0)]; i=1,..., n, j=1,..., m.
Такой автомат называется автоматом с памятью (Рис. 2, б).
Очевидно, что автомат без памяти представляет собой частный случай автомата с памятью.
Значения выходных сигналов в автомате с памятью в любой момент времени зависят от значений входных сигналов в конечное число предшествующих моментов автоматного времени. Поэтому дискретные автоматы с памятью иногда называют конечными автоматами. На практике широкое применение нашли автоматы с памятью, значения выходных сигналов которых зависят от значений сигналов на входах в тот же и предшествующий моменты времени. В понятие конечности автомата входят также конечность числа значений входных и выходных сигналов.
Отдельные значения дискретных по уровню сигналов в дискретных автоматах кодируются буквами некоторого алфавита. В ЦС, как правило, для кодирования сигналов используется алфавит, состоящий из двух букв (цифр) - нуля и единицы. Автоматы с кодированием значений сигналов цифрами (0 и 1) часто называют цифровыми автоматами.
Для описания работы цифрового автомата используют специальный математический аппарат - аппарат двоичных функций. В теории двоичных функций рассматриваются двоичные функции двоичных аргументов и двоичные функции, аргументы которых могут принимать более чем два значения. Математический аппарат, в котором используются двоичные функции двоичных аргументов, называется исчислением высказываний или алгеброй логики или булевой алгеброй. Математический аппарат, в котором используются двоичные функции недвоичных аргументов, называется исчислением предикатов.
Таким образом, автомат это любое устройство, осуществляющее преобразование информации. Чаще применяются цифровые автоматы, основой работы которых является алгебра логики.
2. Функциональные полные системы двоичных функций
Понятие о двоичных функциях
Алгебра логики оперирует следующими понятиями:
1). Переменная, которая может принимать два значения (0 и 1), называется двоичной переменной.
2). Двоичная переменная, значение которой зависит от значений других двоичных переменных аргументов, называется двоичной функцией (булевой функцией, переключательной функцией или функцией алгебры логики).
При наличии n двоичных аргументов существует 2n различных наборов их значений. Для образования всех 2n наборов значений n аргументов удобно аргументы рассматривать как разряды n-разрядного двоичного целого числа. Крайнему справа разряду (x0) приписывается вес 20, а крайнему слева разряду (хn-1) - вес 2n-1. При этом наборы значений аргументов могут рассматриваться как двоичные коды чисел от 0 до 2n-1 и образовываться в порядке возрастания. Число, двоичный код которого образуется набором значений аргументов, называется номером набора. (Набор это конкретная комбинация, в которой логические переменные принимают конкретные значения).
Для задания функции нужно каждому из 2n наборов значений аргументов поставить в соответствие значение функции (0 или 1) т.е. нужно образовать 2n- разрядное слово. Число разных слов будет равно 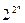 . Таким образом, всего от n аргументов может быть задано N =
. Таким образом, всего от n аргументов может быть задано N = 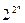 различных двоичных функций.
различных двоичных функций.
Двоичные функции, значения которых определены для всех наборов значений аргументов, называются полностью определенными, в противном случае они называются частично определенными двоичными функциями.
Процесс определения значения двоичной функции по значениям ее аргументов называется логической операцией. Простые логические операции над двоичными элементами реализуются элементарными автоматами без памяти или логическими элементами.
Лекция № 2
Асинхронные потенциальные и синхронные автоматы
Текст лекции по дисциплине: «Цифровые устройства и микропроцессоры»
КАЛИНИНГРАД
Г
Содержание
Введение.
Учебные вопросы (основная часть):
1. Дискретные автоматы
2. Функциональные полные системы двоичных функций
Заключение
Литература:
Л1. А.К.Нарышкин «Цифровые устройств и микропроцессоры»: учеб. пособие для студ. Высш. Учебн. Заведений/ А. К. Нарышкин, 2 – е изд. - Издательский центр «Академия», 2008г. с. 52-76
Л2. Ю.Ф. Опадчий, О.П. Глудкин, А.И. Гуров «Аналоговая и цифровая электроника», М.- Горячая линия- Телеком, 2000г. с. 509-513
Л9. Б.А.Калабеков «Цифровые устройства и микропроцессорные системы», М.: «Горячая линия - телеком», 2000 г. с. 4-21, 204-206
Учебно-материальное обеспечение:
1. Полилюкс
2. Слайды
Текст лекции
Введение
В основе построения ЦС лежат простейшие схемы, выполняющие логические операции над электрическими сигналами, представленными в виде специальных кодов. Такие сигналы представляются в виде наличия или отсутствия большого уровня напряжения, т. получили название двоичных сигналов.
1. Дискретные автоматы
Обработка цифровой информации в ЭВМ производится электронными схемами—цифровыми устройствами (ЦУ), которые работают с двоичными кодами , получивишими название цифровые автоматы.
Термин «автомат» подразумевает устройство, выполняющее некоторые функции без непосредственного участия человека. Термин «автомат» обозначает математическую модель реальных автоматов
Автоматом называют любое устройство, осуществляющее преобразование информации.
Классификация:
1. В зависимости от типа сигналов, используемых для представления информации в автомате, и характера работы автомата во времени автоматы делят на два класса:
- автоматы непрерывного действия;
- автоматы дискретного действия (дискретные автоматы).
В автоматах непрерывного действия используются непрерывные по уровню сигналы. Время рассматривается как непрерывная величина.
В дискретных автоматах используются дискретные по уровню сигналы. Время рассматривается как дискретная величина, т.е. выделяются отдельные дискретные моменты времени, в которые сигналы в автомате могут принимать отличные от нуля значения или в которые возможны изменения значений сигналов в автомате.
2. В зависимости от характера преобразования информации во времени дискретные автоматы делятся на
- синхронные;
- асинхронные.
В синхронном дискретном автомате возможны 2 способа изменения значений уровня сигналов:
1). Изменения по уровню сигналов возможны лишь в отдельные фиксированные моменты времени, в промежутках изменения, значения всех сигналов в автомате сохраняются неизменными. При этом считается, что изменения происходят за бесконечно малый промежуток времени. Время, выражаемое в номерах интервалов, называется автоматным временем.
На Рис. 1, а изображен график изменения дискретного по уровню сигнала U в функции автоматного времени t.

Рис. 1 Изменение дискретного по уровню сигнала в функции автоматного времени
2). Сигналы могут принимать отличные от нуля значения лишь в отдельные фиксированные моменты времени. В данном случае номеруются не интервалы времени, а моменты времени, и автоматное время выражается в номерах моментов времени (Рис. 1, б).
В синхронном дискретном автомате как при использовании непрерывных во времени сигналов (Рис. 1, а), так и при использовании дискретных во времени сигналов (Рис. 1, б) моменты автоматного времени, в которые происходят изменения сигналов или в которые существуют сигналы, разделены одинаковыми интервалами времени длительностью t, получившими название тактов. В реальном автомате эти моменты времени задаются с помощью специального устройства, называемого генератором тактовых сигналов.
В асинхронных дискретных автоматах моменты автоматного времени не задаются принудительно с помощью генератора и могут занимать любое положение во времени.
3. По зависимости сигналов на m выходах от сигналов на n входах.
1). Значения сигналов на выходах автомата в данный момент времени зависят только от значений сигналов на входах в тот же момент времени:
yj(t) = Fj[xi(t)]; i=1,..., n; j=1,..., m.
Такой автомат называется автоматом без памяти или комбинационной схемой (Рис. 2, а), что тоже самое - логическая схема.

Рис. 2 Дискретные автоматы: а - автомат без памяти, б - автомат с памятью
2). Значения сигналов на выходах автомата в данный момент времени зависят от значений сигналов на входах автомата в этот же момент времени и предшествующие моменты времени:
yj(t)=Fj[xi(t), xi(t-1),..., xi(0)]; i=1,..., n, j=1,..., m.
Такой автомат называется автоматом с памятью (Рис. 2, б).
Очевидно, что автомат без памяти представляет собой частный случай автомата с памятью.
Значения выходных сигналов в автомате с памятью в любой момент времени зависят от значений входных сигналов в конечное число предшествующих моментов автоматного времени. Поэтому дискретные автоматы с памятью иногда называют конечными автоматами. На практике широкое применение нашли автоматы с памятью, значения выходных сигналов которых зависят от значений сигналов на входах в тот же и предшествующий моменты времени. В понятие конечности автомата входят также конечность числа значений входных и выходных сигналов.
Отдельные значения дискретных по уровню сигналов в дискретных автоматах кодируются буквами некоторого алфавита. В ЦС, как правило, для кодирования сигналов используется алфавит, состоящий из двух букв (цифр) - нуля и единицы. Автоматы с кодированием значений сигналов цифрами (0 и 1) часто называют цифровыми автоматами.
Для описания работы цифрового автомата используют специальный математический аппарат - аппарат двоичных функций. В теории двоичных функций рассматриваются двоичные функции двоичных аргументов и двоичные функции, аргументы которых могут принимать более чем два значения. Математический аппарат, в котором используются двоичные функции двоичных аргументов, называется исчислением высказываний или алгеброй логики или булевой алгеброй. Математический аппарат, в котором используются двоичные функции недвоичных аргументов, называется исчислением предикатов.
Таким образом, автомат это любое устройство, осуществляющее преобразование информации. Чаще применяются цифровые автоматы, основой работы которых является алгебра логики.
2. Функциональные полные системы двоичных функций
Понятие о двоичных функциях
Алгебра логики оперирует следующими понятиями:
1). Переменная, которая может принимать два значения (0 и 1), называется двоичной переменной.
2). Двоичная переменная, значение которой зависит от значений других двоичных переменных аргументов, называется двоичной функцией (булевой функцией, переключательной функцией или функцией алгебры логики).
При наличии n двоичных аргументов существует 2n различных наборов их значений. Для образования всех 2n наборов значений n аргументов удобно аргументы рассматривать как разряды n-разрядного двоичного целого числа. Крайнему справа разряду (x0) приписывается вес 20, а крайнему слева разряду (хn-1) - вес 2n-1. При этом наборы значений аргументов могут рассматриваться как двоичные коды чисел от 0 до 2n-1 и образовываться в порядке возрастания. Число, двоичный код которого образуется набором значений аргументов, называется номером набора. (Набор это конкретная комбинация, в которой логические переменные принимают конкретные значения).
Для задания функции нужно каждому из 2n наборов значений аргументов поставить в соответствие значение функции (0 или 1) т.е. нужно образовать 2n- разрядное слово. Число разных слов будет равно 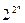 . Таким образом, всего от n аргументов может быть задано N =
. Таким образом, всего от n аргументов может быть задано N = 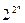 различных двоичных функций.
различных двоичных функций.
Двоичные функции, значения которых определены для всех наборов значений аргументов, называются полностью определенными, в противном случае они называются частично определенными двоичными функциями.
Процесс определения значения двоичной функции по значениям ее аргументов называется логической операцией. Простые логические операции над двоичными элементами реализуются элементарными автоматами без памяти или логическими элементами.
Двоичные функции одного аргумента
Известно, что от одного двоичного аргумента x может быть образовано четыре разных двоичных функций yj = Fj(x). Значения этих функций приведены в табл. 1.
Таблица 1
n = 1
| X | y0 | y1 | y2 | y3 | ||||
| 21 | ||||||||
| 21 | 20 | |||||||
N = 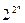 = 4 = 4 | ||||||||
Функция y0 сохраняет нулевое значение, а функция y3 - единичное значение при любом значении аргумента. Двоичная функция, сохраняющая нулевое или единичное значение при любом наборе значений аргументов, называется соответственно константой нуля (y0=0) или константой единицы (y3=1).
Функция y1 принимает значение, равное значению ее аргумента. Такая функция y1=x называется тавтологией. Ее реализует логический элемент повторитель, условное графическое обозначение которого приведено на Рис. 3, а.
Функция y2 принимает значение, противоположное значению ее аргумента. Такая функция называется инверсией. Операция отыскания значения инверсии по заданному значению ее аргумента называется операцией отрицания или операцией НЕ. Для обозначения операции отрицания используется запись следующего вида:
y = 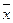 .
.
Произносится: y равно НЕ x. Функция инверсия реализуется логическим элементом - инвертором, УГО которого приведено на Рис. 3, б.
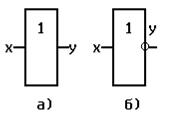
Рис. 3 Элементарные автоматы без памяти (двоичные функции одного аргумента)
