Структурная и приведенная формы моделей

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений вида:

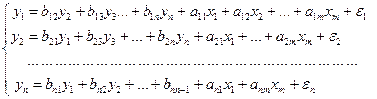(9.1)

Система взаимозависимых уравнений (9.1) получила название система совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные у одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели.

Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные обозначаются в системе одновременных уравнений как y. Это зависимые переменные, число которых равно числу уравнений в системе.

Экзогенные переменные обозначаются обычно как x. Это предопределённые переменные, влияющие на эндогенные переменные, но не зависящие от них.

Простейшая структурная форма модели (9.1) имеет вид:

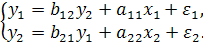
Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, в других – как экзогенные переменные.

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

Структурная форма модели в правой части содержит при эндогенных и экзогенных переменных коэффициенты b_i и a_j (b_i – коэффициент при эндогенной переменной, a_j - коэффициент при экзогенной переменной), которые называются структурные коэффициенты модели.

Использование МНК для оценивания структурных коэффициентов модели даёт, как принято считать в теории, смещённые и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

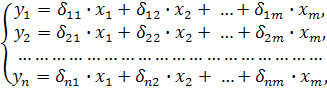
где 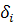– коэффициенты приведенной формы модели.

По виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным методом наименьших квадратов. Применяя МНК, можно оценить 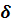,а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели 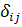через коэффициенты структурной модели (a_j и b_i ).

Для упрощения в модель не введены случайные переменные.

Для структурной модели вида:

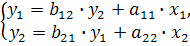(9.2)

Приведенная форма модели имеет вид:

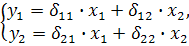(9.3)

в которой 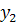из первого уравнения структурной модели можно выразить следующим образом:

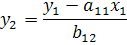
Тогда система одновременных уравнений будет приведена как

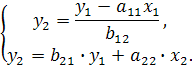
Отсюда имеем равенство:

или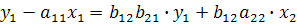

Тогда: +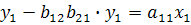

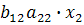
Или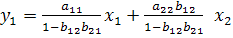

Т.о., мы представили первое уравнение структурной формы модели в виде уравнения приведенной формы модели:

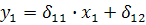
Из уравнения следует, что коэффициенты приведенной модели представляют собой нелинейные соотношения коэффициентов структурной формы модели, т.е.

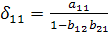и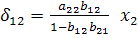

Аналогично можно показать, что коэффициенты приведенной формы модели второго уравнения системы ( 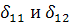) также нелинейно связаны с коэффициентами структурной модели. Для этого выразим переменную 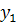из второго структурного уравнения модели как

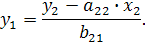
Запишем это выражение 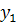в левой части первого уравнения структурной формы модели 1):

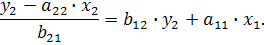
Отсюда: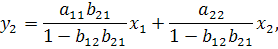

что соответствует уравнению приведенной формы модели:

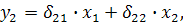
т.е. 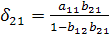и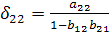

Эконометрические модели обычно включают в систему не только уравнения, отражающие взаимосвязи между отдельными переменными, но и выражения тенденции развития явления, а также разного рода тождества. Например, Т. Хаавелмо в 1947 г., исследуя линейную зависимость потребления (с) от дохода (у), предложил одновременно учитывать тождество дохода. В этом случае модель имеет вид:

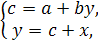
Где a и b – параметры линейной зависимости с от у;

х – инвестиции в основной капитал и в запасы экспорта и импорта.

Оценки параметров должны учитывать тождество дохода в отличие от параметров обычной линейной регрессии.

В этой модели две эндогенные переменные – с и у и одна экзогенная переменная х. система приведенных уравнений составит:

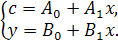
Она позволяет получить значения эндогенной переменной с через переменную х. рассчитав коэффициенты приведенной формы модели (А₀, А₁, В₀, В₁), можно перейти к коэффициентам структурной модели а и b, подставив в первое уравнение приведенной формы выражение переменной х из второго уравнения приведенной формы модели. Приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, аналитически уступает структурной форме модели, т.к. в ней отсутствуют оценки взаимосвязи между эндогенными переменными.

Проблема идентификации

При переходу от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведённой и структурной формами модели.

Рассмотрим проблему идентификации для случая с двумя эндогенными переменными. Пусть структурная модель имеет вид:

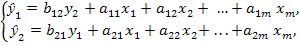
Где у_{1 и} у₂ – совместные зависимые переменные.

Из второго уравнения можно выразить 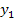следующей формулой:

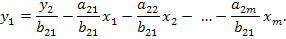
Тогда в системе имеем два уравнения для эндогенной переменной 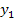с одним и тем же набором экзогенных переменных, но с разными коэффициентами при них:

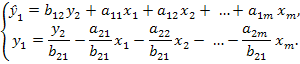
Наличие двух вариантов для расчёта структурных коэффициентов в одной и той же модели связано с неполной её идентификацией. Структурная модель в полном виде, состоящая в каждом уравнении системы из n эндогенных и m экзогенных переменных, содержит п ∙ (п — 1 + т) параметров. Так, при n=2 и m=3 полный вид структурной модели составит:

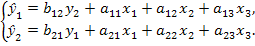(9.4)

Как видим, модель содержит восемь структурных коэффициентов, что соответствует выражению п ∙ (п — 1 + т).

Приведённая форма модели имеет вид:

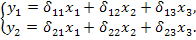
Действительно, она включает в себя шесть коэффициентов δ_ij.

На основе шести коэффициентов приведенной формы моде­ли требуется определить восемь структурных коэффициентов рассматриваемой структурной модели, что, естественно, не мо­жет привести к единственности решения. В полном виде струк­турная модель содержит большее число параметров, чем приве­денная форма модели. Соответственно п ∙ (п — 1 + т) параметров структурной модели не могут быть однозначно определены из пт параметров приведенной формы модели.

Для того чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некото­рые из структурных коэффициентов модели ввиду слабой взаи­мосвязи признаков с эндогенной переменной из левой части си­стемы равны нулю. Тем самым уменьшится число структурных коэффициентов модели. Так, если предположить, что в нашей модели а₁₃ = 0 и а₂₁ = 0, то структурная модель примет вид:

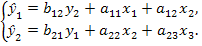(9.5)

В такой модели число структурных коэффициентов не пре­вышает число коэффициентов приведенной модели, которое равно шести. Уменьшение числа структурных коэффициентов модели возможно и другим путем: например, приравниванием некоторых коэффициентов друг к другу, т. е. путем предположе­ний, что их воздействие на формируемую эндогенную перемен­ную одинаково. На структурные коэффициенты могут наклады­ваться, например, ограничения вида b_ij + a_ij=0.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

• идентифицируемые;

• неидентифицируемые;

• сверхидентифицируемые.

Модель идентифицируема, если все структурные ее коэффици­енты определяются однозначно, единственным образом по коэф­фициентам приведенной формы модели, т. е. если число парамет­ров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты моде­ли оцениваются через параметры приведенной формы модели и модель идентифицируема. Рассмотренная выше структурная мо­дель (9.5) с двумя эндогенными и тремя экзогенными (предопределенными) переменными, содержащая шесть структурных ко­эффициентов, представляет собой идентифицируемую модель.

Модель неидентифицируема, если число приведенных коэф­фициентов меньше числа структурных коэффициентов, и в ре­зультате структурные коэффициенты не могут быть оценены че­рез коэффициенты приведенной формы модели. Структурная модель в полном виде (9.4), содержащая п эндогенных и т предо­пределенных переменных в каждом уравнении системы, всегда неидентифицируема.

Модель сверхидентифицируема, если число приведенных ко­эффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффици­ента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Так, если в структур­ной модели полного вида (9.4) предположить нулевые значения не только коэффициентов а₁₃ и а₂₁ (как в модели (9.5)), но и а₂₂ = 0, то система уравнений станет сверхидентифицируемой:

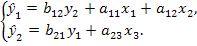(9.6)

В ней пять структурных коэффициентов не могут быть одно­значно определены из шести коэффициентов приведенной фор­мы модели. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему сов­местных уравнений, каждое из которых необходимо проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель счи­тается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Выполнение условия идентифицируемости модели проверя­ется для каждого уравнения системы. Для того чтобы уравнение было идентифицируемо, нужно, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутству­ющих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в j-м уравне­нии системы через Н, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в дан­ное уравнение, — через D, то условие идентифицируемости моде­ли может быть записано в виде следующего счетного правила:

D + I = Н — уравнение идентифицируемо;

D + 1 < Н— уравнение неидентифицируемо;

D + 1 > Н — уравнение сверхидентифицируемо.

Предположим, рассматривается следующая система одновре­менных уравнений:

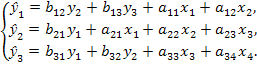(9.7)

Первое уравнение точно идентифицируемо, ибо в нем при­сутствуют три эндогенные переменные—у₁,у₂,у₃,т.е. H=3,и две экзогенные переменные — х₁ и х₂, число отсутствующих экзоген­ных переменных равно двум — x₃ и х₄, D =2. Тогда имеем равен­ство: D + 1 = Н, т. е. 2 + 1 = 3, что означает наличие идентифици­руемого уравнения.

Во втором уравнении системы Н = 2 (у₁ и у₂) и D = 1(х₄). Равенство D + 1 = Н, т.е. 1 + 1=2. Уравнение идентифицируемо.

В третьем уравнении системы Н=3 (у₁ , у₂, y₃), a D = 2 (х₁ и х₂). Следовательно, по счетному правилу D + 1 = Н, и это уравнение идентифицируемо. Таким образом, система (9.7) в целом иденти­фицируема.

Предположим, что в рассматриваемой модели а₂₁ = 0 и а₃₃ = 0. Тогда система примет вид:

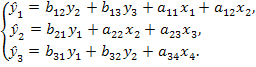(9.8)

Первое уравнение этой системы не изменилось. Система по-прежнему содержит три эндогенные и четыре экзогенные пе­ременные, поэтому для него D = 2 при H= 3, и оно, как и в предыдущей системе, идентифицируемо. Второе уравнение имеет Н= 2 и D = 2 (x₁ , x₄), так как 2+1 > 2. Данное уравнение сверхидентифицируемо. Также сверхидентифицируемым оказывается и третье уравнение системы, где Н= 3 (y_1, y₂, y₃) и D = 3 (х₁ х₂, х₃), т.е. счетное правило составляет неравенство: 3 + 1 > 3 или

D + 1 >Н. Модель в целом является сверхидентифицируемой.

Предположим, что последнее уравнение системы (9.8) с тре­мя эндогенными переменными имеет вид:

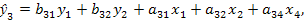
т. е. в отличие от предыдущего уравнения в него включены еше две экзогенные переменные, участвующие в системе, — х₁ и х₂. В этом случае уравнение становится неидентифицируемым, ибо при Н = 3, D = 1 (отсутствует только х₃) и D + 1 < Н, 1 + 1 < 3. Итак, несмотря на то, что первое уравнение идентифицируемо, второе сверхидентифицируемо, вся модель считается неидентифицируемой и не имеет статистического решения.

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Урав­нение идентифицируемо, если по отсутствующим в нем перемен­ным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определи­тель которой не равен нулю, а ранг матрицы не меньше, чем чис­ло эндогенных переменных в системе без одного.

Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других уравнениях, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но недостаточное условие иден­тификации.

Обратимся к следующей структурной модели:

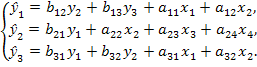(9.9)

Проверим каждое уравнение системы на необходимое и до­статочное условия идентификации. Для первого уравнения Н = 3 (у_{1 ,} у_2, у₃) и D = 2 (х₃ и х₄ отсутствуют), т. е. D + 1 = Н, необходи­мое условие идентификации выдержано, поэтому уравнение точ­но идентифицируемо. Для проверки на достаточное условие идентификации заполним следующую таблицу коэффициентов при отсутствующих в первом уравнении переменных, в которой определитель матрицы |A| коэффициентов равен нулю.

Матрица коэффициентов (1)

Уравнение	Переменные
x3	x4
	a23	a24

Следовательно, достаточное условие идентификации не выполняется и первое уравнение нельзя считать идентифици­руемым.

Для второго уравнения Н = 2 (у₁ и у₂), D = 1 (отсутствует х₁) счетное правило дает утвердительный ответ: уравнение иденти­фицируемо (D + 1 = Н).

Достаточное условие идентификации выполняется. Коэффи­циенты при отсутствующих во втором уравнении переменных со­ставят.

Матрица коэффициентов (2)

Уравнение	Переменные
y3	x1
	b13 – 1	a11 a31

Согласно таблице |A| ≠ 0, а ранг матрицы равен 2, что соот­ветствует следующему критерию: ранг матрицы коэффициентов должен быть не меньше числа эндогенных переменных в системе без одной. Итак, второе уравнение точно идентифицируемо.

Третье уравнение системы содержит Н = 3 и D = 2, т. е. по не­обходимому условию идентификации оно точно идентифицируе­мо (D + 1 = Н). Противоположный вывод имеем, проверив уравнение на достаточное условие идентификации. Составим таблицу коэффициентов при переменных, отсутствующих в тре­тьем уравнении, в которой |A| = 0.

Матрица коэффициентов (3)

Уравнение	Переменные
х 3	х4
	а23			а24

Из таблицы видно, что достаточное условие идентификации не выполняется. Уравнение неидентифицируемо. Следовательно, рассматриваемая в целом структурная модель, идентифицируе­мая по счетному правилу, не может считаться идентифицируемой исходя из достаточного условия идентификации.

В эконометрических моделях часто наряду с уравнениями, па­раметры которых должны быть статистически оценены, использу­ются балансовые тождества переменных, коэффициенты при ко­торых равны ±1. В этом случае хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при перемен­ных в тождестве известны, в проверке на идентификацию собст­венно структурных уравнений системы тождества участвуют.

Например, рассмотрим эконометрическую модель экономи­ки страны: _г

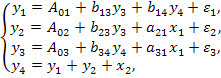
где у₁ — расходы на конечное потребление данного года;

А— свободный член уравнения;

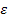— случайные ошибки;

у₂— валовые инвестиции в текущем году;

х₁— валовой доход предыдущего года;

y_з— расходы на заработную плату в текущем году;

у₄— валовой доход за текущий год;

х₂— государственные расходы текущего года.

В этой модели четыре эндогенные переменные у_1, у₂, у₃, y₄, причем переменная у₄ задана тождеством. Поэтому статистичес­кое решение практически необходимо только для первых трех уравнений системы, которые нужно проверить на идентифика­цию. Модель содержит две предопределенные переменные – эк­зогенную х₂ и лаговую х₁.

При практическом решении задачи на основе статистической информации за ряд лет или по совокупности регионов за один год в уравнениях для эндогенных переменных у₁ у₂, y₃ обычно содержится свободный член А₀₁, А₀₂, А₀₃, значение которого акку­мулирует влияние неучтенных в уравнении факторов и не влияет на определение идентифицируемости модели.

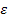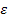Поскольку фактические данные об эндогенных переменных у₁, у₂, y₃ могут отличаться от теоретических, постулируемых мо­делью, принято в модель включать случайную составляющую для каждого уравнения системы, исключив тождества. Случайные составляющие (возмущения) обозначены через ₁, ₂ и 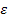₃,. Они не влияют на решение вопроса об идентификации модели.

В рассматриваемой эконометрической модели первое уравне­ние системы точно идентифицируемо, ибо H = 3 и D = 2, и вы­полняется необходимое условие идентификации (D + 1 = Н). Кроме того, выполняется и достаточное условие идентификации, т. е. ранг матрицы равен 3, а определитель ее не равен 0 : |A| =-a₃₁, что видно из следующей таблицы:

Уравнение	y2	x1	x2
	–1	а21
		– а31

Второе уравнение системы так же точно идентифицируемо: Н = 2 и D =1, т. е. счетное правило выполнено: D + 1 = Н, вы­полнено достаточное условие идентификации: ранг матрицы 3 и |A| = -b₃₄.

Уравнение	y1	y4	x2
	– 1	b14
		b34
		– 1

Третье уравнение системы также идентифицируемо: Н = 2, D=1,D+ 1 = Н; |A| ≠ 0, а ранг матрицы А = 3 и |A| = 1.

Уравнение	y1	y2	x2
	– 1
		– 1

Идентификация уравнений достаточно сложна и не ограни­чивается только вышеизложенным. На структурные коэффици­енты модели могут накладываться и другие ограничения, напри­мер, в производственной функции сумма эластичностей может быть равна по предположению 1. Могут накладываться ограниче­ния на дисперсии и ковариации остаточных величин.

3. Оценивание параметров структурной модели

Коэффициенты структурной модели могут быть оценены раз­ными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:

• косвенный метод наименьших квадратов (КМНК);

• двухшаговый метод наименьших квадратов (ДМНК);

• трехшаговый метод наименьших квадратов (ТМНК);

• метод максимального правдоподобия с полной информа­цией (ММП_f);

• метод максимального правдоподобия при ограниченной информации (ММП₅).

Косвенный и двухшаговый методы наименьших квадратов подробно описаны в литературе и рассматриваются как традици­онные методы оценки коэффициентов структурной модели. Эти методы достаточно легкореализуемы. Косвенный метод наи­меньших квадратов применяется для идентифицируемой систе­мы одновременных уравнений, а двухшаговый метод наимень­ших квадратов — для оценки коэффициентов сверхидентифицируемой модели. Перечисленные методы оценивания также используются для сверхидентифицируемых систем уравнений.

Приведем здесь косвенный метод наименьших квадратов. Косвенный метод наименьших квадра­тов используется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы:

• структурная модель преобразовывается в приведенную форму модели;

• для каждого уравнения приведенной формы модели обыч­ным МНК оцениваются приведенные коэффициенты (d_ij);

• коэффициенты приведенной формы модели трансформиру­ются в параметры структурной модели.

Рассмотрим применение КМНК для простейшей идентифи­цируемой эконометрической модели с двумя эндогенными и дву­мя экзогенными переменными:

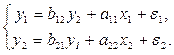
Пример. Пусть для построения данной модели мы распола­гаем некоторой информацией по пяти регионам (табл. 9.1).

Таблица 9.1

Условные данные по пяти регионам

Регион	у1	у2	х1	х2
Средние		6,2	2,4	3,4

При практических расчетах требуется, конечно, значительно больший объем информации, включающий достаточно большое число регионов.

Приведенная форма модели составит:

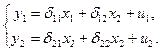
где и₁, и₂ – случайные ошибки приведенной формы модели.

Для каждого уравнения приведенной формы модели приме­няем традиционный МНК и определяем d-коэффициенты.

Чтобы упростить процедуру расчетов, можно работать с отклонениями от средних уровней, т. е. у = у – 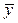и х = х – 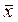. Тогда для первого уравнения приведенной формы модели система нормальных уравнений составит:

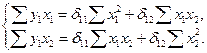
Применительно к рассматриваемому примеру, используя от­клонения от средних уровней, имеем:

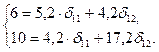
Решив данную систему, получим следующее первое уравне­ние приведенной формы модели:

у₁ = 0,852х₁ + 0,373х₂ + и₁.

Аналогично применяем МНК для второго уравнения приве­денной формы модели и получаем:

у₂ = d₂₁х₁ + d₂₂х₂ + и₂.

Система нормальных уравнений составит:

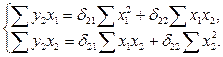
В соответствии с нашим примером имеем:

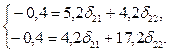
Откуда второе приведенное уравнение составит:

у₂ = – 0,0728х₁ – 0,00557х₂ + и₂.

Таким образом, приведенная форма модели имеет вид:

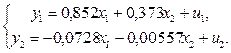
Переходим от приведенной к структурной форме модели, т. е. к системе уравнений

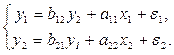
Для этой цели из первого уравнения приведенной формы мо­дели надо исключить х₂, выразив его из второго уравнения приве­денной формы и подставив в первое:

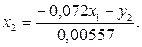
Тогда:

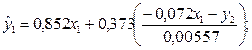
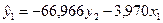– первое уравнение структурной мо­дели.

Для того чтобы найти второе уравнение структурной модели, обратимся вновь к приведенной форме модели. С этой целью из второго уравнения приведенной формы модели следует исклю­чить х₁, выразив его через первое уравнение и подставив во второе:

Итак, структурная форма модели имеет вид:

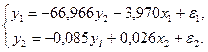
Оценка значимости модели дается через F-критерий и R² для каждого уравнения в отдельности. В рассматриваемом примере хороших результатов достичь не удалось: ввиду малого числа наблюдений значения F-критерия Фишера несущественны (при уровне значимости 0,05 F-табличное значение равно 19, а фактическое F = 7 для первого уравнения).

Контрольные вопросы:

1. Какие системы уравнений используются в эконометрике?

2. Какие переменные в системе одновременных уравнений называют экзогенными, а какие – эндогенными?

3. Какой вид имеет структурная форма модели?

4. Какой вид приведенной формы модели?

5. Как связаны между собой структурная и приведенная формы моделей?

6. В чем состоят проблемы идентификации модели?

7. Какие модели называют идентифицируемыми, неидентифицируемыми, сверхидентифицируемыми?

8. Каковы необходимые и достаточные условия идентификации?

9. В чем суть косвенного метода наименьших квадратов?

Используемая литература

1. Кремер, Н.Ш. Эконометрика: учебник / Н.Ш. Кремер, Б. А. Путко. – М.: ЮНИТИ-ДАНА, 2010.

2. Елисеева, И.И. Эконометрика: учеб. пособие / под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2007.

3. Елисеева, И.И. Практикум по эконометрике / под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2007.

4. Магнус, Я.Р. Эконометрика. Начальный курс / Я.Р. Магнус,П.К. Катышев, А.А. Пересецкий. – М.: Дело, 2000.

5. Бородич, С.А. Эконометрика /С.А. Бородич.– Минск: Новое знание, 2004.

6. Красс, М.С. Математика для экономистов: учеб. пособие. / М.С. Красс, Б.П. Чупрынов. СПб.: Питер, 2009.

7. Мхитарян, В.С. Эконометрика: учебник / В.С. Мхитарян, М.Ю. Архипова, В.А. Балаш и др. – М.: Проспект, 2009 .

8. Айвазян, С.А. Прикладная статистика и основы эконометрики: учебник / С. А. Айвазян, В.С. Мхитарян. – М.: ЮНИТИ, 2002.

Конспекты лекций

по дисциплине

«Эконометрика»

Автор

Цвиль Мария Михайловна

Издано в авторской редакции