Модели с распределенными лагами

Модели с распределенными лагами бывают двух типов:

· с конечным числом лагов:

;

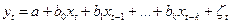· с бесконечным числом лагов:

.

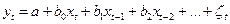Практическое применение чаще всего имеют модели с конечным числом лагов, т.е. модели, в которых число лагов экспериментально определено.

Предположим рассматривается модель, в которой 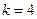, т.е. 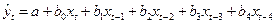. Данная модель означает, что изменение во времени 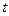объясняющей переменной 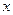будет влиять на значения результативного признака 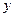в течении 4 следующих моментов времени.

Коэффициент 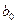называют краткосрочным мультипликатором, так как он характеризует среднее изменение результата 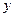при изменении 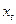на 1 единицу своего измерения в фиксированный момент времени .

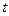В момент времени 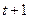воздействие объясняющей переменной 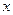на результат 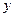составит 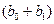единиц, а в момент времени 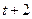общее изменение 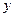составит 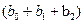единиц.

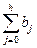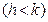Любую сумму коэффициентов , где называют промежуточным мультипликатором, а сумму всех коэффициентов регрессии 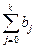- долгосрочным мультипликатором, который характеризует общее изменение 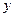через 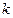интервалов времени под воздействием изменения 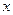в момент 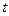на 1 единицу.

При 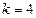долгосрочный мультипликатор составит 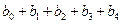. Он характеризует общее среднее изменение 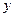через 4 временных интервала при увеличении 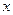в момент времени 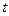на 1 единицу, а промежуточные мультипликаторы:

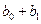- изменение 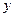в момент времени ;

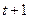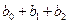- изменение 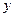в момент времени ;

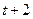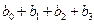- изменение 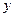в момент времени .

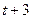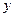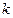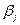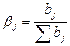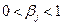Если все коэффициенты регрессии имеют одинаковые знаки, т.е. характеризуются однонаправленным изменением в исследуемые моментов времени, то можно определять относительные коэффициенты модели , т.е. , где , а 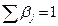. Иными словами, 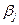характеризует долю общего изменения 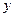в момент времени .

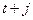Модель с конечным числом лагов при правильной ее спецификации может быть оценена обычным МНК. В этом случае в уравнении:

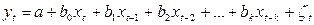
переменные 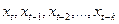рассматриваются как объясняющие переменные обычной множественной регрессии.

Вместе с тем применение МНК к моделям с конечным числом лагов может быть реально затруднено ввиду следующих причин:

1) при наличии тенденции переменные 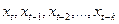тесно связаны между собой, что вызывает мультиколлинеарность факторов, которая может привести к неинтерпретируемым знакам у коэффициентов регрессии и к снижению их точности;

2) возможна автокорреляция остатков, так как МНК применяется к временным рядам с тенденцией.

Поэтому нередко для оценки параметров модели с распределенным конечным числом лагов используются специальные методы преобразования, как и для модели с бесконечным числом лагов. Разработаны разные методы оценивания параметров моделей с распределенными лагами, которые учитывают характер распределения коэффициентов регрессии при лаговых объясняющих переменных. Иными словами, методы оценивания параметров модели с распределенными лагами основаны на изучении структуры лага. Так, предполагая полиномиальное распределение лаговых коэффициентов, используется метод Алмон, а при гипотезе геометрической прогрессии для лаговых коэффициентов применяется преобразование Койка.

Модели авторегрессии

Достаточно распространены авторегрессионные модели вида:

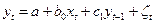. (8.1)

Для модели (8.1), как и в модели с распределенными лагами, параметр 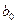характеризует краткосрочное изменение 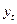под воздействием 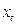на 1 единицу. Параметр 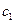по существу представляет собой величину 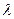из преобразования Койка, т.е. 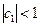и показывает коэффициент снижения лаговых коэффициентов при увеличении значения лага в соответствии с концепцией их геометрического убывания. Следовательно, к моменту времени 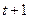результат 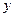изменится дополнительно на 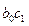единиц, а к моменту времени 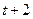дополнительное изменение 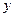составит 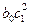единиц, к моменту времени 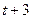- 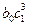и т.д. Соответственно долгосрочный мультипликатор окажется равным:

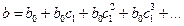(в предположении бесконечного числа лагов).

Учитывая геометрическую прогрессию лаговых коэффициентов,

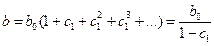- долгосрочный мультипликатор изменения .

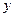В силу того, что в авторегрессии в правой части содержатся лаговые эндогенные переменные, принято считать, что оценка параметров традиционным МНК дает неудовлетворительные результаты.

Предположим, что рассматривается модель авторегрессии вида (8.1) .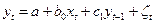

Применение для оценивания параметров уравнения (8.1) традиционного МНК возможно, если выполняется предпосылка МНК относительно отсутствия автокорреляции остатков. Между тем при наличии в правой части лаговой зависимой переменной может иметь место автокорреляция остатков. Кроме того, может иметь место и зависимость объясняющей переменной 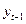с остатками 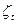, т.е. нарушается предпосылка о гомоскедастичности остатков. В силу этого классический метод наименьших квадратов в малых выборок даст смещенные оценки параметров.

Одним из возможных методов оценивания параметров модели (8.1) является метод инструментальных переменных. Суть метода состоит в том, что вместо лаговой зависимой переменной 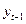, для которой нарушается предпосылка МНК, используется другая переменная, называемая инструментальной. При этом инструментальная переменная должна обладать двумя свойствами:

· она должна быть тесно коррелированна с лаговой переменной ;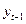

· она не должна коррелировать с остатками 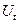(случайными ошибками).

Иными словами, от модели авторегрессии (8.1) необходимо перейти к модели вида:

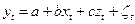. (8.2)

Результаты регрессии по модели (8.2), естественно, зависят от того, насколько удачно подобрана инструментальная переменная. В качестве инструментальной переменной можно, например, взять оценку 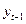, т.е. 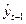, полученную по регрессии 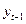от .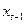

Поскольку в модели (8.1) предполагается наличие зависимости 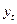от 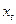, то можно предположить, что также имеет место зависимость 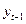от 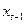, т.е. найдем регрессию

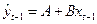. . (8.3)

Используя для оценки параметров уравнения (8.3) обычный МНК, что возможно ввиду отсутствия в правой части модели лаговой зависимой переменной, найдем теоретические значения 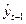, которые и будут рассматриваться как значения инструментальной переменной 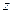в модели (8.2). Далее вновь применяем МНК уже к модели (8.2), т.е. по существу оценка параметров модели авторегрессии (8.1) будет найдена исходя из модели вида

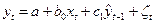. (8.4)

Если вместо оценки 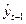подставить выражение (8.3), то получим следующую модель:

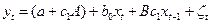. (8.5)

Она представляет собой модель с распределенным лагом, оценка параметров которой может быть дана МНК.

Таким образом, используя в качестве инструментальной переменной оценки 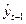, исходя из регрессии 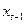(8.3), модель авторегрессии (8.1) заменяется на модель с распределенным лагом (8.5).