Модели регрессии с фиктивными переменными сдвига

Рассмотрим в качестве формы уравнения регрессии линейную функцию. Для простоты возьмем в качестве факторов одну количественную переменную х₁ и одну фиктивную переменную z₁₁:

y = a + b₁x₁ + c₁₁z₁₁ + e. (6.3)

Из этого уравнения следует, что при z₁₁ = 1 результат (у) равен

y = (a + c₁₁)+ b₁x₁ + e, (6.4)

а при z₁₁ = 0 результат (у) равен:

y = a + b₁x₁ + e. (6.5)

Сравнивая два полученных уравнения (6.4) и (6.5), видим, что они различаются величиной свободного члена. То есть для одного уровня неколичественной переменной уровень результата всегда в среднем будет на с₁₁ единиц выше и ниже, чем для другого.

Графически эта ситуация соответствует двум параллельным прямым. Отметим, что коэффициент b₁ при количественном факторе остается неизменным. То есть изменение фактора x₁ оказывает одинаковое влияние на результат при разных значениях неколичественной переменной.

Так как изменение значения фиктивной переменной в модели (6.3) приводит к изменению значения результата на некую среднюю величину, не зависящую от значений количественного фактора, такую переменную еще называют фиктивной переменной сдвига. Изменение ее значения приводит к переходу от одной параллельной прямой к другой.

Модели регрессии с фиктивными переменными наклона

Рассмотрим другую ситуацию: коэффициент регрессии при количественном факторе зависит от значения фиктивной переменной. То есть можно записать:

если z = 0; (6.6)

если z = 1; (6.7)

b₁₁ ¹ b₁₂.

В таком случае говорят, что имеют место структурные изменения в исследуемой зависимости. Для их учета в уравнении регрессии фиктивную переменную вводят как сомножитель при количественной переменной:

(6.8)

Так как параметр d объединяет две переменные – х₁ и z₁₁, он имеет тройной индекс – d₁₁₁.

Действительно, если рассмотреть это уравнение для z₁₁ = 1 и для z₁₁ = 0, получим соответственно

z₁₁ = 0

z₁₁ = 1

Следовательно, коэффициент b₁₂ из модели (6.7) будет равен (b₁₁ + d₁₁₁).

Графически модель можно представить в виде двух прямых с разным углом наклона, отражающих зависимость результата от количественного фактора при разных значениях фиктивной переменной. Так как речь идет о фиктивной переменной, включение которой позволяет изменить угол наклона прямой, такую переменную называют фиктивной переменной наклона.

Соответственно параметр b₁ интерпретируется как сила влияния количественного фактора при одном значении неколичественной переменной (для которой z₁₁ = 0), а параметр d₁₁₁ – как среднее изменение силы влияния количественного фактора при переходе от одного значения неколичественной переменной к другому (при переходе от z₁₁ = 0 к z₁₁ = 1).

Модели типа (6.8) используются при исследовании зависимости объема потребления Y некоторого продукта от дохода потребителя X, когда качественные признаки (например, уровень доходности домашнего хозяйства) на параметр b₁ при X, интерпретируемый как

«склонность к потреблению».

Критерий Г. Чоу

В практике эконометриста нередки случаи, когда имеются две выборки пар значений зависимой и объясняющих переменных . Например, одна выборка пар значений переменных объемом получена при одних условиях, а другая, объемом , –при несколько измененных условиях. Необходимо выяснить, действительно ли две выборки однородны в регрессионном смысле? Другими словами, можно ли объединить две выборки в одну и рассматривать единую модель регрессии 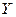по ?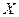

При достаточных объемах выборок можно было, например, построить интервальные оценки параметров регрессии по каждой из выборок и в случае пересечения соответствующих доверительных интервалов сделать вывод о единой модели регрессии. Возможны и другие подходы.

В случае, если объем хотя бы одной из выборок незначителен, то возможности такого подхода резко сужаются из-за невозможности построения сколько-нибудь надежных оценок.

В критерии (тесте) Г. Чоу эти трудности в существенной степени преодолеваются. По каждой выборке строятся две линейные регрессионные модели:

, ;

, .

Проверяется нулевая гипотеза : , где ‑ векторы параметров двух моделей; – их случайные возмущения.

Если нулевая гипотеза верна, то две регрессионные модели можно объединить в одну объема :

, .

Согласно критерию Г. Чоу нулевая гипотеза отвергается на уровне значимости 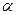, если статистика

, (6.9)

где , , ‑остаточные суммы квадратов соответственно для объединенной, первой и второй выборок; .

Критерий Г. Чоу может быть использован при построении регрессионных моделей при воздействии качественных признаков, когда имеется возможность разделения совокупности наблюдений по степени воздействия этого фактора на отдельные группы и требуется установить возможность использования единой модели регрессии.

Контрольные вопросы:

1. Можно ли учесть в уравнении регрессии неколичественные факто­ры? Каким образом?

2. Дайте определение фиктивной переменной.

3. Сколько фиктивных переменных нужно ввести, если имеются два неколичественных фактора, причем один из них имеет три возможных значения, а другой – два?

4. Как интерпретируется коэффициент регрессии при фиктивной пе­ременной сдвига?

5. Как интерпретируется коэффициент регрессии при фиктивной пе­ременной наклона?

6. Каков общий вид модели регрессии с одной количественной и од­ной фиктивной переменной?

7. Назовите достоинства и недостатки моделей с фиктивными пере­менными.

8. Пусть имеется уравнение регрессии с одним количественным и одним неколичественным фактором, выраженным тремя фиктивными пе­ременными. Сколько возможных значений у неколичественного фактора? Как на основе заданного уравнения регрессии найти уравнения парной регрессии, содержащие только количественный фактор? Сколько будет таких уравнений и почему?

9. Какова область применения теста Чоу?

10. Какие показатели сравниваются между собой по тесту Чоу? Какой статистический критерий в этом случае используется?

11. Опишите методику применения теста Чоу.