Тема 6. линейные регрессионные модели

С ПЕРЕМЕННОЙ СТРУКТУРОЙ.

ФИКТИВНЫЕ ПЕРЕМЕННЫЕ

План лекции

1. Фиктивные переменные.

2. Модели регрессии с фиктивными переменными сдвига.

3. Модели регрессии с фиктивными переменными наклона.

4. Критерий Г. Чоу.

Введение

До сих пор мы рассматривали регрессионную модель, в которой в качестве объясняющих переменных (регрессоров) выступали количественные переменные (производительность труда, себестоимость продукции, доход и т. п.). Однако на практике достаточно часто возникает необходимость исследования влияния качественных признаков, имеющих два или несколько уровней (градаций). К числу таких признаков можно отнести: пол (мужской, женский), образование (начальное, среднее, высшее), фактор сезонности (зима, весна, лето, осень) и т. п.

Качественные признаки могут существенно влиять на структуру линейных связей между переменными и приводить к скачкообразному изменению параметров регрессионной модели. В этом случае говорят об исследовании регрессионных моделей с переменной структурой или построении регрессионных моделей по неоднородным данным.

Фиктивные переменные

Например, нам надо изучить зависимость размера заработной платы 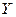работников не только от количественных факторов 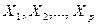,но и от качественного признака 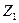(например, фактора «пол работника»).

В принципе можно было получить оценки регрессионной модели

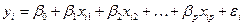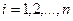, (6.1)

для каждого уровня качественного признака (т. е. выборочное уравнение регрессии отдельно для работников-мужчин и отдельно – для женщин), а затем изучать различия между ними.

Но есть и другой подход, позволяющий оценивать влияние значений количественных переменных и уровней качественных признаков с помощью одного уравнения регрессии. Этот подход связан с введением так называемых фиктивных (манекенных) переменных, или манекенов (dummy variables).

В качестве фиктивных переменных обычно используются бинарные, булевы переменные, которые принимают всего два значения: «0» или «1» (например, значение такой переменной 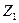по фактору «пол»: 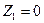для работников-женщин и 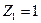‑для мужчин).

В этом случае первоначальная регрессионная модель (6.1) заработной платы изменится и примет вид:

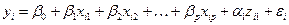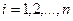, , (6.2)

где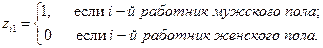

Таким образом, принимая модель (6.2), мы считаем, что средняя заработная плата у мужчин на 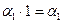выше, чем у женщин, при неизменных значениях других параметров модели. А проверяя гипотезу : 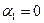, мы можем установить существенность влияния фактора «пол» на размер заработной платы работника.

Следует отметить, что качественное различие можно формализовать с помощью любой переменной, принимающей два разных значения, не обязательно «0» или «1». Однако в эконометрической практике почти всегда используются фиктивные переменные типа «0 ‑ 1», так как при этом интерпретация полученных результатов выглядит наиболее просто. Если рассматриваемый качественный признак имеет несколько 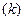уровней (градаций), то в принципе можно было ввести в регрессионную модель дискретную переменную, принимающую такое же количество значений (например, при исследовании зависимости заработной платы 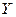от уровня образования 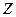можно рассматривать 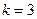значения: 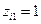при наличии начального образования, 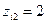– среднего и 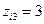при наличии высшего образования). Однако обычно так не поступают из-за трудности содержательной интерпретации соответствующих коэффициентов регрессии, а вводят 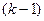бинарных переменных.

При включении в уравнение регрессии фиктивных переменных возникает вопрос о характере влияния количественных факторов на результат при различных значениях неколичественного фактора. Далее будут рассмотрены различные варианты моделей регрессии с фиктивной переменной.