Суть гетероскедастичности, ее последствия
При практическом проведении регрессионного анализа с помощью МНК следует обратить серьезное внимание на проблемы, связанные с выполнимостью свойств случайных отклонений моделей. Как отмечалось ранее, свойства оценок коэффициентов регрессии напрямую зависят от свойств случайного члена в уравнении регрессии. Для получения качественных оценок необходимо следить за выполнимостью предпосылок МНК (условий Гаусса - Маркова), так как при их нарушении МНК может давать оценки с плохими статистическими свойствами.
На практике гетероскедастичность не так уж и редка. Зачастую есть основания считать, что вероятностные распределения случайных отклонений  при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми – при других, но это означает, что априорная вероятность этого велика. Поэтому важно понимать суть этого явления и его последствия.
при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми – при других, но это означает, что априорная вероятность этого велика. Поэтому важно понимать суть этого явления и его последствия.
На рис. 5.1 приведены два примера линейной регрессии – зависимости потребления С от дохода I:  .
.

Рис. 5. 1
В обоих случаях с ростом дохода растет среднее значение потребления. Но если на рис.5.1, а дисперсия потребления остается одной и той же для различных уровней дохода, то на рис.5.1,б при аналогичной зависимости среднего потребления от дохода дисперсия потребления не остается постоянной, а увеличивается с ростом дохода. Фактически это означает, что во втором случае субъекты с большим доходом в среднем потребляют больше, чем субъекты с меньшим доходом, и, кроме того, разброс в их потреблении более существенен для большего уровня дохода. Люди с большим доходом имеют больший простор для его распределения. Реалистичность данной ситуации не вызывает сомнений. Разброс значений потребления вызывает разброс точек наблюдения относительно линии регрессии, что и определяет дисперсию случайных отклонений. При гомоскедастичности дисперсии  постоянны, а при гетероскедастичности дисперсии
постоянны, а при гетероскедастичности дисперсии  изменяются (в нашем случае увеличиваются).
изменяются (в нашем случае увеличиваются).
При гетероскедастичности последствия применения МНК будут следующими:
1. Оценки коэффициентов по-прежнему останутся несмещенными и линейными.
2. Оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.
3. Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что не объясненная уравнением регрессии дисперсия  (m – число объясняющих переменных), которая используется при вычислении оценок дисперсий всех коэффициентов, не является более несмещенной.
(m – число объясняющих переменных), которая используется при вычислении оценок дисперсий всех коэффициентов, не является более несмещенной.
4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих 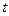 и
и  – статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, стандартные ошибки коэффициентов будут занижены, а следовательно,
– статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, стандартные ошибки коэффициентов будут занижены, а следовательно, 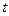 - статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющихся.
- статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющихся.
На рис. 5.2 видно, что для каждого конкретного значения 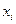 СВ Х переменная Y принимает значение
СВ Х переменная Y принимает значение 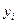 из некоторого множества, имеющего свое распределение, отличное одно от другого в силу непостоянства дисперсий (сравните распределения для значений
из некоторого множества, имеющего свое распределение, отличное одно от другого в силу непостоянства дисперсий (сравните распределения для значений  и
и  ).
).

Рис. 5. 2
По МНК минимизируется сумма квадратов отклонений
 .
.
Но в этом случае каждое конкретное значение  в данной сумме имеет одинаковый «вес» вне зависимости от того, получено оно из распределения с маленькой дисперсией (например,
в данной сумме имеет одинаковый «вес» вне зависимости от того, получено оно из распределения с маленькой дисперсией (например,  ) или с большой (например,
) или с большой (например,  ). но это противоречит логике, так как точка, полученная из распределения с меньшей дисперсией, более точно определяет направление линии регрессии. Поэтому она должна иметь больший «вес», чем точка из распределения с большей дисперсией. Следовательно, методы оценивания, учитывающие «веса» точек наблюдений, позволяют получать более точные (эффективные) оценки. Учет «весов» точек характерен, например, для метода взвешенных наименьших квадратов, рассмотренного ниже.
). но это противоречит логике, так как точка, полученная из распределения с меньшей дисперсией, более точно определяет направление линии регрессии. Поэтому она должна иметь больший «вес», чем точка из распределения с большей дисперсией. Следовательно, методы оценивания, учитывающие «веса» точек наблюдений, позволяют получать более точные (эффективные) оценки. Учет «весов» точек характерен, например, для метода взвешенных наименьших квадратов, рассмотренного ниже.
