Отбор факторов в случае линейной множественной регрессии

Если факторы-аргументы не являются случайными величинами, то коэффициенты корреляции не могут быть использованы при построении уравнения регрессии, так как они не могут быть интерпретированы как показатели тесноты связи.

Существенность вводимых факторов в случае линейной множественной регрессии может быть проверена одновременно с существенностью коэффициентов регрессии.

Для проверки существенности вычисляется отношение

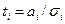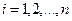, (4.7)

где 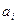– коэффициент множественной регрессии; 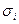– среднее квадратическое отклонение этого коэффициента.

Если t_i<t_табл, взятого по таблицам t-распределения Стьюдента, то с заданной вероятностью не отвергается гипотеза, что соответствующий коэффициент регрессии 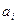в генеральной совокупности (который не известен и который нужно оценить по данным выборки) равняется нулю. При этом i-ый фактор в таком случае признается несущественным для построенного уравнения регрессии.

При проведении исследования может оказаться, что вычисленные значения t для нескольких факторов не превышают t_табл. В этом случае несущественные факторы из уравнения регрессии исключаются поочередно, начиная с наименьшего по абсолютной величине t. Фактор соответствующий минимальному значению t, из уравнения регрессии исключается, и заново решается система нормальных уравнений. Затем вновь вычисляются значения t для всех оставшихся в уравнении коэффициентов, определяется минимальное значение t, которое сопоставляется с t_табл. Если окажется, что t_min<t_табл, то фактор, имеющий t_min, исключается.

Процесс исключения коэффициентов повторяется до тех пор, пока не будет выполняться соотношение t_min≥t_табл. В этом случае все оставшиеся в уравнении факторы существенны.

Проводить исключение из уравнения регрессии одновременно несколько факторов, имеющих t<t_табл, нецелесообразно, так как после исключения одного несущественного фактора коэффициенты регрессии других факторов меняются и несущественные факторы после пересчета могут оказаться существенными.

Аналогичный подход осуществляется и при наличии корреляционной зависимости, но на последней стадии отбора существенных факторов. Проверка значимости уравнения регрессии осуществляется по критерию Фишера

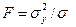(4.8)

с числом степеней свободы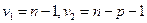

где

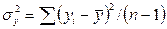(4.9)

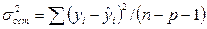(4.10)

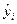значения у, полученные по данным наблюдений; у_i – расчетные значения у, полученные для соответствующих значений .

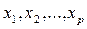Полученное значение F сравнивается с F_табл при выбранном уровне значимости. Если окажется F>F_табл, то гипотеза о том, что не имеют существенного влияния на у , отвергается.

Если F>F_табл, то следует ввести некоторые другие факторы, влияющие на показатель у, или перейти к построению нелинейной множественной регрессии.

При построении регрессионного уравнения весьма существенную информацию о модели может дать рассмотрение остатков .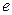

Контрольные вопросы:

11. Какие требования предъявляются к объему наблюдений, необходимому для построения уравнения регрессии?

12. Какие требования предъявляются к факторам, включаемым в уравнение регрессии?

13. Что такое мультиколлинеарность факторов и как ее выявить?

14. Как вычисляются парные коэффициенты корреляции, частные коэффициенты корреляции?

15. Какова формула для вычисления коэффициента множественной детерминации?

16. Какой критерий используется для оценки значимости параметров уравнения регрессии?

Что понимают под значимостью модели регрессии в целом?