Методом наименьших квадратов

Для оценки вектора неизвестных параметров 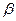применим метод наименьших квадратов. Так как произведение транспонированной матрицы 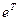на саму матрицу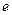

,

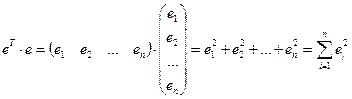то условие минимизации остаточной суммы квадратов запишется в виде:

.

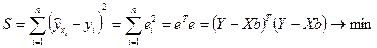Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, т.е. 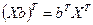, после раскрытия скобок получим:

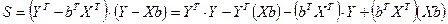
Произведение 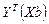есть матрица размерности 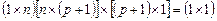, т.е. величина скалярная, следовательно, оно не меняется при транспонировании, т.е.

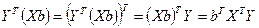
Поэтому условие минимизации примет вид:

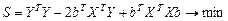
На основании необходимого условия экстремума функции нескольких переменных S 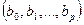, необходимо приравнять к нулю частные производные по этим переменным 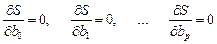или в матричной форме – вектор частных производных 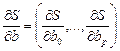должен быть ноль-вектором 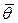, т.е. .

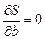Известно (из алгебры матриц) для векторов: , , .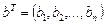

.

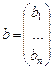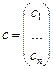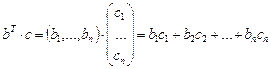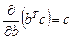
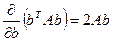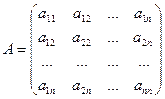, где – симметрическая матрица, в которой элементы, расположенные симметрично главной диагонали, равны.

Поэтому, полагая 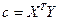, а матрица 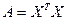(она является симметрической), найдем

,

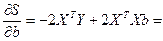
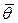откуда получаем систему нормальных уравнений в матричной форме для определения вектора :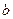

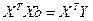. (3.4)

Найдем матрицы, входящие в это уравнение.

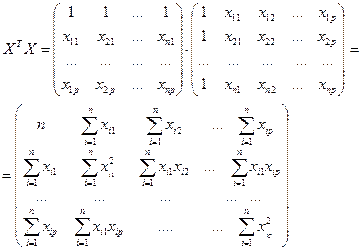
Матрица 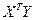есть вектор произведений n наблюдений объясняющих и зависимой переменных:

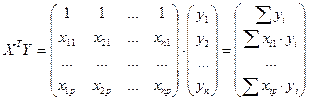
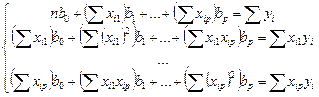(3.5)

При 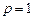получим систему нормальных уравнений:

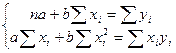
Для решения системы (3.5) или матричного уравнения (3.4) нужна еще одна предпосылка: 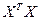- невырожденная матрица, т.е. 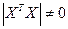. Тогда решение имеет вид:

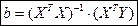. (3.6)

В модели (3.2) 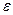- случайный вектор, Х – неслучайная матрица.

Предпосылки для множественного регрессионного анализа.

Модель

, .

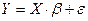
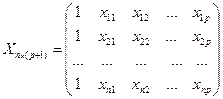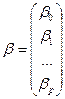1. 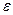– случайный вектор, 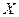- неслучайная матрица;

2. ;

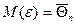3. ;

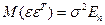4. 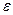- нормально распределенный случайный вектор, т.е. ;

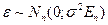5. .

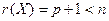Модель, удовлетворяющая указанным предпосылкам называется классической нормальной линейной моделью множественной регрессии. Если п.4 не выполняется, то модель называется просто классической линейной моделью множественной регрессии.

Теорема Гаусса-Маркова.

Если предпосылки (1)-(5) множественного регрессионного анализа выполняются, то оценка 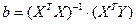метода наименьших квадратов является эффективной, т.е. обладает наименьшей дисперсией в классе линейных несмещенных оценок.

Зная вектор b, выборочное уравнение множественной регрессии имеет вид:

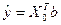(3.6)

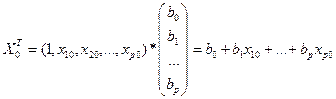
Пример.

Имеются данные о сменной добыче угля на одного рабочего 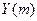, мощности пласта 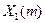и уровня механизации работ 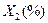, характеризующие процесс добычи угля в 10 шахтах.

Предполагая, что между переменными 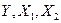существует линейная корреляционная зависимость, найти уравнение регрессии 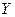по .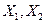

Решение этого примера подробно изложено в учебнике [1] с.88.

В результате вычислений имеем уравнение множественной регрессии вида:

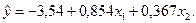
Оно показывает, что при увеличении только мощности пласта Х₁ (при неизменном Х₂) на 1 м добыча угля на одного рабочего У увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ Х₂ (при неизменном Х₁) – в среднем на 0,367 т.

i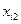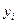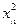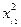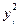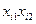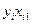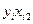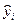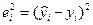
										5,13	0,016
										8,79	1,464
										9,64	1,127
										5,98	1,038
										5,86	0,741
										6,23	0,052
										6,35	1,121
										5,61	1,377
										5,13	0,762
										9,28	1,631
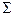										-	6,329