Закачка фильтрующейся жидкости

Если жидкость, закачиваемая в пласт для распространения трещины, фильтрующаяся, то распространение трещин при гидравлическом разрыве пласта получается иным. Теперь уже нельзя полагать, что жидкость не может дойти до конца трещины, поэтому давление жидкости в конце трещины совсем не обязательно должно быть равно нулю.

Самое же главное в механизме образования трещин при помощи фильтрующейся жидкости заключается в том, что деформация пород при этом происходит под действием на породы поля градиентов давления фильтрующейся жидкости. Кроме того, более сложными являются гидравлические зависимости в самой трещине, так как жидкость не только движется по трещине, но и постепенно отфильтровывается в пласт. Однако в некоторых случаях можно существенно упростить задачу об образовании трещин. Рассмотрим, например, образование трещин в пористых и проницаемых породах при помощи фильтрующейся жидкости, вязкость которой намного превышает вязкость пластовой жидкости. Кроме того, примем, что вязкая жидкость профильтровывается в пласт на сравнительно небольшое расстояние от поверхностей трещины, как это показано на рисунке 8.7. Тогда можно полагать, что практически трещина образуется под действием усилия, приложенного к поверхности трещины, однако давление жидкости, или теперь уже перепад давления жидкости, не равно нулю в конце трещины.

Рисунок 8.7 – Образование трещины путем закачки в нее фильтрующейся жидкости

Если размеры области, занятой профильтровавшейся в пласт жидкостью в соответствии с рисунком 8.7 малы, то, рассматривая совместно задачу теории упругости и фильтрации, получаем следующие выражения для определения полудлины трещины 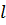и ее максимальной ширины :

(8.19)

В аналогичном случае образования горизонтальной трещины при помощи фильтрующейся жидкости используется решение задачи теории упругости о действии давления на поверхности трещины распределенного по параболическому закону. Считая, что вязкая жидкость отфильтровывается от горизонтальной трещины симметрично и достигает радиуса 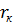, получаем зависимость между объемом закачанной жидкости , радиусом трещины R и другими параметрами в следующей форме:

(8.20)

Эта зависимость представлена на рисунке 8.8. В приведенной выше постановке задач об образовании трещин при помощи фильтрующейся жидкости фактически не принималось во внимание действие на пласт градиентов давления фильтрующейся жидкости, так как считалось, что размер области, занятой профильтровавшейся в пласт жидкостью, мал по сравнению с размерами трещин. Покажем на простом примере, в каких случаях можно так считать. Пусть имеем два образца пористой среды цилиндрической формы, составленные вместе соответственно рисунку 8.9 и сжатые с торцов давлением 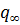, имитирующим боковое горное давление. Допустим также, что каким-то образом в оба образца в место их соприкосновения (в плоскость ) подается жидкость и в пределах области, занятой профильтровавшейся , происходит установившаяся фильтрация и, следовательно, на пористую среду обоих образцов действуют градиенты давления фильтрующейся жидкости, вызывая в пористой среде распределение давления и сжимающего напряжения, показанное на рисунке 8.9.

Нетрудно показать, что полное смещение (изменение расстояния между торцами) у одного из образцов, если его сжать давлением, равным 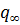, будет . Когда же на образец действует давление фильтрующейся жидкости в соответствии с эпюрой, изображенной на рисунке 8.9, смещение в плоскости будет . Разъединение образцов в плоскости (раскрытие «трещины») наступит, когда . Тогда будет

(8.21)

Рисунок 8.8 – Зависимость параметра от параметра

Рисунок 8.9 – Образование щели в пористой среде под воздействием фильтрующейся жидкости:

1 – образец пористой среды; 2 – направление фильтрации жидкости

Из этого простого примера видно, что при , а при больших для начала раскрытия трещины потребуется . Изложенная выше схема образования трещин в пластах при помощи фильтрующейся жидкости относится к случаю .