Горизонтальные трещины с параболическим распределением давления
В аналогичном случае, когда нагрузка на внутреннюю поверхность осесимметричной горизонтальной трещины распределена по параболическому закону, а все остальные условия — те же, что и в предыдущем случае, имеем следующее соотношение, отражающее условие конечности напряжений в конце трещины:
 | (8.10) |
где  - давление в точке
- давление в точке  ,
,
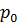 – давление в точке
– давление в точке  .
.
Ширина трещины  определяется формулой
определяется формулой
 | (8.11) |
На рисунке 8.5 показана форма трещины согласно зависимости (8.11), где  - максимальная ширина трещины при
- максимальная ширина трещины при 

Рисунок 8.5 – Зависимость  от
от 
Приведенные выше решения позволяют хорошо описать процесс распространения трещин при гидравлическом разрыве пластов. Однако, помимо деформации пород, при описании гидравлического разрыва пластов необходимо учитывать также гидравлические закономерности.
Закачка нефильтрующейся жидкости
Образование горизонтальной трещины в результате закачки нефильтрующейся жидкости
Рассмотрим, например, процесс распространения горизонтальной трещины (рисунок 8.6), образующейся в результате закачки в нее нефильтрующейся жидкости или, что то же, когда горные породы, в которых развивается трещина, являются непористыми и непроницаемыми. По стволу скважины 1, показанной на рис. 8.6, закачивается жидкость в трещину 2, в результате чего радиус горизонтальной трещины  увеличивается, а также изменяются ширина трещины
увеличивается, а также изменяются ширина трещины  и давление жидкости в трещине
и давление жидкости в трещине 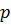 . Горные породы сжаты сверху горным давлением
. Горные породы сжаты сверху горным давлением  . Поскольку жидкость является абсолютно нефильтрующейся, следует полагать, что она не может дойти до самого конца трещины, где ширина трещины равна нулю, а доходит лишь до радиуса
. Поскольку жидкость является абсолютно нефильтрующейся, следует полагать, что она не может дойти до самого конца трещины, где ширина трещины равна нулю, а доходит лишь до радиуса  .
.
Обобщая известный закон движения жидкости в щели применительно к трещине переменной ширины  и радиальному движению жидкости, получаем (рисунок 8.6)
и радиальному движению жидкости, получаем (рисунок 8.6)
 | (8.12) |
Отсюда имеем следующее уравнение для расчета изменения давления жидкости вдоль горизонтальной трещины
 | (8.13) |
где  - расход закачиваемой в трещину жидкости.
- расход закачиваемой в трещину жидкости.

Рисунок 8.6 – Образование горизонтальной трещины путем закачки в нее нефильтрующейся жидкости:
1 – скважина, 2 – трещина
Совместное решение задачи теории упругости и гидравлики показывает, что с течением времени 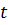 величина давления жидкости в скважине
величина давления жидкости в скважине  приближается к величине вертикальной компоненты горного давления
приближается к величине вертикальной компоненты горного давления  , но никогда не сравнивается с ней. Давление жидкости в скважине при малых
, но никогда не сравнивается с ней. Давление жидкости в скважине при малых  определяется формулой
определяется формулой
 | (8.14) |
где  – объем жидкости в трещине.
– объем жидкости в трещине.
Между объемом жидкости в трещине  и радиусом трещины также при малых
и радиусом трещины также при малых  существует зависимость
существует зависимость
 | (8.15) |
А максимальная ширина трещины
 | (8.16) |
Образование вертикальной трещины в результате закачки нефильтрующейся жидкости
Так же определяются параметры вертикальной трещины, образующейся при закачке в нее абсолютно нефильтрующейся жидкости. В этом случае давление жидкости в скважине  при малых величинах
при малых величинах  зависит от объема введенной в трещину жидкости,
зависит от объема введенной в трещину жидкости,  и других параметров следующим образом
и других параметров следующим образом
 | (8.17) |
Аналогично максимальная ширина трещины и ее полудлина определяются формулами
  | (8.18) |
где  - мощность пласта.
- мощность пласта.
