Граничное условие на поверхности твердых тел для идеальной жидкости

Границы области, занятой жидкостью, бывают двух типов (рисунок 5.3):

1) Твердые (границы твердых тел, движущихся в жидкости);

2) Свободные, форма которых заранее не известна (например, покрытая волнами поверхность моря).

Граничное условие на поверхности твердого тела в идеальной жидкости называется условием непроницаемости и записывается в виде:

где - проекция скорости жидкости на нормаль к поверхности тела;

- нормальная составляющая скорости рассматриваемой точки поверхности тела.

Свободная поверхность

Твердые границы

Рисунок 5.3 – Свободные поверхности и твердые границы.

Это условие означает, что жидкость не проникает внутрь тела и не отрывается от него. Если тело неподвижно, то условие непроницаемости на его поверхности имеет вид

Другим типом границ являются так называемые свободные поверхности, положение и движение которых заранее не известны, но известны силы, действующие на них. Примерами свободных поверхностей являются поверхность воды в реке или в море, а также границы струй.

Для идеальных жидкостей и газов граничными условиями на свободной поверхности, уравнение которой запишем в виде ( - неизвестная, подлежащая определению функция времени и координат) являются следующие два условия:

а) кинематическое условие:

или, что равносильно, при ,

где - скорость границы по нормали к ней;

б) динамическое условие

при ,

где – заданное давление внешней среды на поверхности жидкости.

Несжимаемая идеальная жидкость. Полная система уравнений

Несжимаемая жидкость–это жидкость, в каждой индивидуальной частице которой .

Отметим, что 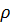может иметь различные значения для разных частиц, если среда неоднородная, поэтому в разных точках пространства в разные моменты времени плотность может быть разной – в зависимости от того, какая частица находится в данный момент в рассматриваемой точке. Следовательно, в несжимаемой, но неоднородной жидкости при эйлеровом описании плотность может зависеть от координат и времени. Условие несжимаемости можно записать в виде:

Если раскрыть полную производную по времени , получим

Система уравнений несжимаемой идеальной жидкости состоит из следующих уравнений:

	- условие несжимаемости	(5.6)
	- уравнение неразрывности	(5.7)
	- уравнение Эйлера	(5.8)
	- уравнение притока тепла	(5.9)
	- второй закон термодинамики	(5.10)
	- выражение для плотности внутренней энергии	(5.11)
	- формула для притока тепла по закону Фурье.	(5.12)

Уравнения (5.6)-(6.8) представляют собой систему механических уравнений, а уравнения (5.9)-(5.12) систему термодинамических уравнений.

Система механических уравнений замкнута. Она содержит в случае неоднородной жидкости 5 неизвестных и 5 уравнений. Для однородной жидкости 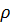- известная константа, одинаковая во всех частицах, тогда имеем 4 неизвестных 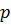и 4 уравнения (5.7),(5.8).

Модель вязкой жидкости

Вязкость – одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой.

Жидкость или газ называются вязкими, если компоненты тензора напряжений в них представляются в виде (система координат - декартова):

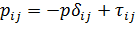(5.13)

где 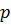- давление,

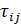- компоненты тензора вязких напряжений, которые являются функциями компонент тензора скоростей деформаций 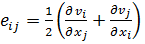и температуры 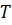и обращаются в нуль, если все компоненты тензора скоростей деформаций равны нулю.

Жидкость или газ называются линейно-вязкими, если компоненты тензора вязких напряжений в них зависят от компонент тензора скоростей деформаций линейно, то есть

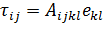(5.14)

Коэффициенты 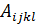называются коэффициентами вязкости.

Движение изотропной несжимаемой линейно-вязкой жидкости описывается уравнением Навье-Стокса

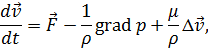(5.15)

где 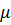– динамический коэффициент вязкости.

Можно также записать в виде:

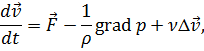(5.16)

где 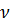– кинематический коэффициент вязкости.

Уравнение притока тепла для вязкой теплопроводной жидкости или газа имеет вид

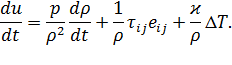(5.17)

Это уравнение написано при условии, что приток тепла происходит только за счет теплопроводности, процесс теплопроводности подчиняется закону Фурье

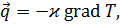
и коэффициент теплопроводности 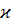- константа. Плотность внутренней энергии 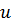является в общем случае функцией плотности 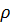и температуры 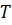. Для совершенного газа

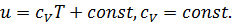
Для несжимаемой жидкости 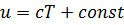, где 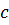- удельная теплоемкость.

Уравнение (5.17) обычно используется для расчета температуры в потоке. При этом типичными граничными условиями на стенках – границах потока являются либо условие, что температура жидкости на стенке равна заданной температуре стенки

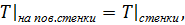
либо условие, что нормальная составляющая вектора потока тепла на стенке равна нулю

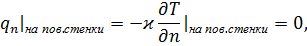
если стенка теплоизолирована.

Система уравнений, описывающая движение вязкой жидкости, очень сложна. Она нелинейная и содержит высшие производные от искомых функций. Для некоторых классов движений эту систему можно заменить более простой. А именно, для медленных течений, для которых выполнено условие 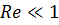можно пренебречь нелинейными членами, входящими в выражение для ускорений, по сравнению с членами, связанными с вязкостью. Тогда уравнения Навье-Стокса превращаются в линейные уравнения, называемые уравнениями Стокса. Число 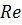, называемое числом Рейнольдса, по определению представляет собой следующую комбинацию

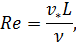
где 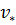, 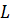– характерные скорость и линейный масштаб задачи (например, линейный размер обтекаемого тела);

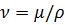- коэффициент кинематической вязкости.

Для быстрых движений маловязкой жидкости, при 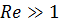, «вязкие члены» в уравнениях Навье-Стокса относительно малы. Однако полностью пренебречь ими (то есть пользоваться уравнениями идеальной жидкости) для всей области течения нельзя: граничные условия прилипания не зависят от величины числа 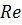(в частности, от величины коэффициента вязкости) и невозможно найти решения уравнений Эйлера, удовлетворяющие этим граничным условиям. При больших 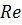вблизи границ возможно образование тонкого пограничного слоя, внутри которого вязкость существенно влияет на течение, а вне – может не учитываться. Уравнения Навье-Стокса при описании такого движения могут быть заменены более простыми уравнениями пограничного слоя.

Другое явление, которое наблюдается при больших значениях числа Рейнольдса, - это турбулентность. При достаточно больших числах Рейнольдса течения, как правило, имеют сложный хаотический характер: все характеристики хаотически пульсируют на фоне некоторых регулярных значений. Расчет турбулентных течений с помощью уравнений Навье-Стокса возможен только с помощью ЭВМ, причем при современном состоянии компьютерной техники – только при относительно небольших числах Рейнольдса. На практике расчет турбулентных течений проводится на основе так называемых полуэмпирических моделей.