Силы, действующие на сплошную среду. Вектор напряжения

Силы, действующие на сплошную среду, делятся на массовые и поверхностные.

Массовые силы – это силы, которые действуют на каждую частицу внутри среды, и для малой частицы сила пропорциональна ее массе.

Примеры массовых сил: силы тяжести, электромагнитные силы.

Пусть 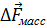– массовая сила, которая действует на малый объем с массой 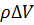. Введем плотность массовых сил 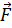(то есть силу, приходящуюся на единицу массы) так:

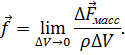(3.1)

На бесконечно малую частицу с массой 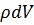действует массовая сила 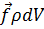. Сумма массовых сил, действующих на весь объем 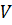, равна .

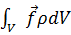Например, для плотности сил тяжести имеем:

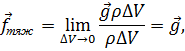
где 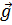– ускорение силы тяжести.

Поверхностные силы – это силы, приложенные в точках поверхности среды; для малого элемента поверхности они пропорциональны площади этого элемента.

Примеры поверхностных сил: давление, трение.

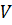Пусть – поверхность объема (рисунок 3.1). Обозначим через 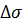малый элемент поверхности, 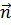- нормаль к этому элементу поверхности, направленная во внешнюю сторону, то есть в ту сторону, откуда действует внешняя сила. Пусть к этой площадке 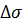приложена поверхностная сила .

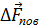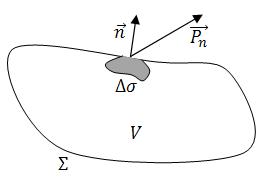
Рисунок 3.1 – Вектор напряжений

Плотность поверхностной силы или вектор напряжений

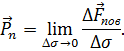(3.2)

Подчеркнем, что индекс 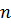в обозначении 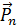указывает лишь ориентацию площадки (определяемую вектором нормали 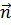к ней), на которой действуют векторы 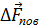и 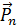, а не направление этих векторов. В общем случае 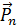не направлен по нормали к площадке. Например, если поверхностная сила на площадке с нормалью 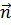есть сила трения, то 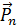направлен по касательной к этой площадке. Нормаль считается направленной во внешнюю сторону по отношению к части среды.

Поверхностная сила, действующая на бесконечно малую площадку с нормалью 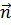и площадью 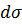равна 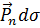, а суммарная поверхностная сила, действующая на всю поверхность , равна .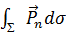

Тензор напряжений

Пусть на некоторую площадку с нормалью 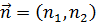действует сила, вызванная напряжением 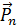(для простоты будем рассматривать двумерную модель). Рассмотрим векторы напряжений на площадках, нормали к которым параллельны координатным осям декартовой ортогональной системы координат, то есть на площадках с нормалями 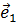, 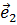. Обозначим эти векторы 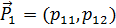, 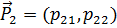соответственно (рисунок 3.2). Компоненты векторов 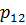, 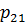будем называть касательными напряжениями, а компоненты 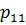, 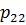– нормальными.

Примечание: В обозначении 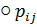первый индекс ( 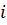) указывает направление нормали к площадке, на которую действует компонента напряжения, а второй ( 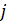) – по какой оси направлена эта же компонента напряжения.

Для касательных напряжений: 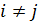. Пример: ( , ).

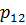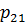Для нормальных напряжений: 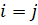. Пример: ( , ).

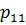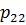Заметим, что компоненты вектора нормали совпадают с направляющими косинусами (рисунок 3.2), тогда верны следующие соотношения: ; .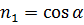

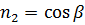Закон сохранения сил для элемента сплошной среды будет выглядеть следующим образом:

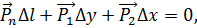(3.3)

где 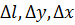– площадь элементов, на которые действуют вектора напряжений 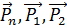соответственно.

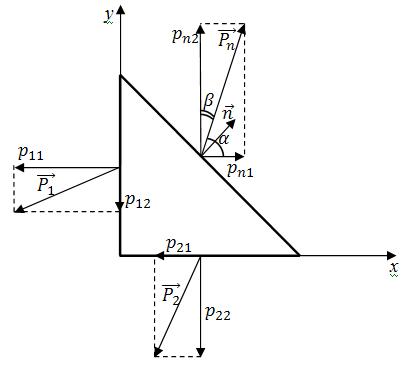
Рисунок 3.2 – Векторы напряжений на координатных площадках и на площадке с нормалью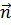

Перепишем (4.3) в проекциях на координатные оси:

:

:

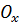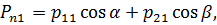
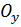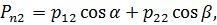
что эквивалентно записи:

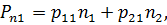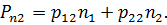(3.4)

Обобщив (3.4) на случай трехмерного пространства, получим:

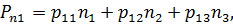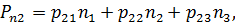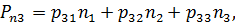(3.5)

или в векторной форме записи:

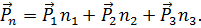(3.6)

где 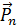– вектор напряжения на площадке с нормалью ;

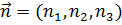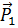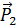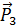, , - векторы напряжений на площадках, нормали к которым параллельны координатным осям декартовой ортогональной системы координат.

Соотношение (3.6) представляет собой формулу Коши. Из формулы (3.6) следует, что, если известны компоненты векторов напряжений, действующих на площадках, перпендикулярных координатным осям, то можно найти вектор напряжений, действующий на любой площадке, проходящей через заданную точку. Таким образом, верно следующее утверждение.

В краткой записи формулу Коши можно записать:

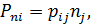(3.7)

где 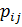– компоненты векторов напряжения 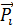, действующих на координатных площадках.

Эта формула показывает, что величины 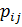являются компонентами тензора второго ранга (теорема деления из теории тензоров). Этот тензор называется тензором напряжений.Компоненты тензора напряжений записываются в виде матрицы, в которой первый столбец состоит из компонент вектора 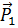, второй – из компонент вектора 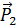, третий – из компонент вектора ,

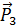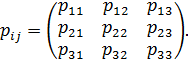
Замечание. Во многих книгах, особенно касающихся теории твердых деформируемых, например, упругих сред компоненты тензора напряжений обозначаются не 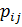, а 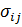. Обозначение 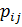ассоциируется с первой буквой слова pressure – давление, а 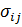- с первой буквой слова stress – напряжение.

Из формулы Коши (3.6) видно, что если 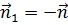, то

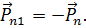
Из закона сохранения момента количества движения при отсутствии внутренних моментов количества движения и моментных взаимодействий следует, что тензор напряжения симметричен:

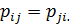
Недиагональные элементы матрицы компонент тензора напряжений – это касательные напряжения, а элементы, стоящие на главной диагонали – нормальные напряжения на координатных площадках.

ЭЛЕМЕНТЫ ТЕОРИИ ДЕФОРМАЦИЙ

Тензор деформаций

От приложенной нагрузки сплошная среда, как правило, деформируется. При деформации тело меняет свою форму и объем, т.е. меняются расстояния между его точками.

Деформация – это изменение длин всевозможных материальных отрезков и углов между ними.

Следовательно, говоря о деформациях, мы сравниваем длины материальных отрезков в двух состояниях – начальном и конечном, деформированном. В разных частях тела деформации могут быть разными. Поэтому при введении тензора деформации мы рассматриваем малую окрестность некоторой произвольной точки 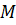сплошной среды (рисунок 4.1).

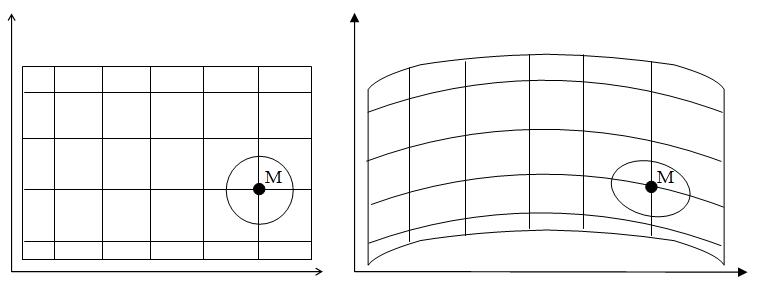
Рисунок 4.1 – Схематическое изображение начального (слева) и конечного (справа) положения точки М.

Пусть M' – какая-то точка из малой окрестности точки M (рисунок 4.2). Составим следующую таблицу.

	Начальное состояние	Конечное состояние
Координаты т.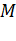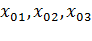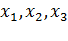
Координаты т.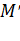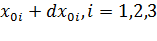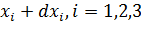
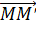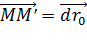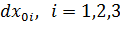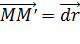Вектор	его компоненты:	его компоненты: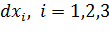
Квадрат длины отрезка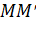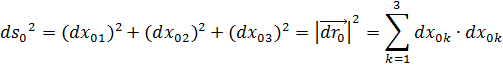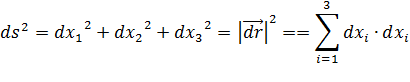

Рассмотрим разность квадратов длин отрезка 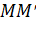в конечном и начальном состояниях :

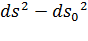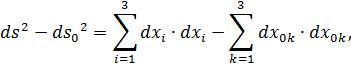
где

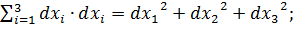
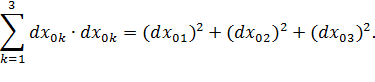
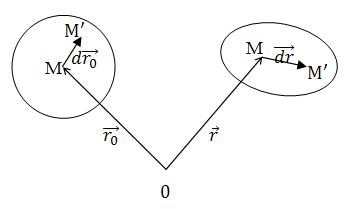
Рисунок 4.2 – Начальное и конечное положение точек М и M'

Пусть мы знаем, куда пришла каждая точка при деформации, то есть знаем координаты 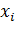после деформации как функции координат до деформации: .

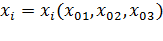Тогда,

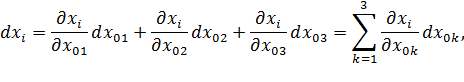
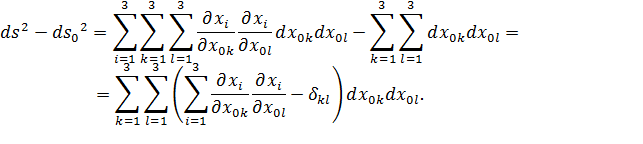(4.1)

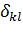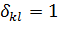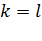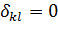где - символы Кронекера, при , при .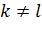

Введем следующее обозначение:

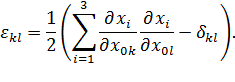(4.2)

Тензор с компонентами 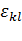, определенными формулами (4.2), называется тензором деформации и может быть записан в виде матрицы следующего вида:

Формулу (4.1) можно переписать в виде:

.

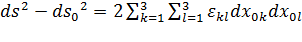(4.3)

Обсудим следующие 2 вопроса.

1. Почему 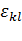действительно описывают деформации?

2. Зачем нужна 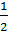в определении по формуле (4.2)?

Ответ на первый вопрос основан на соотношении (4.3). Из этого соотношения видно, что если 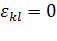для всех 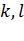, то 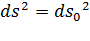, то есть длины всех отрезков не меняются, деформации нет. И наоборот, если для любых 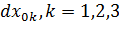имеем 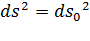, то все 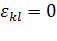. Наконец, и это главное, если 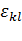известны, и выбран какой-то отрезок до деформации (т.е. известны 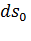и 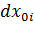), то длина этого отрезка после деформации 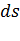вычисляется по формуле (4.3).

Ответ на второй вопрос найдем, когда будем рассматривать механический смысл компонент 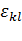.