Предмет и методы механики сплошных сред. некоторые сведения о векторном анализе

ПРЕДМЕТ И МЕТОДЫ МЕХАНИКИ СПЛОШНЫХ СРЕД. НЕКОТОРЫЕ СВЕДЕНИЯ О ВЕКТОРНОМ АНАЛИЗЕ

Механика сплошных сред (МСС)–наука о движении газообразных, жидких и твердых деформируемых тел.

В курсе теоретической механике студентами изучается движение материальной точки, дискретных систем материальных точек и абсолютно твердого тела. В механике сплошных сред же, с помощью и на основе методов, развитых в теоретической механике, рассматривается движение материальных тел, которые заполняют объем непрерывно (сплошным образом) и расстояние между точками которых во время движения может изменяться.

Помимо жидкостей, газов и деформируемых тел, в механике сплошных сред рассматриваются также особые среды – поля (электромагнитное поле, поле излучений, гравитационное поле и т.д.). Почему столь различные по своим физическим свойствам среды изучаются в одной науке? Потому что основным методом в механике сплошных сред является математическое моделирование, то есть введение количественных характеристик явления, составление уравнений, решение которых позволяет рассчитать эти характеристики в каждом конкретном случае, а также выявить общие закономерности рассматриваемого класса явлений. Эти уравнения оказываются качественно одинаковыми для сред различной природы, так как они основаны на универсальных физических законах, таких как закон сохранения массы или закон сохранения импульса. В механике сплошных сред как раз и выводятся прежде всего эти универсальные уравнения, а затем и уравнения, которые применяются для частных классов сред.

Существуют отдельные науки, в которых изучается только движение жидкостей (гидромеханика), или газов (газовая динамика), или твердых деформируемых сред (сопротивление материалов, теория упругости, теория пластичности), или движение под действием электромагнитного поля (магнитная гидродинамика) и другие. Механика сплошных сред содержит общие основы всех этих наук и дает представление о том, как надо строить математические модели новых материалов, с новыми, иногда только еще проектируемыми свойствами.

Предметом механики сплошных сред является математическое моделирование движения, равновесия, силовых взаимодействий различных сред.

Сплошная среда– это среда, заполняющая занятую ею область непрерывно, то есть в любом сколь угодно малом объеме этой области содержится масса.

Некоторые сведения о векторном анализе

Все физические величины можно разделить на три группы: скаляры, векторы и тензоры.

Скаляр – это величина, каждое значение которой может быть выражено одним числом.

Векторной величиной называется величина, представляющая собой одновременно и число, и направление (скорость, ускорение).

Тензор – это объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются скаляры (тензор нулевого ранга), векторы (тензор первого ранга), матрицы (тензор второго ранга) и т.п.

Градиент

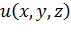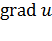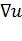Градиентом скалярного поля называется вектор, обозначаемый или , проекциями которого на оси координат служат значения частных производных :

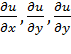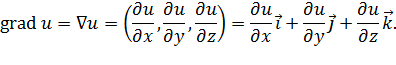
Физический смысл: Градиент функции есть вектор, направление которого указывает направление наибыстрейшего возрастания функции 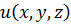, а его модуль равен наибольшей скорости изменения функции в определенной точке.

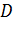Если в каждой точке области задан определенный вектор, то говорят, что в этой области задано векторное поле.

Поток вектора

Пусть векторное поле образовано вектором .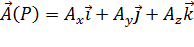

Возьмем в этом поле некоторую поверхность 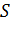и выберем на ней определенную сторону. Обозначим через 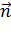единичный вектор нормали к рассматриваемой стороне поверхности в произвольной ее точке; проекциями вектора 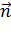служат направляющие косинусы нормали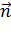 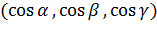. Рассмотрим интеграл по поверхности S от скалярного произведения вектора поля А(Р) на единичный вектор нормали n:

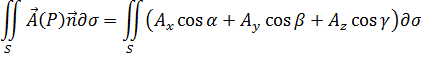		(1.1)

Если 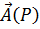– поле скоростей текущей жидкости, то интеграл (1.1) выражает поток жидкости через поверхность S. В произвольном векторном поле интеграл (1.1) будем называть потоком вектора через поверхность 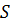и обозначим буквой .

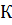Потоком вектора 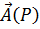через поверхность 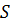называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали 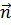к поверхности:

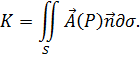
Таким образом, вычисление потока вектора сводится к вычислению интеграла по поверхности. Из определения следует, что поток вектора 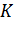– величина скалярная. Если изменить направление нормали 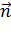на противоположное, т.е. переменить сторону поверхности 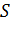, то поток 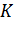изменит знак.

Особый интерес представляет случай, когда 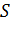– замкнутая поверхность, ограничивающая некоторую область 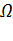. Если рассматривается внешняя нормаль, то мы будем говорить о потоке изнутри поверхности 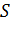. Он обозначается так:

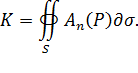
Когда векторное поле 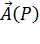представляет поле скоростей жидкости, величина потока К дает разность между количеством жидкости, вытекающей из области Ω, и количеством жидкости, поступающей в эту область.

Если 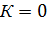, то в область 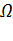жидкости втекает столько же, сколько и вытекает. Так, например, будет для любой области, расположенной в потоке воды, текущей в реке.

Если же величина 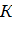отлична от 0, например, положительная, то из области 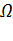жидкости вытекает больше, чем втекает. Это означает, что в области 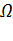имеются источники, питающие поток жидкости. Наоборот, если величина 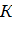отрицательна, то это указывает на наличие стоков – мест, где жидкость удаляется из потока.

Дивергенция

Рассмотрим некоторую точку 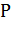векторного поля 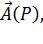находящуюся внутри области, ограниченной замкнутой поверхностью 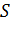, целиком содержащейся в поле. Вычислим поток вектора через поверхность 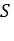и возьмем отношение этого потока к объему 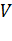области 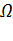, ограниченной поверхностью :

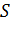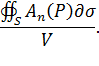
В поле скоростей жидкости это отношение определяет количество жидкости, возникающее в единицу времени в области 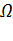, отнесенное к единице объема, т.е., как говорят, среднюю объемную мощность источника; если поток изнутри поверхности 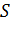меньше 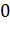, то соответственно говорят о мощности стока.

Найдем теперь предел отношения

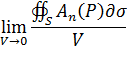
при условии, что область 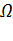стягивается в точку 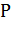, т.е., 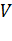стремится к .

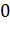Если этот предел положителен, то точка 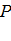называется источником, а если отрицателен, то стоком. Сама величина предела характеризует мощность источника или стока. В первом случае в любом бесконечно малом объеме, окружающем точку 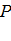, жидкость возникает, а во втором случае исчезает. Предел этот называется дивергенцией или расходимостью векторного поля в точке .

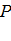Дивергенцией, или расходимостью векторного поля 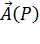в точке называется предел отношения потока вектора через поверхность, окружающую точку , к объему, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в точку .

Дивергенцию поля обозначают символом 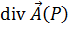. Таким образом,

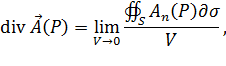
где предел вычисляется при условии, что поверхность 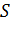стягивается к точке .

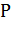Математически дивергенцию можно выразить следующим образом:

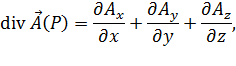
где значения частных производных берутся в точке .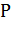

Циркуляция

Пусть векторное поле образовано вектором .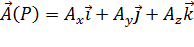

Возьмем в этом поле некоторую линию 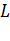и выберем на ней определенное направление. Обозначим через 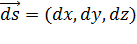вектор, имеющий направление касательной к линии и по модулю равный дифференциалу длины дуги. Направление касательной считается совпадающим с выбранным направлением на линии.

Рассмотрим криволинейный интеграл по линии 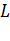от скалярного произведения векторов 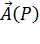и :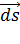

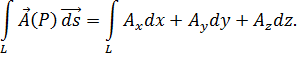		(1.2)

В силовом поле интеграл (1.2) выражает работу при перемещении материальной точки вдоль линии .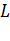

Если 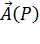– произвольное векторное поле, а 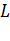– замкнутый контур, то интеграл (1.2) носит специальное название – циркуляция вектора.

Циркуляцией вектора 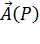вдоль замкнутого контура 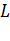называется криволинейный интеграл по этому контуру от скалярного произведения вектора 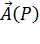на вектор 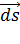касательной к контуру:

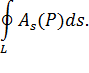
Физический смысл циркуляции вектора в случае, когда 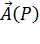– поле скоростей текущей жидкости: примем для простоты, что контур 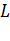- окружность, расположенная в некоторой плоскости. Предположим, что окружность является периферией колесика с радиальными лопатками, способного вращаться вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Если циркуляция будет равна 0, то колесико будет оставаться неподвижным: силы, действующие на лопатки, уравновешивают друг друга. Если циркуляция не равна 0, то колесико будет вращаться, причем тем быстрее, чем больше величина циркуляции.

Ротор

Ротором векторного поля или вихрем 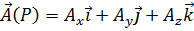называется вектор

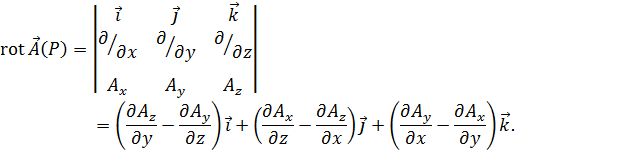
Проекция 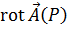этого вектора на любое направление дает предел отношения циркуляции вектора поля по контуру, лежащему в плоскости, проходящей через точку 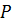, к площади, ограниченной этим контуром. Этот предел будет наибольшим в том случае, когда направление нормали 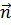совпадает с направлением .

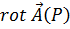Введенные нами основные понятия векторного анализа: градиент, дивергенция, ротор удобно представлять с помощью символического вектора 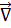(«набла-вектор»), называемого оператором Гамильтона (Гамильтонианом):

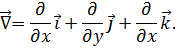
1. Произведение набла-вектора 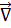на скалярную функцию 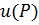дает градиент этой функции:

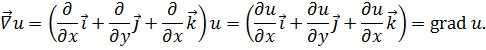
2. Скалярное произведение набла-вектора 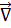на векторную функцию 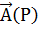дает дивергенцию этой функции:

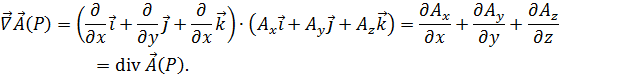
3. Векторное произведение набла-вектора 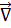на векторную функцию 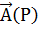дает ротор этой функции:

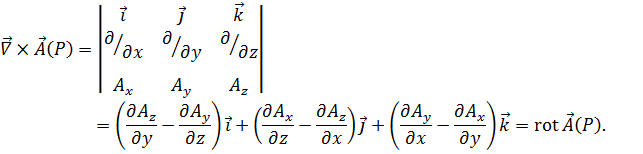
Оператор Лапласа–это оператор вида:

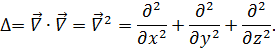
Линии тока и траектории

Понятие линий тока используется при эйлеровом описании движения среды, в основном при описании движения жидкостей и газов.

Линия тока - это линия, которая определяется для фиксированного момента времени и обладает тем свойством, что в каждой ее точке направление касательной совпадает с направлением вектора скорости среды. Отметим, что в рассматриваемый момент времени в разных точках линии тока находятся разные частицы.

Понятие траектории связано с лагранжевым подходом к описанию движения.

Траектория – это путь индивидуальной частицы; в каждой точке траектории направление касательной к траектории совпадает с направлением вектора скорости. Но здесь имеется в виду скорости одной и той же частицы в разные моменты времени, в то время как, говоря о линии тока, мы рассматриваем скорости разных частиц в один и тот же момент времени.

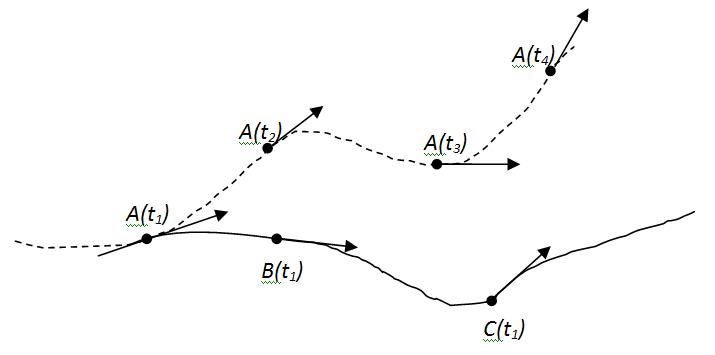
Рисунок 2.5 – Сплошная линия – линия тока в момент времени 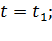пунктир – траектория точки А

Тензор напряжений

Пусть на некоторую площадку с нормалью 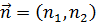действует сила, вызванная напряжением 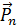(для простоты будем рассматривать двумерную модель). Рассмотрим векторы напряжений на площадках, нормали к которым параллельны координатным осям декартовой ортогональной системы координат, то есть на площадках с нормалями 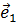, 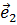. Обозначим эти векторы 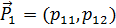, 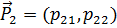соответственно (рисунок 3.2). Компоненты векторов 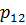, 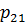будем называть касательными напряжениями, а компоненты 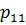, 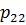– нормальными.

Примечание: В обозначении 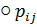первый индекс ( 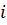) указывает направление нормали к площадке, на которую действует компонента напряжения, а второй ( 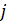) – по какой оси направлена эта же компонента напряжения.

Для касательных напряжений: 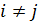. Пример: ( , ).

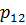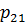Для нормальных напряжений: 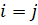. Пример: ( , ).

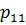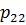Заметим, что компоненты вектора нормали совпадают с направляющими косинусами (рисунок 3.2), тогда верны следующие соотношения: ; .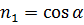

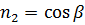Закон сохранения сил для элемента сплошной среды будет выглядеть следующим образом:

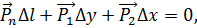(3.3)

где 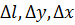– площадь элементов, на которые действуют вектора напряжений 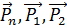соответственно.

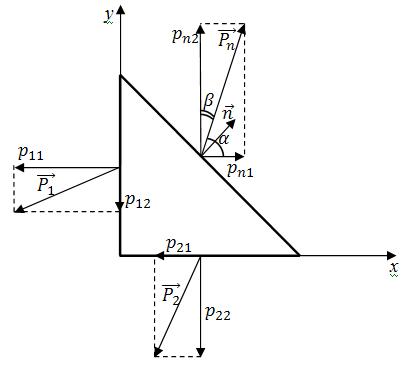
Рисунок 3.2 – Векторы напряжений на координатных площадках и на площадке с нормалью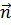

Перепишем (4.3) в проекциях на координатные оси:

:

:

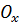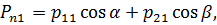
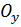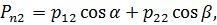
что эквивалентно записи:

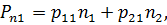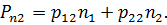(3.4)

Обобщив (3.4) на случай трехмерного пространства, получим:

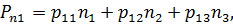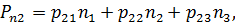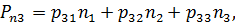(3.5)

или в векторной форме записи:

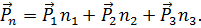(3.6)

где 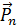– вектор напряжения на площадке с нормалью ;

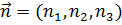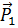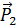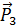, , - векторы напряжений на площадках, нормали к которым параллельны координатным осям декартовой ортогональной системы координат.

Соотношение (3.6) представляет собой формулу Коши. Из формулы (3.6) следует, что, если известны компоненты векторов напряжений, действующих на площадках, перпендикулярных координатным осям, то можно найти вектор напряжений, действующий на любой площадке, проходящей через заданную точку. Таким образом, верно следующее утверждение.

В краткой записи формулу Коши можно записать:

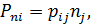(3.7)

где 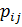– компоненты векторов напряжения 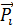, действующих на координатных площадках.

Эта формула показывает, что величины 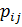являются компонентами тензора второго ранга (теорема деления из теории тензоров). Этот тензор называется тензором напряжений.Компоненты тензора напряжений записываются в виде матрицы, в которой первый столбец состоит из компонент вектора 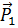, второй – из компонент вектора 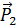, третий – из компонент вектора ,

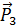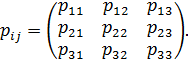
Замечание. Во многих книгах, особенно касающихся теории твердых деформируемых, например, упругих сред компоненты тензора напряжений обозначаются не 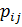, а 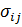. Обозначение 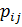ассоциируется с первой буквой слова pressure – давление, а 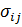- с первой буквой слова stress – напряжение.

Из формулы Коши (3.6) видно, что если 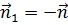, то

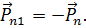
Из закона сохранения момента количества движения при отсутствии внутренних моментов количества движения и моментных взаимодействий следует, что тензор напряжения симметричен:

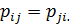
Недиагональные элементы матрицы компонент тензора напряжений – это касательные напряжения, а элементы, стоящие на главной диагонали – нормальные напряжения на координатных площадках.

ЭЛЕМЕНТЫ ТЕОРИИ ДЕФОРМАЦИЙ

Тензор деформаций

От приложенной нагрузки сплошная среда, как правило, деформируется. При деформации тело меняет свою форму и объем, т.е. меняются расстояния между его точками.

Деформация – это изменение длин всевозможных материальных отрезков и углов между ними.

Следовательно, говоря о деформациях, мы сравниваем длины материальных отрезков в двух состояниях – начальном и конечном, деформированном. В разных частях тела деформации могут быть разными. Поэтому при введении тензора деформации мы рассматриваем малую окрестность некоторой произвольной точки 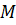сплошной среды (рисунок 4.1).

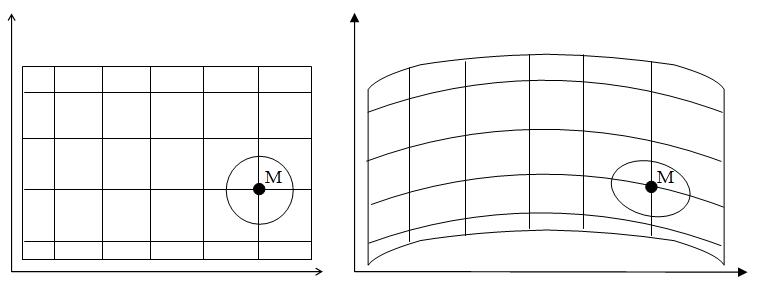
Рисунок 4.1 – Схематическое изображение начального (слева) и конечного (справа) положения точки М.

Пусть M' – какая-то точка из малой окрестности точки M (рисунок 4.2). Составим следующую таблицу.

	Начальное состояние	Конечное состояние
Координаты т.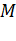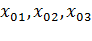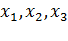
Координаты т.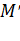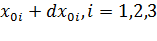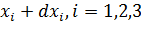
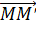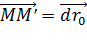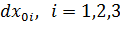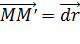Вектор	его компоненты:	его компоненты: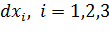
Квадрат длины отрезка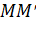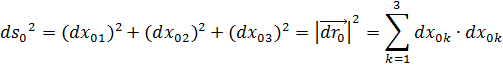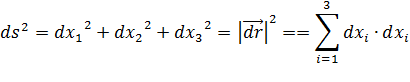

Рассмотрим разность квадратов длин отрезка 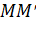в конечном и начальном состояниях :

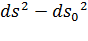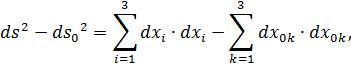
где

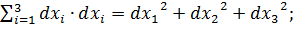
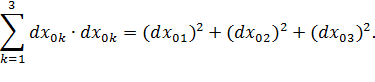
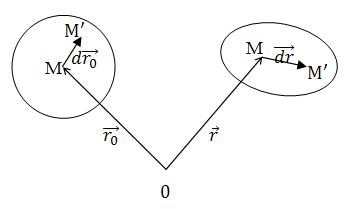
Рисунок 4.2 – Начальное и конечное положение точек М и M'

Пусть мы знаем, куда пришла каждая точка при деформации, то есть знаем координаты 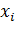после деформации как функции координат до деформации: .

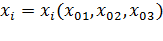Тогда,

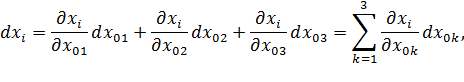
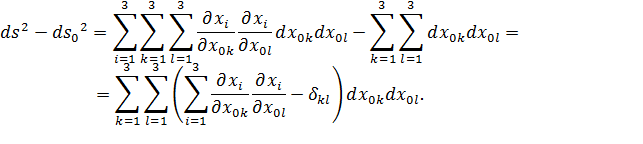(4.1)

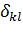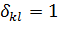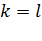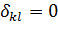где - символы Кронекера, при , при .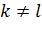

Введем следующее обозначение:

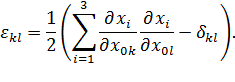(4.2)

Тензор с компонентами 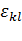, определенными формулами (4.2), называется тензором деформации и может быть записан в виде матрицы следующего вида:

Формулу (4.1) можно переписать в виде:

.

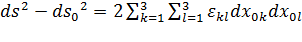(4.3)

Обсудим следующие 2 вопроса.

1. Почему 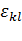действительно описывают деформации?

2. Зачем нужна 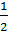в определении по формуле (4.2)?

Ответ на первый вопрос основан на соотношении (4.3). Из этого соотношения видно, что если 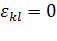для всех 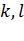, то 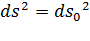, то есть длины всех отрезков не меняются, деформации нет. И наоборот, если для любых 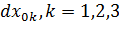имеем 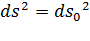, то все 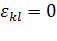. Наконец, и это главное, если 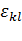известны, и выбран какой-то отрезок до деформации (т.е. известны 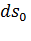и 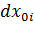), то длина этого отрезка после деформации 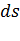вычисляется по формуле (4.3).

Ответ на второй вопрос найдем, когда будем рассматривать механический смысл компонент .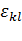

Модель вязкой жидкости

Вязкость – одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой.

Жидкость или газ называются вязкими, если компоненты тензора напряжений в них представляются в виде (система координат - декартова):

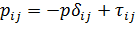(5.13)

где 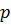- давление,

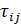- компоненты тензора вязких напряжений, которые являются функциями компонент тензора скоростей деформаций 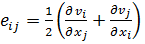и температуры 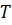и обращаются в нуль, если все компоненты тензора скоростей деформаций равны нулю.

Жидкость или газ называются линейно-вязкими, если компоненты тензора вязких напряжений в них зависят от компонент тензора скоростей деформаций линейно, то есть

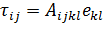(5.14)

Коэффициенты 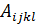называются коэффициентами вязкости.

Движение изотропной несжимаемой линейно-вязкой жидкости описывается уравнением Навье-Стокса

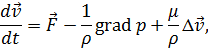(5.15)

где 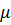– динамический коэффициент вязкости.

Можно также записать в виде:

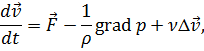(5.16)

где 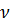– кинематический коэффициент вязкости.

Уравнение притока тепла для вязкой теплопроводной жидкости или газа имеет вид

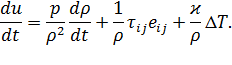(5.17)

Это уравнение написано при условии, что приток тепла происходит только за счет теплопроводности, процесс теплопроводности подчиняется закону Фурье

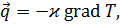
и коэффициент теплопроводности 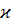- константа. Плотность внутренней энергии 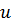является в общем случае функцией плотности 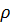и температуры 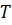. Для совершенного газа

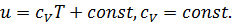
Для несжимаемой жидкости 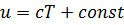, где 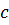- удельная теплоемкость.

Уравнение (5.17) обычно используется для расчета температуры в потоке. При этом типичными граничными условиями на стенках – границах потока являются либо условие, что температура жидкости на стенке равна заданной температуре стенки

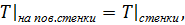
либо условие, что нормальная составляющая вектора потока тепла на стенке равна нулю

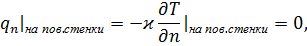
если стенка теплоизолирована.

Система уравнений, описывающая движение вязкой жидкости, очень сложна. Она нелинейная и содержит высшие производные от искомых функций. Для некоторых классов движений эту систему можно заменить более простой. А именно, для медленных течений, для которых выполнено условие 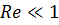можно пренебречь нелинейными членами, входящими в выражение для ускорений, по сравнению с членами, связанными с вязкостью. Тогда уравнения Навье-Стокса превращаются в линейные уравнения, называемые уравнениями Стокса. Число 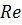, называемое числом Рейнольдса, по определению представляет собой следующую комбинацию

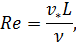
где 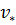, 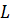– характерные скорость и линейный масштаб задачи (например, линейный размер обтекаемого тела);

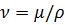- коэффициент кинематической вязкости.

Для быстрых движений маловязкой жидкости, при 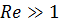, «вязкие члены» в уравнениях Навье-Стокса относительно малы. Однако полностью пренебречь ими (то есть пользоваться уравнениями идеальной жидкости) для всей области течения нельзя: граничные условия прилипания не зависят от величины числа 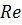(в частности, от величины коэффициента вязкости) и невозможно найти решения уравнений Эйлера, удовлетворяющие этим граничным условиям. При больших 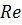вблизи границ возможно образование тонкого пограничного слоя, внутри которого вязкость существенно влияет на течение, а вне – может не учитываться. Уравнения Навье-Стокса при описании такого движения могут быть заменены более простыми уравнениями пограничного слоя.

Другое явление, которое наблюдается при больших значениях числа Рейнольдса, - это турбулентность. При достаточно больших числах Рейнольдса течения, как правило, имеют сложный хаотический характер: все характеристики хаотически пульсируют на фоне некоторых регулярных значений. Расчет турбулентных течений с помощью уравнений Навье-Стокса возможен только с помощью ЭВМ, причем при современном состоянии компьютерной техники – только при относительно небольших числах Рейнольдса. На практике расчет турбулентных течений проводится на основе так называемых полуэмпирических моделей.

Упругая деформация

Рассмотрим случай упругой деформации горных пород вблизи скважины, считая напряженное состояние одномерным, зависящим от радиуса 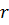(рис. 6.8). Уравнение равновесия упругой среды, определяющее радиальное смещение, имеет вид:

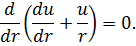
Распределение напряжений осесимметричное. При 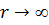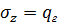, , 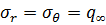а при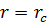 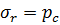. Тогда,

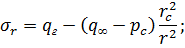
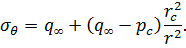
Эти выражения известны в теории упругости как формулы Лямэ. Есл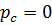и при 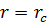, имеем ,

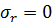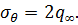
Пластическая деформация

Рассмотрим случай пластической деформации горных пород вблизи скважины, считая напряженное состояние одномерным, зависящим от радиуса 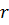(рис. 6.8). В этом случае напряжения 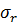и 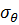связаны соотношением:

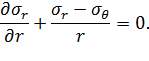(6.2)

Вертикальная компонента напряжения

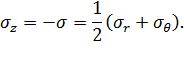(6.3)

В формуле (6.3) 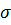— среднее нормальное напряжение.

Будем считать, что состояние пластичности наступает, когда максимальное касательное напряжение достигает постоянной предельной величины 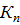, т. е.

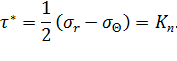(6.4)

Пусть радиус скважины составляет 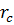, а среднее нормальное напряжение при 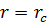равно .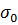

Подставим условие (6.4) в уравнение (6.2), получим систему уравнений:

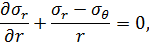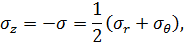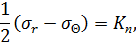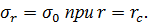(6.5)

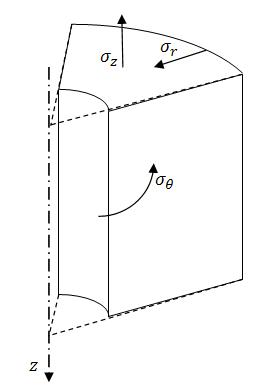
Рисунок 6.8 – Участок горной породы, прилегающий к скважине

Решая (6.5), получим следующие выражения для напряжений:

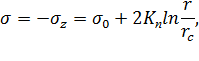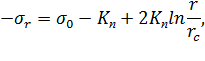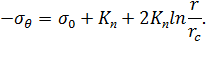(6.6)

Из (6.6) следует, что вбл