Использование калмановской фильтрации в нелинейных задачах
Данный раздел посвящен обсуждению применимости алгоритма калмановской фильтрации в условиях, когда модель движения и/или модель измерений являются нелинейными, то есть:
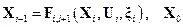 ,
,
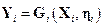 .
.
Очевидно, непосредственное использование фильтра Калмана в указанных условиях невозможно. Однако, линеаризуя каждую из моделей в окрестности т.н. опорной траектории, мы получим линейные модели в отклонениях от опорной траектории, к которым калмановские соотношения будут применимы. Таким образом, формально имеем:
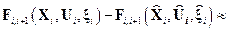
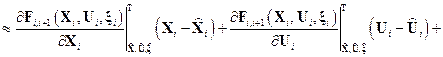
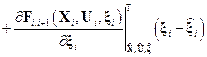
и
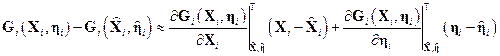 .
.
Положим 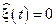 и
и 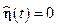 на опорной траектории, и введем следующие обозначения:
на опорной траектории, и введем следующие обозначения:
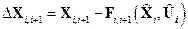 ;
; 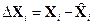 ;
; 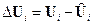 ;
;
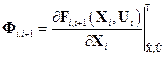 ;
; 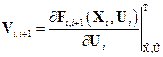 ;
; 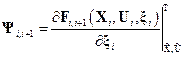 ;
;
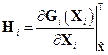 ;
; 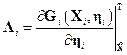 .
.
С учетом введенных обозначений линеаризованные модели эволюции и измерений могут быть переписаны следующим образом:
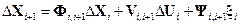 ,
,
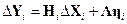 ,
,
Как видно, полученные линеаризованные модели с точностью до обозначений совпадают по начертанию с линейными моделями из начала раздела за исключением лишь матрицы 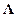 . Для получения более точного совпадения моделей можно обозначить
. Для получения более точного совпадения моделей можно обозначить 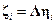 а соответствующую ковариационную матрицу в соотношениях коррекции –
а соответствующую ковариационную матрицу в соотношениях коррекции – 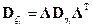 .
.
Таким образом, соотношения коррекции и прогноза примут вид:
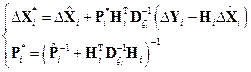
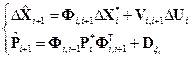
Несколько повысим вычислительную точность алгоритма путем замены разности 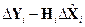 (в отклонениях от опорной траектории) на
(в отклонениях от опорной траектории) на 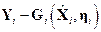 в соотношении коррекции для прращения фазового вектора системы, а также добавим к левой и правой частям этого уравнения значение вектора состояния на опорной траектории в
в соотношении коррекции для прращения фазового вектора системы, а также добавим к левой и правой частям этого уравнения значение вектора состояния на опорной траектории в 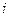 -й момент времени. Заменим также уравнение прогноза для приращения фазового вектора на соответствующее нелинейное соотношение из модели эволюции при нулевой случайной составляющей. В результате выполнения всех перечисленных выше действий преобразуем соотношения коррекции и прогноза к следующему виду:
-й момент времени. Заменим также уравнение прогноза для приращения фазового вектора на соответствующее нелинейное соотношение из модели эволюции при нулевой случайной составляющей. В результате выполнения всех перечисленных выше действий преобразуем соотношения коррекции и прогноза к следующему виду:
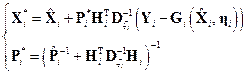
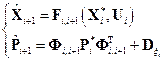
Опорная траектория фазового вектора системы, необходимая для вычисления значений матриц 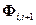 и
и 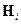 , полностью определяется первым из соотношений прогноза.
, полностью определяется первым из соотношений прогноза.
Метод наименьших квадратов
В настоящем разделе представлен метод наименьших квадратов, адаптированный для апостериорного анализа динамических систем.
Построение оценок
Для случая линейной модели равноточных измерений:
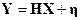
имеем следующий алгоритм оценивания фазового вектора:
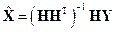 .
.
Для случая неравноточных измерений вводится в рассмотрение матрица 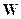 , содержащая на диагонали весовые коэффициенты. С учетом весовых коэффициентов предыдущее соотношение примет вид:
, содержащая на диагонали весовые коэффициенты. С учетом весовых коэффициентов предыдущее соотношение примет вид:
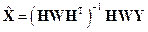 .
.
Если в качестве весовой использовать матрицу, обратную к ковариационной матрице ошибок измерений 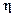 , то с учетом того обстоятельства, что
, то с учетом того обстоятельства, что 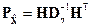 получим:
получим:
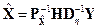 .
.
Как следует из приведенных выше соотношений, основу метода составляет матрица 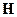 , связывающая оцениваемый фазовый вектор
, связывающая оцениваемый фазовый вектор 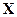 , отнесенный к некоторому моменту времени
, отнесенный к некоторому моменту времени 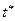 , и вектор измерений
, и вектор измерений 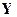 . Вектор
. Вектор 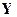 имеет, как правило, блочную структуру, в которой каждый из блоков отнесен к некоторому моменту времени
имеет, как правило, блочную структуру, в которой каждый из блоков отнесен к некоторому моменту времени 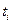 , не совпадающую в общем случае с
, не совпадающую в общем случае с 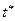 .
.
На рисунке показано некоторое возможное взаимное расположение моментов времени, к которым отнесены измерения и момента времени, к которому отнесен вектор оцениваемых параметров.
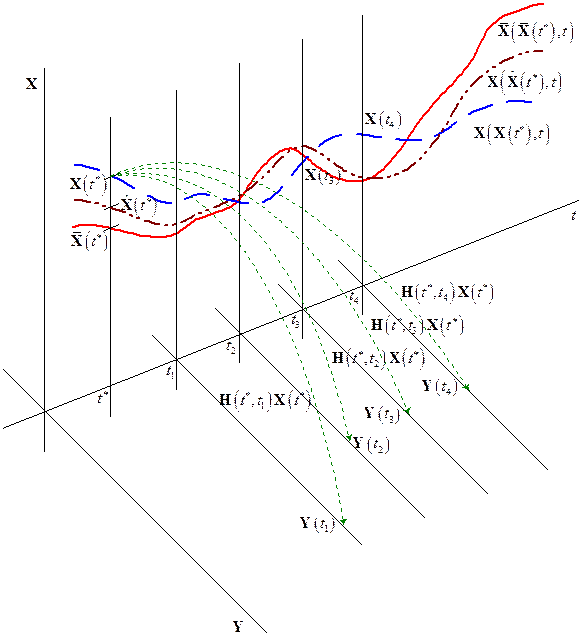
Для каждого вектора 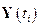 справедливо следующее соотношение:
справедливо следующее соотношение:
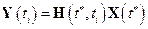 , при
, при 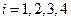 .
.
Таким образом, в результирующем соотношении метода наименьших квадратов вектор 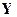 и матрица
и матрица 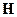 имеют следующую структуру:
имеют следующую структуру:
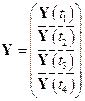 ;
; 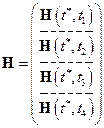 .
.
Каждый блок матрицы 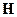 может быть построен как результат произведения матрицы Коши, определяющей переход для фазового вектора системы от момента времени
может быть построен как результат произведения матрицы Коши, определяющей переход для фазового вектора системы от момента времени 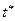 к моменту
к моменту 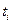 , и матрицы, связывающей фазовый вектор и блок вектора измерений, отнесенные к одному и тому же моменту времени
, и матрицы, связывающей фазовый вектор и блок вектора измерений, отнесенные к одному и тому же моменту времени 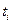 :
:
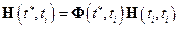 .
.
Предпочтительным, с точки зрения обеспечения максимальной точности оценивания, является размещение момента времени, к которому привязан вектор оцениваемых параметров, в непосредственной близости от моментов, к которым привязаны измерения.
Прогноз
Для прогнозирования значения фазового вектора линейной системы
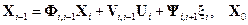 ,
,
где
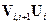 – определяет неслучайное вынуждающее воздействие на систему;
– определяет неслучайное вынуждающее воздействие на систему;
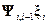 – определяет случайное воздействие на систему.
– определяет случайное воздействие на систему.
могут быть использованы соотношения прогноза, встречавшиеся выше при описании алгоритма калмановской фильтрации:
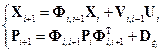
где 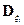 – ковариационная матрица вектора
– ковариационная матрица вектора 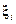 .
.
