Апостериорный анализ динамических систем

В настоящем разделе будут рассмотрены два метода: Фильтр Калмана и Метод наименьших квадратов, в применении к построению оценок фазового вектора динамической системы, координаты которого, как правило, недоступны для непосредственных измерений их значений, на основе статистической обработки искаженных результатов измерений некоторых других характеристик системы, функционально связанных с координатами ее фазового вектора.

Иными словами, мы будем восстанавливать совокупность значений фазового вектора на некотором временном интервале, путем обработки множества результатов измерений, искаженных ошибками. Очевидно, что совокупность компонент всех векторов состояния, подлежащих оцениванию, существенно превосходит количество результатов измерений, по которым мы будем строить оценки. Таким образом, мы получим систему уравнений, где количество неизвестных много больше количества уравнений, решить которую мы сможем, лишь выразив одни неизвестные через другие.

Однако если нам удастся связать совокупность векторов состояния некоторой функциональной зависимостью, позволяющей восстановить значение любого вектора состояния по значению одного из них (начальным условиям), то задача существенно упростится. Теперь мы должны оценить координаты только одного из векторов состояния, что устраняет неопределенность в задаче (или, по меньшей мере, снижает ее степень).

Важно отметить, что в процессе оценивания нам неизвестны, как точные значения координат фазового вектора[5], так и точный вид законов, связывающие фазовые векторы, отнесенные к разным моментам времени, между собой и с измеряемыми характеристиками.

Тем не менее, приблизительные зависимости, с той или иной степенью точности аппроксимирующие точные, могут быть построены. Кроме того, известны, как правило, бывают и некоторые приблизительные априорные значения компонент фазового вектора.

Функциональная зависимость между фазовыми векторами, отнесенными к разным моментам времени, носит название «модель движения» (или «модель эволюции» в общем случае). Функциональная связь подверженных измерению характеристик системы с оцениваемыми компонентами фазового вектора называется «модель измерений».

Фильтр Калмана

Модель движения

Как известно, Фильтр Калмана предназначен для оценивания вектора состояния 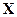линейной динамической системы, модель эволюции которого может быть записана в виде:

,

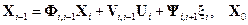где
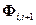– матрица Коши[6], определяющая изменение вектора состояния системы в ее собственном движении (без управляющих и шумовых воздействий) от момента времени 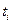к моменту времени ;
– вектор вынуждающих неслучайных воздействий на систему (например, управляющих воздействий) в момент времени ;
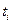– матрица влияния вынуждающих воздействий в момент времени 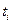на вектор состояния системы в момент времени ;
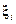– вектор случайных независимых центрированных воздействий на систему в момент времени ;
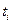– матрица влияния случайных воздействий в момент времени 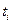на вектор состояния системы в момент времени .

Модель измерений

Оценивание выполняется на основе статистической обработки результатов измерений 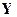, линейно связанных с вектором состояния 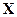, и искаженных аддитивной несмещенной ошибкой :

,

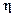где 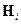– матрица, связывающая векторы состояния и измерений в один и тот же момент времени .

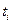Коррекция

Основу Фильтра Калмана составляют соотношения коррекции, являющиеся результатом минимизации следа ковариационной матрицы апостериорной плотности распределения линейной (по вектору измерений ) оценки вектора состояния системы :

где – ковариационная матрица вектора .

Прогноз

Дополняя соотношения коррекции соотношениями прогноза, основанными на линейных свойствах модели эволюции системы:

где – ковариационная матрица вектора 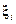, получим формулы рекуррентного байесовского алгоритма оценивания вектора состояния системы 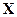и его ковариационной матрицы на основе статистической обработки результатов измерений .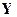

Оценивание

Очевидно, для реализации приведенных соотношений необходимо уметь строить матрицы 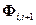, из модели эволюции, матрицу 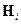из модели измерений, а также ковариационные матрицы и для каждого 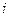-го момента времени.

Кроме того, для инициализации вычислительного процесса необходимо каким-либо образом определить апостериорные , или априорные , оценки вектора состояния и его ковариационной матрицы. Термин «априорные» или «апостериорные» в данном случае означает лишь то качество, в котором вектор состояния и его ковариационная матрица будут использованы в вычислительном алгоритме, и не говорит ничего о том, каким образом они были получены.

Таким образом, выбор соотношения, с которого следует начинать вычисления, определяется тем, к каким моментам времени отнесены начальные условия фильтраци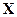и и и первый необработанный вектор измерений 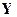. Если моменты времени совпадают, то первым следует применить соотношения коррекции, позволяющие уточнить начальные условия, если нет, то сначала следует спрогнозировать начальные условия к моменту привязки первого необработанного вектора измерений.

Поясним алгоритм калмановской фильтрации при помощи рисунка.

На рисунке в осях координат 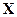, 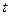(в канале движения) изображены несколько возможных траекторий фазового вектора :

– истинная траектория эволюции фазового вектора;
– эволюция фазового вектора, прогнозируемая на основе использования модели движения и априорной оценки фазового вектора , отнесенной к моменту времени ;
– эволюция фазового вектора, прогнозируемая на основе использования модели движения и апостериорной (более точной) оценки фазового вектора , отнесенной к моменту времени

В осях координат 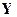, 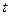(в канале измерений) в моменты времени и изображены результаты измерений и :

,

где
– истинное значение вектора измерений в момент времени ;
– вектор ошибок измерений, реализовавшихся в момент времени .

Для построения поправки к априорному фазовому вектору системы используется разность между результатом измерения и тем значением, которое было бы измерено согласно модели измерений задачи, если бы фазовый вектор, в самом деле, принял значение . В результате применения к априорным оценкам соотношений коррекции оценка фазового вектора системы несколько уточнится и примет значение , что позволит более точно (по крайней мере, в окрестности момента времени ) прогнозировать поведение фазового вектора исследуемой динамической системы с помощью модели движения задачи.

В момент времени в качестве априорной оценки используется результат прогноза на траектории проходящей через фазовый вектор , снова строится разность измерений по которой вычисляется апостериорное, еще более точное значение и т.д. до тех пор, пока есть векторы измерений для обработки или есть необходимость прогнозировать поведение фазового вектора.