Нелинейное звено, охваченное обратной связью

Пусть входной случайный сигнал является гауссовским. В результате преобразования входного сигнала нелинейным звеном выходной сигнал уже не сможет оставаться гауссовским. А в случае если нелинейное звено, подлежащее статистической линеаризации, охвачено обратной связью, в формирование сигнала на входе в нелинейное звено вносит вклад не только входной гауссовский сигнал системы , но и выходной негауссовский сигнал .

В результате линеаризации звена возникнет ситуация, когда статистические характеристики сигнала на входе в нелинейное звено зависят в т.ч. и от результатов линеаризации.

Структурная схема системы, полученной в результате линеаризации, приобретет вид, изображенный на рисунке.

Для наглядности перерисуем схему так, чтобы выходным сигналом стал сигнал (вход в нелинейное звено).

Статистические характеристики выходного сигнала, необходимые для построения значений коэффициентов линеаризации, могут быть построены на основе использования следующих соотношений (см. раздел «Прохождение случайного сигнала через линейную систему»):

;
,

где:

– частотная характеристика системы с учетом результатов линеаризации;
и – математическое ожидание и спектральная плотность входного сигнала системы .

В общем случае, когда на систему воздействует более одного случайного процесса , а система содержит более одного нелинейного звена с входными сигналами 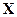, необходимо построить множество передаточных функций от каждого входа к каждому выходу системы .

Окончательные соотношения для вычисления статистических характеристик сигналов 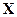имеют вид:

;
.

Дисперсии компонент вектора 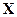могут быть вычислены при помощи интегрирования в бесконечных пределах по диагональных элементов матрицы :

.

Моделирование случайных процессов

Моделирование случайного процесса с заданными наперед математическим ожиданием и корреляционной функцией (или соответствующей ей спектральной плотностью ) выполняется на основе преобразования белого шума (с постоянной спектральной плотностью ) линейным динамическим звеном, именуемым формирующим фильтром, с передаточной функцией , подлежащей определению из соотношения:

.

Формирующий фильтр

Как правило, параметры определяется путем приравнивания коэффициентов полиномов числителя и знаменателя в уравнении

при одинаковых степенях .

После определения передаточной функции формирующего фильтра результирующая схема моделирования случайного процесса выглядит, как показано на рисунке.

Например, спектральная плотность процесса , подлежащего моделированию имеет вид:

,

математическое ожидание , а для моделирования используется белый шум с интенсивностью , следовательно, обладающий единичной спектральной плотностью.

Очевидно, что числитель и знаменатель искомой передаточной функций должны иметь порядки 1 и 2 (в самом деле, будучи возведенной в квадрат по модулю передаточная функция образует частное полиномов 2-й и 4-й степеней)

Т.о. передаточная функция формирующего фильтра в наиболее общем виде выглядит следующим образом:

,

а квадрат ее модуля:

.

Приравняем полученные соотношения:

.

Вынесем за скобку и в правой части равенства, приравнивая тем самым коэффициенты при нулевых степенях :

,

откуда с очевидностью вытекают следующие равенства:

; ; ; .

Т.о. структурная схема формирования случайного процесса с заданными статистическими характеристиками из белого шума с единичной спектральной плотностью выглядит, как показано на рисунке, с учетом рассчитанных значений параметров формирующего фильтра.

Моделирование белого шума

Для моделирования случайного процесса с заданными статистическими характеристиками в качестве входного случайного процесса в формирующий фильтр используется белый шум. Однако, точное моделирование белого шума нереализуемо из-за бесконечной дисперсии этого случайного процесса.

По этой причине, в качестве замены белому шуму, воздействующему на динамическую систему, используется случайный ступенчатый процесс. Интервал, на котором реализация случайного процесса сохраняет свое значение неизменной (ширина ступеньки, интервал корреляции), – величина постоянная. Сами значения реализации (высоты ступенек) – случайные величины, распределенные по нормальному закону с нулевым математическим ожиданием и ограниченной дисперсией. Значения параметров процесса – интервал корреляции и дисперсия – определяются характеристиками динамической системы, на которую оказывает воздействие белый шум.

Идея метода основывается на ограниченности полосы пропускания любой реальной динамической системы. Т.е. коэффициент усиления реальной динамической системы уменьшается по мере увеличения частоты входного сигнала, а, следовательно, существует такая частота (меньше бесконечной), для которой коэффициент усиления системы столь мал, что можно положить его нулевым. А это, в свою очередь, означает, что входной сигнал с постоянной, но ограниченной этой частотой, спектральной плотностью, для такой системы будет эквивалентен белому шуму (с постоянной и бесконечной спектральной плотностью).

Параметры эквивалентного случайного процесса – интервал корреляции и дисперсия вычисляются следующим образом:

; ,

где – эмпирически определяемая граница полосы пропускания динамической системы.