Априорный анализ динамических систем

Оглавление

Оглавление 2

Введение 4

Априорный анализ динамических систем 5

Прохождение случайного сигнала через линейную систему 5

Эволюция фазового вектора системы 7

Эволюция ковариационной матрицы фазового вектора системы 8

Статистическая линеаризация 8

Первый способ 9

Второй способ 10

Вычисление коэффициентов линеаризации 10

Неоднозначность в нелинейных звеньях 14

Нелинейное звено, охваченное обратной связью 15

Моделирование случайных процессов 16

Формирующий фильтр 16

Моделирование белого шума 17

Оценивание статистических характеристик динамических систем методом Монте-Карло 18

Точность оценок 18

Нестационарные динамические системы 20

Стационарные динамические системы 21

Апостериорный анализ динамических систем 22

Фильтр Калмана 22

Модель движения 22

Модель измерений 23

Коррекция 23

Прогноз 23

Оценивание 23

Использование калмановской фильтрации в нелинейных задачах 25

Метод наименьших квадратов 27

Построение оценок 27

Прогноз 29

Использование метода наименьших квадратов в нелинейных задачах 29

Построение матрицы Коши 30

Моделирование измерений 30

Численные методы 31

Специальные функции 31

Моделирование случайных величин 31

Равномерно распределенные случайные величины 31

Гауссовские случайные величины 32

Случайные векторы 33

Интеграл вероятностей 34

Полиномы Чебышева 36

Интегрирование обыкновенных дифференциальных уравнений 36

Методы Рунге-Кутты 36

Точность результатов численного интегрирования 37

Вложенный метод Дормана-Принса 5(4) порядка 37

Многошаговые методы 39

Методы Адамса 39

Интегрирование уравнений с запаздывающим аргументом 40

Сравнение вычислительных качеств методов 40

Задача Аренсторфа 40

Эллиптические функции Якоби 41

Задача двух тел 41

Уравнение Ван-дер-Поля 42

«Брюсселятор» 42

Уравнение Лагранжа для висячей струны 42

«Плеяды» 42

Оформление пояснительной записки 43

Титульный лист 43

Раздел «Оглавление» 44

Раздел «Введение» 44

Раздел «Теория» 44

Раздел «Алгоритм» 44

Раздел «Программа» 45

Раздел «Результаты» 45

Раздел «Выводы» 45

Раздел «Список использованных источников» 45

Приложения 45

Литература 47

Введение

В настоящем учебном пособии содержатся методические указания к выполнению заданий курсовых проектов и к проведению практических занятий по курсу «Основы статистической динамики».

Целью курсового проектирования и практических занятий является овладение студентами технологией априорного и апостериорного анализа нелинейных динамических систем, находящихся под воздействием случайных возмущений.

Априорный анализ динамических систем

Статистическая линеаризация

Статистическая линеаризация позволяет преобразовать исходную нелинейную динамическую систему т.о., чтобы для ее анализа удалось воспользоваться методами, алгоритмами, соотношениями, справедливыми для линейных систем.

Настоящий раздел посвящен изложению метода статистической линеаризации, основывающемуся на наиболее простом приближенном подходе, предложенным проф. И.Е. Казаковым, позволяющем, тем не менее, построить оценки точности системы, содержащей даже существенные нелинейности с разрывными характеристиками.

Статистическая линеаризация состоит в замене исходной безынерционной нелинейной зависимости между входным и выходным процессами такой приближенной зависимостью , линейной относительно центрированного входного случайного процесса , которая является эквивалентной в статистическом смысле по отношению к исходной:

Звено, обладающее такой приближенной зависимостью между входным и выходным сигналами, называется эквивалентным рассматриваемому нелинейному звену .

Величина выбирается исходя из условия равенства математических ожиданий нелинейного и линеаризованного сигналов и носит название статистической средней характеристики эквивалентного звена:

,

где – плотность распределения входного сигнала .

Для нелинейных звеньев с нечетными характеристиками, т.е. при , статистическую характеристику удобно представить в виде:

,

где:

– математическое ожидание входного сигнала ;
– статистический коэффициент усиления эквивалентного звена по средней составляющей .

Т.о. эквивалентная зависимость в данном случае приобретает вид:

.

Характеристику называют статистическим коэффициентом усиления эквивалентного звена по случайной составляющей (флуктуациям) и определяют двумя способами.

Первый способ

В соответствии с первым способом статистической линеаризации коэффициент выбирается исходя из условия равенства дисперсий исходного и эквивалентного сигналов. Т.о. для вычисления получим следующее соотношение:

,

где – дисперсия входного случайного воздействия.

Знак в выражении для определяется характером зависимости в окрестности значения аргумента . Если возрастает, то , а если убывает, то .

Второй способ

Значение по второму способу выбирается из условия минимизации средней квадратической ошибки линеаризации:

, где .

Окончательное соотношение для вычисления коэффициента по второму способу имеет вид:

.

В заключение заметим, что ни один их двух, рассмотренных выше, способов линеаризации не обеспечивает равенства корреляционных функций выходных сигналов нелинейного и эквивалентного звеньев. Расчеты показывают, что для корреляционной функции нелинейного сигнала первый способ выбора дает оценку сверху, а второй способ – оценку снизу, т.е. ошибки в определении корреляционной функции нелинейного выходного сигнала имеют разные знаки. Проф. И.Е. Казаков, автор, изложенного здесь метода, рекомендует выбирать в качестве результирующего коэффициента линеаризации полусумму коэффициентов , полученных по первому и второму способам.

Формирующий фильтр

Как правило, параметры определяется путем приравнивания коэффициентов полиномов числителя и знаменателя в уравнении

при одинаковых степенях .

После определения передаточной функции формирующего фильтра результирующая схема моделирования случайного процесса выглядит, как показано на рисунке.

Например, спектральная плотность процесса , подлежащего моделированию имеет вид:

,

математическое ожидание , а для моделирования используется белый шум с интенсивностью , следовательно, обладающий единичной спектральной плотностью.

Очевидно, что числитель и знаменатель искомой передаточной функций должны иметь порядки 1 и 2 (в самом деле, будучи возведенной в квадрат по модулю передаточная функция образует частное полиномов 2-й и 4-й степеней)

Т.о. передаточная функция формирующего фильтра в наиболее общем виде выглядит следующим образом:

,

а квадрат ее модуля:

.

Приравняем полученные соотношения:

.

Вынесем за скобку и в правой части равенства, приравнивая тем самым коэффициенты при нулевых степенях :

,

откуда с очевидностью вытекают следующие равенства:

; ; ; .

Т.о. структурная схема формирования случайного процесса с заданными статистическими характеристиками из белого шума с единичной спектральной плотностью выглядит, как показано на рисунке, с учетом рассчитанных значений параметров формирующего фильтра.

Моделирование белого шума

Для моделирования случайного процесса с заданными статистическими характеристиками в качестве входного случайного процесса в формирующий фильтр используется белый шум. Однако, точное моделирование белого шума нереализуемо из-за бесконечной дисперсии этого случайного процесса.

По этой причине, в качестве замены белому шуму, воздействующему на динамическую систему, используется случайный ступенчатый процесс. Интервал, на котором реализация случайного процесса сохраняет свое значение неизменной (ширина ступеньки, интервал корреляции), – величина постоянная. Сами значения реализации (высоты ступенек) – случайные величины, распределенные по нормальному закону с нулевым математическим ожиданием и ограниченной дисперсией. Значения параметров процесса – интервал корреляции и дисперсия – определяются характеристиками динамической системы, на которую оказывает воздействие белый шум.

Идея метода основывается на ограниченности полосы пропускания любой реальной динамической системы. Т.е. коэффициент усиления реальной динамической системы уменьшается по мере увеличения частоты входного сигнала, а, следовательно, существует такая частота (меньше бесконечной), для которой коэффициент усиления системы столь мал, что можно положить его нулевым. А это, в свою очередь, означает, что входной сигнал с постоянной, но ограниченной этой частотой, спектральной плотностью, для такой системы будет эквивалентен белому шуму (с постоянной и бесконечной спектральной плотностью).

Параметры эквивалентного случайного процесса – интервал корреляции и дисперсия вычисляются следующим образом:

; ,

где – эмпирически определяемая граница полосы пропускания динамической системы.

Точность оценок

Оценки математического ожидания

и дисперсии

случайной величины , построенные на основе обработки ограниченной выборки ее реализаций , , сами являются случайными величинами.

Очевидно, что чем больше размер выборки реализаций, тем точнее несмещенная оценка, тем ближе она к истинному значению оцениваемого параметра. Ниже приведены приближенные формулы, основывающиеся на предположении об их нормальном распределении[1]. Симметричный относительно доверительный интервал для оценки , соответствующий доверительной вероятности , определяется величиной , для которой справедливо соотношение:

,

где
– истинное значение математического ожидания случайной величины ,
– среднеквадратическое отклонение случайной величины ,
– интеграл вероятностей.

На основе приведенного выше соотношения величина может быть определена следующим образом:

,

где – функция, обратная по отношению к интегралу вероятностей .

Поскольку характеристика рассеивания оценки нам в точности не известна, воспользуемся ее ориентировочным значением, вычисленным с использованием оценки :

.

Т.о. окончательное соотношение, связывающие точность оценки математического ожидания и размера выборки, по которой производится оценивание, выглядит следующим образом:

.

Это означает, что величина доверительного интервала (при неизменном значении доверительной вероятности ), расположенного симметрично относительно , выраженная в долях оценки среднеквадратического отклонения , обратно пропорциональна квадратному корню из размера выборки .

Доверительный интервал для оценки дисперсии определяется аналогичным образом:

с точностью до величины , которая за неимением более точной информации может быть приблизительно определена из соотношения:

.

Т.о. величина доверительного интервала (при неизменном значении доверительной вероятности ), расположенного симметрично относительно , выраженная в ее долях, обратно пропорциональна квадратному корню из величины , где – размер выборки.

Более точные формулы для построения доверительных интервалов[2] оценок могут быть получены с использованием точных сведений о законе распределения случайной величины .

Например, для гауссовского закона распределения случайная величина

подчиняется закону распределения Стъюдента с степенью свободы, а случайная величина

распределена по закону также с степенью свободы.

Фильтр Калмана

Модель движения

Как известно, Фильтр Калмана предназначен для оценивания вектора состояния 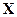линейной динамической системы, модель эволюции которого может быть записана в виде:

,

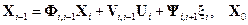где
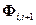– матрица Коши[6], определяющая изменение вектора состояния системы в ее собственном движении (без управляющих и шумовых воздействий) от момента времени 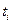к моменту времени ;
– вектор вынуждающих неслучайных воздействий на систему (например, управляющих воздействий) в момент времени ;
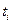– матрица влияния вынуждающих воздействий в момент времени 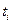на вектор состояния системы в момент времени ;
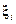– вектор случайных независимых центрированных воздействий на систему в момент времени ;
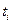– матрица влияния случайных воздействий в момент времени 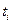на вектор состояния системы в момент времени .

Модель измерений

Оценивание выполняется на основе статистической обработки результатов измерений 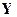, линейно связанных с вектором состояния 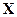, и искаженных аддитивной несмещенной ошибкой :

,

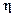где 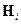– матрица, связывающая векторы состояния и измерений в один и тот же момент времени .

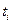Коррекция

Основу Фильтра Калмана составляют соотношения коррекции, являющиеся результатом минимизации следа ковариационной матрицы апостериорной плотности распределения линейной (по вектору измерений ) оценки вектора состояния системы :

где – ковариационная матрица вектора .

Прогноз

Дополняя соотношения коррекции соотношениями прогноза, основанными на линейных свойствах модели эволюции системы:

где – ковариационная матрица вектора 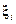, получим формулы рекуррентного байесовского алгоритма оценивания вектора состояния системы 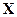и его ковариационной матрицы на основе статистической обработки результатов измерений .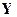

Оценивание

Очевидно, для реализации приведенных соотношений необходимо уметь строить матрицы 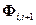, из модели эволюции, матрицу 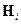из модели измерений, а также ковариационные матрицы и для каждого 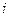-го момента времени.

Кроме того, для инициализации вычислительного процесса необходимо каким-либо образом определить апостериорные , или априорные , оценки вектора состояния и его ковариационной матрицы. Термин «априорные» или «апостериорные» в данном случае означает лишь то качество, в котором вектор состояния и его ковариационная матрица будут использованы в вычислительном алгоритме, и не говорит ничего о том, каким образом они были получены.

Таким образом, выбор соотношения, с которого следует начинать вычисления, определяется тем, к каким моментам времени отнесены начальные условия фильтраци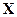и и и первый необработанный вектор измерений 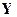. Если моменты времени совпадают, то первым следует применить соотношения коррекции, позволяющие уточнить начальные условия, если нет, то сначала следует спрогнозировать начальные условия к моменту привязки первого необработанного вектора измерений.

Поясним алгоритм калмановской фильтрации при помощи рисунка.

На рисунке в осях координат 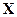, 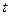(в канале движения) изображены несколько возможных траекторий фазового вектора :

– истинная траектория эволюции фазового вектора;
– эволюция фазового вектора, прогнозируемая на основе использования модели движения и априорной оценки фазового вектора , отнесенной к моменту времени ;
– эволюция фазового вектора, прогнозируемая на основе использования модели движения и апостериорной (более точной) оценки фазового вектора , отнесенной к моменту времени

В осях координат 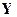, 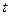(в канале измерений) в моменты времени и изображены результаты измерений и :

,

где
– истинное значение вектора измерений в момент времени ;
– вектор ошибок измерений, реализовавшихся в момент времени .

Для построения поправки к априорному фазовому вектору системы используется разность между результатом измерения и тем значением, которое было бы измерено согласно модели измерений задачи, если бы фазовый вектор, в самом деле, принял значение . В результате применения к априорным оценкам соотношений коррекции оценка фазового вектора системы несколько уточнится и примет значение , что позволит более точно (по крайней мере, в окрестности момента времени ) прогнозировать поведение фазового вектора исследуемой динамической системы с помощью модели движения задачи.

В момент времени в качестве априорной оценки используется результат прогноза на траектории проходящей через фазовый вектор , снова строится разность измерений по которой вычисляется апостериорное, еще более точное значение и т.д. до тех пор, пока есть векторы измерений для обработки или есть необходимость прогнозировать поведение фазового вектора.

Метод наименьших квадратов

В настоящем разделе представлен метод наименьших квадратов, адаптированный для апостериорного анализа динамических систем.

Построение оценок

Для случая линейной модели равноточных измерений:

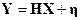
имеем следующий алгоритм оценивания фазового вектора:

.

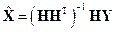Для случая неравноточных измерений вводится в рассмотрение матрица 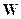, содержащая на диагонали весовые коэффициенты. С учетом весовых коэффициентов предыдущее соотношение примет вид:

.

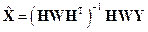Если в качестве весовой использовать матрицу, обратную к ковариационной матрице ошибок измерений 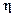, то с учетом того обстоятельства, что 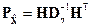получим:

.

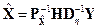Как следует из приведенных выше соотношений, основу метода составляет матрица 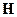, связывающая оцениваемый фазовый вектор 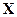, отнесенный к некоторому моменту времени 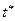, и вектор измерений 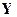. Вектор 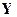имеет, как правило, блочную структуру, в которой каждый из блоков отнесен к некоторому моменту времени 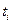, не совпадающую в общем случае с .

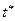На рисунке показано некоторое возможное взаимное расположение моментов времени, к которым отнесены измерения и момента времени, к которому отнесен вектор оцениваемых параметров.

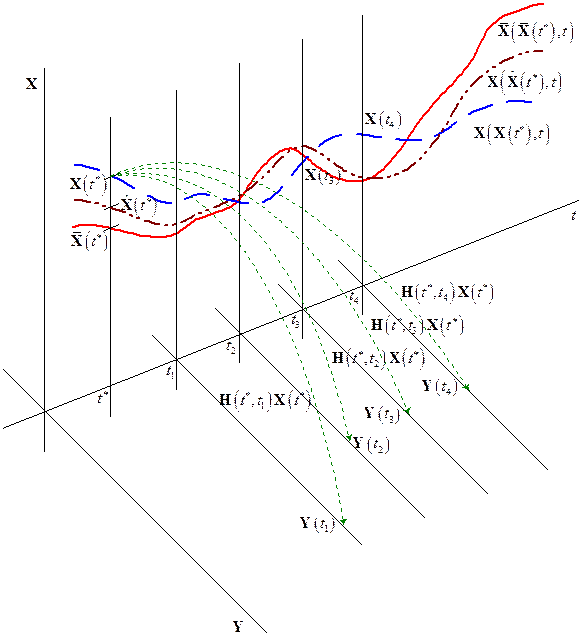
Для каждого вектора 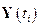справедливо следующее соотношение:

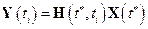, при .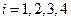

Таким образом, в результирующем соотношении метода наименьших квадратов вектор 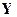и матрица 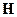имеют следующую структуру:

; .

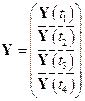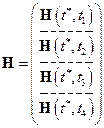Каждый блок матрицы 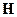может быть построен как результат произведения матрицы Коши, определяющей переход для фазового вектора системы от момента времени 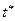к моменту 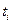, и матрицы, связывающей фазовый вектор и блок вектора измерений, отнесенные к одному и тому же моменту времени :

.

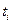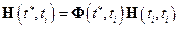Предпочтительным, с точки зрения обеспечения максимальной точности оценивания, является размещение момента времени, к которому привязан вектор оцениваемых параметров, в непосредственной близости от моментов, к которым привязаны измерения.

Прогноз

Для прогнозирования значения фазового вектора линейной системы

,

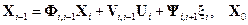где
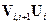– определяет неслучайное вынуждающее воздействие на систему;
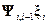– определяет случайное воздействие на систему.

могут быть использованы соотношения прогноза, встречавшиеся выше при описании алгоритма калмановской фильтрации:

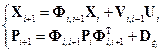
где 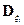– ковариационная матрица вектора .

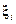Построение матрицы Коши

В задачах построения оценок методами статистической обработки измерений часто встречается задача построения матрицы Коши. Эта матрица связывает фазовые векторы системы, отнесенные к разным моментам времени, в собственном движении.

Ограничимся в настоящем разделе рассмотрением вопросов, связанных с построением матрицы Коши для модели эволюции, записанной в виде системы обыкновенных дифференциальных уравнений (линейных или нелинейных).

Для линейной системы имеем:

.

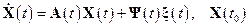Тогда дифференциальное уравнение для матрицы Коши примет вид:

.

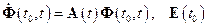Интегрируя его на интервале времени от 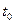до 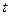, с единичной матрицей соответствующей размерности в качестве начальных условий, получим матрицу Коши, связывающую фазовые векторы, отнесенные к моментам времен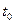и и :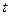

.

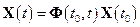В случае, когда модель эволюции фазового вектора представлена нелинейной системой дифференциальных уравнений общего вида:

,

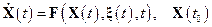матрица Коши может быть построена с использованием приведенных выше соотношений для линеаризованной системы:

,

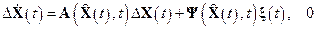где использованы следующие обозначения для матриц пропорциональности, построенных в окрестности опорной траектории , :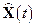

; .

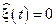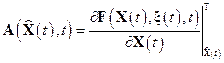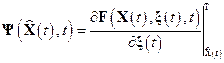Моделирование измерений

Проблема возникает в случае, когда, например, оценивая потенциально достижимую точность метода в некоторой задаче, Вы не располагаете какими-либо результатами измерениями. В этом случае результаты измерений требуется смоделировать. Особенность моделирования результатов измерений состоит в том, что модели движения и измерений, используемые для этой цели могут не совпадать с теми моделями, которые Вы будете использовать в ходе построения оценок с использованием того или иного метода фильтрации.

Более того, рекомендуется, чтобы модели, используемые для построения результатов измерений, были максимально точными, наилучшим образом приближенными к физическим процессам и закономерностям, наблюдающимся в природе.

В качестве начальных условий для моделирования эволюции фазового вектора динамической системы должны использоваться истинные значения координат этого вектора. Кроме этого места истинные значения координат фазового вектора системы не должны использоваться более нигде[7].

Численные методы

Специальные функции

Случайные векторы

Проблема, решение которой описано в настоящем подразделе, состоит в моделировании вектора коррелированных между собой гауссовских случайных величин.

Пусть случайный вектор 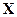, подлежащий моделированию, формируется на основе преобразования вектора стандартных некоррелированных случайных величин соответствующей размерности следующим образом:

,

где
– вектор математического ожидания ;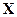
– матрица коэффициентов, подлежащих определению.

Как известно, ковариационная матрица вектора 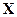, отвечающего приведенной выше зависимости, может быть определена на основе следующего соотношения:

.

Пусть матрица имеет вид:

.

Тогда, приравнивая левую и правую части уравнения поэлементно, для каждого из, например, нижнего треугольника, получим совокупность уравнений вида:

Разрешая полученные уравнения относительно элементов матрицы , получим окончательные соотношения:

Т.о. для получения вектора коррелированных случайных величин необходимо вычислить элементы матрицы в соответствии с приведенными выше формулами и сгенерировать реализации элементов вектора гауссовских случайных некоррелированных величин , после чего воспользоваться исходным соотношением подраздела.

Интеграл вероятностей

Вычисление значений коэффициентов статистической линеаризации основывается на использовании интеграла вероятностей:

.

Быстрый алгоритм вычисления данной функции для положительных с точностью до 4 знаков основывается на разложении в ряды по степеням аргумента для трех его интервалов.

На интервале значений аргумента вычисление интеграла вероятностей основывается на использовании экономизированного ряда:

.

На интервале – с помощью ряда Тейлора:

; ; .

Значение (верхний предел суммирования) определяется из условия:

.

На интервале – с помощью асимптотического ряда, вычисляемого с точностью до :

.

При сумма асимптотического ряда становится практически равной 1.

Расче<