Численное решение оптимизационных задач
Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют определить наилучший вариант конструкции, наилучшее распределение ресурсов, минимальный урон природной среде и т. п. В процессе решения задачи оптимизации необходимо найти оптимальные значения некоторых параметров (их называют проектными). Выбор оптимального решения проводится с помощью некоторой функции, называемой целевой. Целевую функцию можно записать в виде
, (3.10)
где х1, х2, … , хп – проектные параметры.
Можно выделить 2 типа задач оптимизации – безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума функции (3.10) от п действительных переменных и определении соответствующих значений аргументов на некотором множестве G n-мерного пространства. Обычно рассматриваются задачи минимизации; к ним легко сводятся и задачи на поиск максимума путем замены знака целевой функции на противоположный. Условные задачи оптимизации – это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве G.
Для поиска экстремумов в MathCad имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
- Minimize (f, xi, ... ,хм) - вектор значений аргументов, при которых функция f достигает минимума;
- Maximize (f, xi,... ,хм) - вектор значений аргументов, при которых функция f достигает максимума; f(xi,...,хм,...)-функция; xi, ...,хм- аргументы, по которым производится минимизация(максимизация). Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения
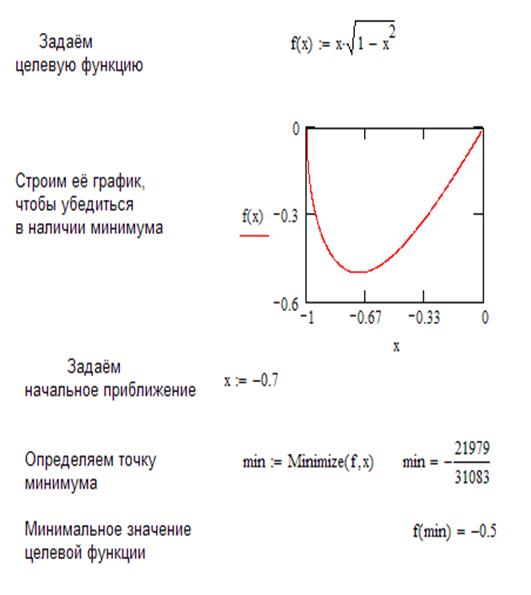
Пример . Найти координату и минимальное значение функции одной переменной
на отрезке [-1.0; 0.0]
Текст документа MathCAD
Пример. Найти и вывести на печать координаты и минимальное значение функции двух переменных при погрешностях 10-2, 10-20 функции двух переменных f(x, y) =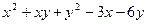 
, если начальная точка поиска имеет координаты М0 (0.5; .5).
Текст документа MathCAD
погрешность= 10-2
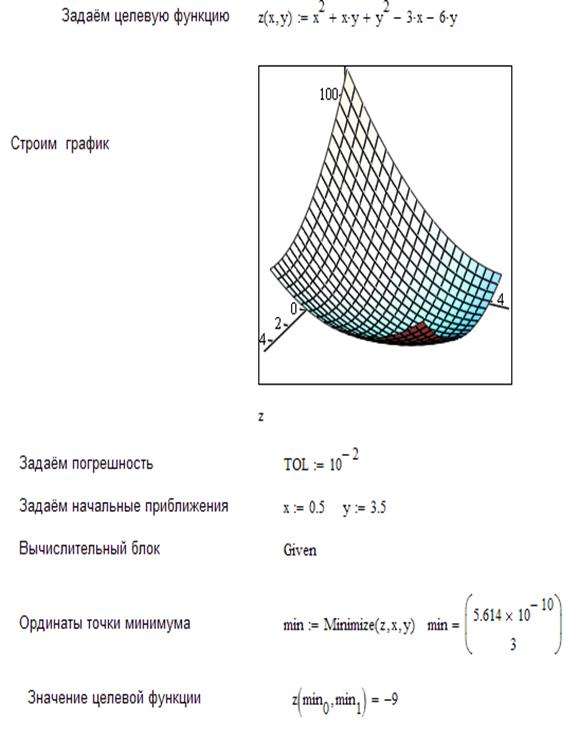
погрешность= 10-20
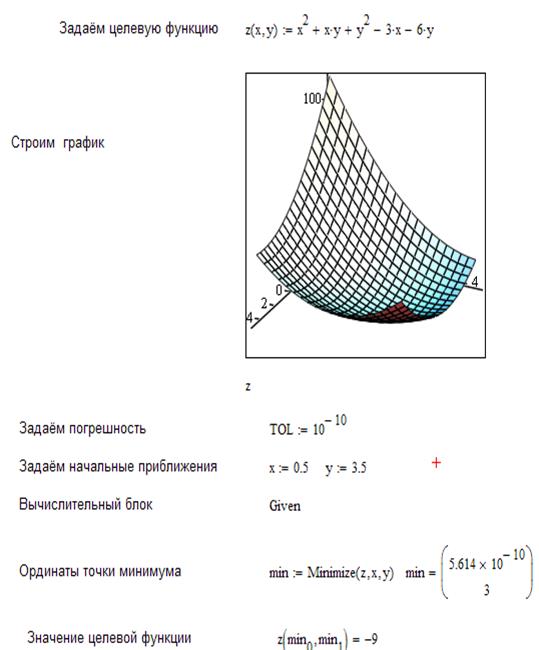
Вывод:Я научился решать оптимизационные задачи 2-х типов: безусловные и условные
Общий вывод:Янаучился пользоваться простейшими методами вычислений в математической системе MathCAD, которая является одной из самых мощных и эффективных математических систем.В процессе выполнения работы я заметил, что MathCAD остается единственной системой, в которой описание решия математических задач задается с помощью привычных математических формул и знаков. MathCAD позволяет выполнять как численные, так и аналитические (символьные) вычисления, имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства научной графики.
Литература
1. Mathcad 6.0 Plus. Финансовые, инженерные и научные расчеты в среде Windows 95./Перевод с англ. - М.: Информационно-издательский дом “Филинъ”, 1996. -712 с.
2. Дьяконов В.П. Справочник по MathCAD PLUS 6.0 PRO. - М.: “СК Пресс”, 1997. - 336 с.: ил.
3. Дьяконов В.П., Абраменкова И.В. MathCAD 8 PRO в математике, физике и Internet. - М.: “Нолидж”, 2000. - 512 с.: ил.
4. Кудрявцев Е.М. MathCAD 2000 Pro. – М.: ДМК Пресс, 2001. – 576 с.: ил.
5. Очков В. Ф. Mathcad 7 Pro для студентов и инженеров. - М.: КомпьютерПресс, 1998. - 384 с.: ил.
6. Плис А.И., Сливина Н.А. Mathcad 2000. Лабораторный практикум по высшей математике. - М.: Высш. шк., 2000. - 716 с.: ил.