Тема 3. Нахождение обратных матриц. Решение матричных уравнений.

Краткие теоретические сведения

Определение. Квадратная матрица, определитель которой отличен от 0, называется невырожденной. Квадратная матрица, определитель которой равен 0, называется вырожденной.

Свойство 1. Вырожденная матрица не обратима.

Свойство 2. Произведение невырожденных матриц есть невырожденная матрица.

Свойство 3. Для каждой невырожденной квадратной матрицы А порядка n существует квадратная матрица А^-1, такая что А´А^-1= А^-1´А =Е, где Е – единичная матрица.

Определение. Квадратная матрица А^-1, такая что А´А^-1= А^-1´А =Е, где Е – единичная матрица, называемая обратной матрице А.

Основные свойства обратной матрицы.

1. (А^-1)^-1=А
2. (А^-1)¢=(А¢)^-1
3. (А´В)^-1=В^-1´А^-1
4. 
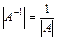
5. Е^-1=Е

Основные алгоритмы вычисления обратной матрицы.

Алгоритм №1 вычисления обратной матрицы:

1. Вычислить определитель матрицы ½A½=D;

2. Найти алгебраические дополнения ко всем элементам матрицы;

3. Все элементы матрицы заменить их алгебраическими дополнениями;

4. Транспонировать полученную матрицу;

5. Разделить все элементы матрицы на D;

6. Полученная на этапе 5 матрица и есть матрица А^-1, обратная матрице А.

Определение. Под элементарными преобразованиями матриц понимаются следующие операции:

1. Умножение или деление строки (столбца) матрицы на число к¹0;

2. Прибавление строки (столбца), умноженной на некоторое число к¹0 к другой строке (столбцу); при этом изменяется та строка (столбец), к которой прибавляют, остальные строки (столбцы) не изменяются;

3. Перемена местами строк (столбцов).

Алгоритм №2 вычисления обратной матрицы:

1. Присоединить к матрице А за вертикальной чертой единичную матрицу Е того же порядка, что и А; получим новую матрицу (А|Е);
2. Применяя элементарные преобразования 1-3 над строками матрицы (А|Е) получить слева от вертикальной черты единичную матрицу Е;
3. Тогда справа от вертикальной черты получим матрицу А^-1, обратную к матрице А.

Матричные уравнения.

Определение. Матричным уравнением будем называть уравнение вида A´X=B, где А и В заданные матрицы, Х – неизвестная матрица.

Если матрица А невырожденная, тогда для нее существует обратная. Умножив обе части уравнения A´X=B на А^-1, получим

A^-1 ´ (A´X)=A^-1 ´BÞ (A^-1 ´A)´C=A^-1 ´B Þ C=A^-1 ´B

Покажем, что Х - решение уравнения A´X=B:

A´ (A^-1´B)= (A´A^-1) ´B=Е´В=В Û B=B.

Пример выполнения заданий практической части

Пример 1. Найти матрицу А^-1, обратную матрице .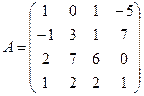

Решение.

1. Определитель матрицы А : .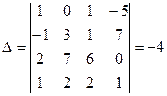

2. Найдем алгебраические дополнения ко всем элементам матрицы:

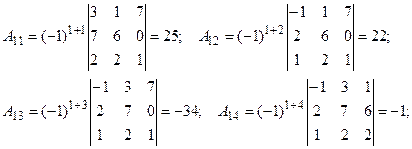
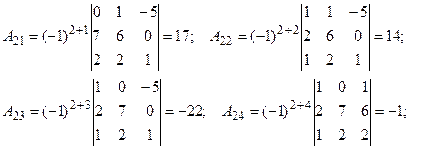
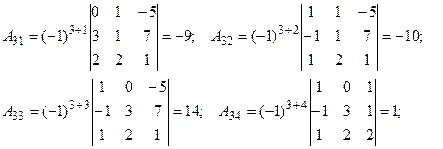
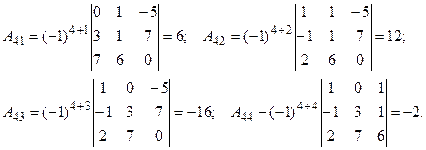
3. Составим матрицу, заменив все элементы матрицы А их алгебраическими дополнениями:

.

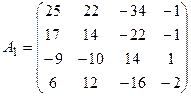4. Транспонируем полученную матрицу А₁: .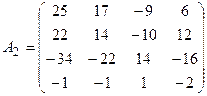

5. Разделим все элементы матрицы А₂ на значение определителя D=-4: .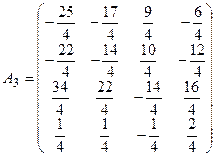

Таким образом, матрица, обратная матрице 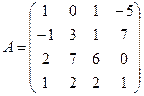, имеет вид: .

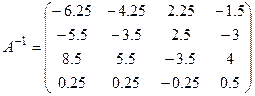Пример 2. Найти матрицу А^-1, обратную матрице .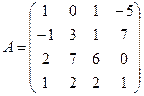

Решение.

1. Единичная матрица четвертого порядка имеет вид: 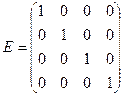. Составим присоединенную матрицу (А|Е): .

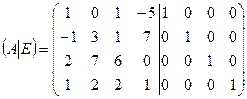2. С помощью элементарных преобразований получим слева от вертикальной черты единичную матрицу Е.

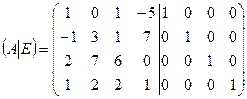=[ко второй строке прибавим первую]= = 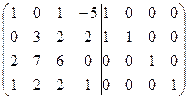=[вычтем из третьей строки первую, умноженную на 2]= = 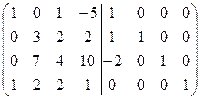=[вычтем из четвертой строки первую]= = 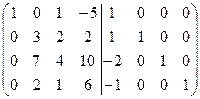=[вычтем из второй строки четвертую, для того чтобы получить во второй строке второй элемент равный 1]= = 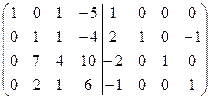=[вычтем из третьей строки вторую, умноженную на 7]= = 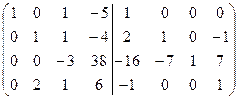=[вычтем из четвертой строки вторую, умноженную на 2]= 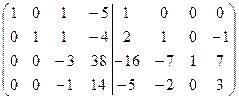=[вычтем из третьей строки четвертую, умноженную на 2]= 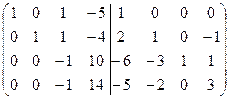=[разделим все элементы третьей строки на (-1)]= 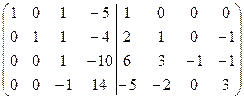=[прибавим к четвертой строке третью]= = 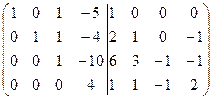=[разделим все элементы четвертой строки

на 4]= 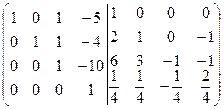=[к третьей строке прибавим четвертую, умноженную на 10]= 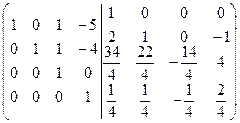=[ко второй строке прибавим четвертую, умноженную на 4]= 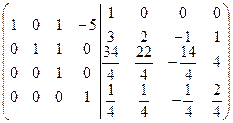=[к первой строке прибавим четвертую, умноженную на 5]= 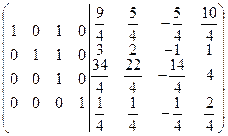=[из второй строки вычтем третью] = 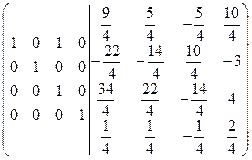=[из первой строки вычтем третью]= = .

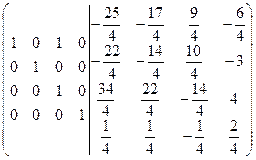Таким образом, матрица, обратная матрице А, имеет вид: или .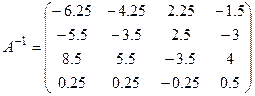

Пример 3. Решить матричные уравнения A´X=B, A´X´В=С, если

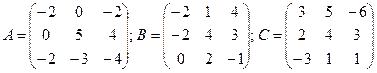
Решение.

1. Решим матричное уравнение .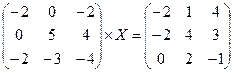

C=A^-1 ´B

1) Найдем матрицу А^-1. Воспользуемся первым способом.

DА=-4.

2)

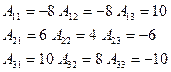
3) Составим матрицу из алгебраических дополнений к элементам матрицы А:

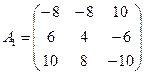
4) Транспонируем полученную матрицу: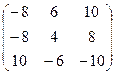

5) Разделим каждый элемент полученной матрицы на значение DА= - 4: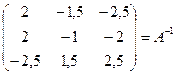

6)

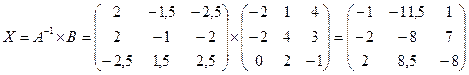
2. Решим матричное уравнение .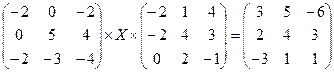

1) ;

;

;

;

.

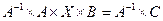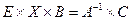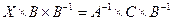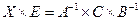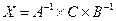2) Найдем матрицу, обратную к матрице В:

DВ=2

3)

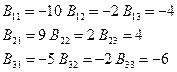
4) Составим матрицу из алгебраических дополнений к элементам матрицы В:

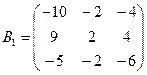
5) Транспонируем полученную матрицу: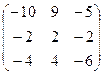

6) Разделим каждый элемент полученной матрицы на значение DВ=2: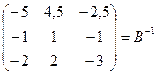

7)

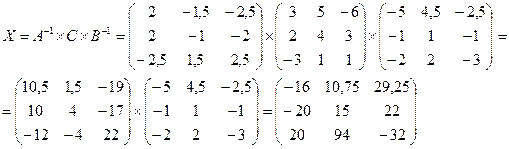
Ответ: ; .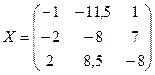

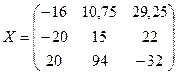Задания для аудиторного занятия

1. Убедиться, что каждая из следующих матриц обратима и найти к каждой матрице обратную:

1.1. 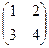; 1.2. 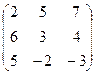; 1.3. ;

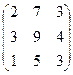1.4. ; 1.5. .

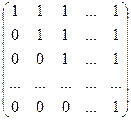2. Решить матричные уравнения 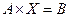и 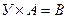, если:

2.1. ;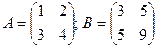

2.2. ;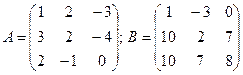

2.3. .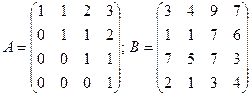

3. Решить матричные уравнения:

3.1. 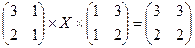; 3.2. ;

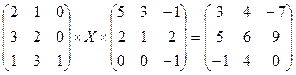3.3. .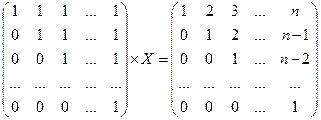

4. Пусть А и В – обратимые матрицы одного и того же порядка. Показать, что следующие равенства равносильны между собой:

€ ;

€ ;

€ ;

€ .

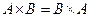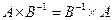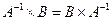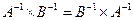3.4. Домашнее задание

1. Для каждой матрицы найти обратную.

1.1. 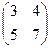; 1.2. 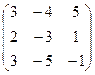; 1.3. ;

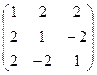1.4. 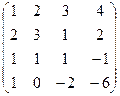; 1.5. .

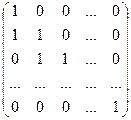2. Решить матричные уравнения 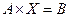и 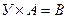, если:

2.1. 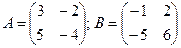; 2.2. .

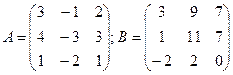3. Решить матричные уравнения:

3.1. ;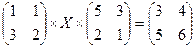

3.2. ;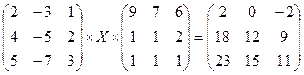

3.3. .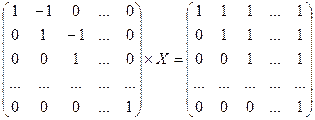

4. Определить, как изменится обратная матрица А^-1, если в данной матрице А:

4.1. переставить i-ую и g-ую строки;

4.2. все элементы i-ой строки умножить на число к¹0;

4.3. к i-ой строке прибавить g-ую строку, умноженную на число к¹0.

Тема 4. Ранг матрицы