Решение показательных уравнений.

Показательными уравнениями называют уравнения вида

где а — положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.

Решение показательных уравнений основано на теореме:

Теорема. Показательное уравнение 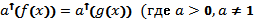) равносильно уравнениюf(x)=g(x) (в области определения обеих функций).

Решение показательных неравенств.

Показательными неравенствами называют неравенства вида:

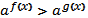
где а — положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.

Теорема. Показательное неравенство 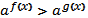равносильно неравенству того же смысла 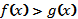, если 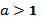(в области определения обеих функций).

Показательное неравенство 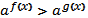равносильно неравенству того же смысла 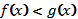если 0<a<1 (в области определения обеих функций).

Задания.

№ 1. Решить уравнения и неравенства графически:

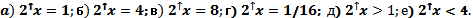
№ 2. Решить уравнение.

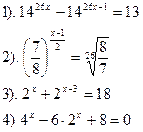
№ 3. Решить неравенство:

1. 
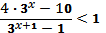
2. 0,4 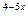< 0,16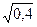
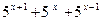3. > 31
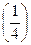
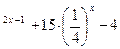4. . < 0

Занятие 11.

Тема занятия: «Логарифмическая функция. Логарифмические уравнения и неравенства.»

План занятия.

1. Знакомство с теоретическим материалом.
2. Разбор заданий под руководством преподавателя.
3. Самостоятельное выполнение заданий.

Методические материалы.

Понятие логарифма

Логарифмом числа b по основанию a (где a > 0, a ≠ 1) называют показатель степени, в которую надо возвести a, чтобы получить число b, обозначают символом log_ab.

Если a > 0, a ≠ 1, то log_a b по определению есть показатель степени, в которую надо возвести число a, чтобы получить число b. Поэтому равенствоa^log_a^b = b есть тождество, которое называют основным логарифмическим тождеством.

Десятичный логарифм lg b (по основанию 10), натуральный логарифм ln b (по основанию е).

Логарифмическая функция, ее свойства и график

1. Так как показательная функция y = a^x (где a > 0, a ≠ 1) является монотонной (возрастающей при a > 1 и убывающей при 0 < a < 1), то она имеет обратную функцию:

y=a^x, x=log_a y, y=log_a x. Функцию y = log_a x (где a > 0, a ≠ 1) называют логарифмической.

Итак, показательная и логарифмическая функции при одном и том же основании являются взаимно обратными функциями.

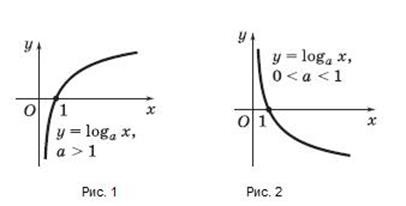
2. График логарифмической функции y = log_a x можно построить, воспользовавшись тем, что функция y = log_ax обратна показательной функции y = a^x. Поэтому достаточно построить график функции y = a^x, а затем отобразить его симметрично относительно прямой y = x. На рис. 1 изображен график функции y = log_a x при a > 1, а на рис. 2 — график фунции y = log_a x при 0 < a < 1.

3°. Отметим свойства функции y = log_a x при a > 1:

а) D(f) = R₊;

б) E(f) = R;

в) функция возрастает;

г) x = 1 ó loga x = 0;

д) 0 < x < 1 ó log_a x < 0;

е) x > 1 ó log_a x > 0.

4. Отметим свойства функции y = log_a x при 0 < a < 1:

а) D(f) = R₊;

б) E(f) = R;

в) функция убывает;

г) x = 1 ó log_a x = 0;

д) 0 < x < 1 ó log_a x > 0;

е) x > 1 ó log_a x < 0.

Свойства логарифмов

1. log_a N (где a > 0 и a ≠1) существует, если N > 0.

2. При основании a > 1 логарифмы чисел N > 1 положительны, а логарифмы чисел 0 < N < 1 отрицательны. Например, log₂ 5 > 0; log₃ 0,5 < 0.

3. При основании 0 < a < 1 логарифмы чисел N > 1 отрицательны, а логарифмы чисел 0<N<1 положительны. Например, log _0,5 5 < 0; log_0,51/3> 0.

4.Если N₁ = N₂, то log_a N₁ = log_a N₂.

5. Если a > 1 и если N₁ > N₂, то log_a N₁ > log_a N₂. Например, log ₃ 7 > log ₃ 5.

6. Если 0 < a < 1 и если N₁ > N₂, то log_a N₁ < log_a N₂. Например, log _1/3 9 < log _1/3 7.

7. log_a 1 = 0 (a > 0, a ≠ 1)

8. log_a a = 1.

9. log_a (N₁N₂ ... N_k) = log_a N₁ + log_a N₂ + ... + log_a N_k или log_a (N₁N₂) = log_a |N₁|+log_a |N₂|.

10. log_aN₁/N₂ = log_a N₁ – log_a N₂, если N₁>0, N₂>0. В общем случае log_aN₁/N₂=log_a |N₁|–log_a |N₂|.

11. log_a N^c = c log_a N; если N < 0, а c — четное число, то справедливо log_a N^c = c log_a │N│.

12. log_a N =log_acN^c ;log_a^k N = log_a N ^1/k = 1/k log_a N

Потенцирование

Потенцирование — это преобразование, обратное логарифмированию.

Логарифмические уравнения

Уравнение, содержащее переменную под знаком логарифма, называют логарифмическим. Простейшим примером логарифмического уравнения служит уравнение log_a x=b (где a>0, a≠1).

Решение логарифмического уравнения вида log_a f(x) = log_a g(x) основано на том, что такое уравнение равносильно уравнению f(x) = g(x) при дополнительных условиях f(x) > 0,g(x) > 0 (в области определения f(x) и g(x)).

Логарифмические неравенства

Неравенство, содержащее переменную под знаком логарифма, называют логарифмическим.

Неравенство log_a f(x) > log_a ϕ(x) равносильно системе f(x) > ϕ(x) > 0 при a?(1; +∞) и системе 0<f(x)<ϕ(x) при a ? (0; 1) (в области определения f(x) и g(x)).

Задания.

№ 1. Вычислить:

1. 25^1-(1/4)log₅⁴⁹ .
2. log₃₀ 8, если lg 5 = a и lg 3 = b

№ 2. Найдите область определения функции:

1. y = x + log _0,4 (5x + 4) – log₆ (8x + 7);
2. y = log₇ (x² – 3x) – log₄ x;
3. y = 3 lg (3 + 5x) – lg (4 + 9x)².

№ 3. Постройте график функции:

1. y =3^log₃^(-x) ; б) y = log₂ |x|;
2. y = log₂ log₂ x; г) y = |log₂ x|;

№ 4. Решить уравнение.

1. log 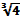(x – 1) = 6 4. log₃ (x² – 4x – 5) = log₃ (7 – 3x)
2. lg (x – 6) – 0,5 lg 2 = lg 3 + lg 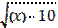5. log_x5 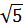– 1,25 = log²_x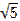
3. _x 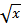= ( 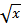)^x 6. x^log₂^x+2 = 8

Занятие 12.

Тема занятия: «Производная. Определение. Геометрический смысл. Производная сложной функции.»

План занятия.

1. Знакомство с теоретическим материалом.
2. Разбор заданий под руководством преподавателя.
3. Самостоятельное выполнение заданий.

Методические материалы.

Определение производной.

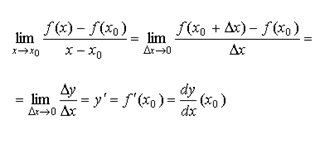Пусть f(x) - определена и непрерывна в окрестности x_0. Производная функции в точке x₀ и ее обозначения: