Статистическая обработка результатов эксперимента
В различных областях науки, при решении задач идентификации, оптимального управления и т.п., а также в процессе выполнения практических измерений зачастую необходимо не только определить погрешность измерения, но и дать оценку погрешности результатов эксперимента.
Например, для игнорирования грубых погрешностей необходима предварительная статистическая обработка результатов измерений, в общем случае рассматриваемых как случайные величины.
Случайным называется событие, которое при осуществлении определенного комплекса условий может либо произойти, либо не произойти.
Т.о. можно считать, что при проведении повторных наблюдений в одинаковых условиях каждая из множества возможных незначительных причин случайных изменений результатов может появиться или не появиться, может принимать любые значения как по величине, так и по знаку.
Для каждого i-го измерения Хi случайная абсолютная погрешность вычисляется по формуле D = Х - Хi, где X – истинное значение измеряемой величины.
Теоретически доказано, что если закон распределения случайной величины является нормальным (в большинстве случаев это так) и систематические погрешности полностью исключены, то истинное значение измеряемой величины равно математическому ожиданию результатов измерений. Математическое ожидание случайной величины - это такое ее значение, вокруг которого группируются результаты отдельных измерений или погрешностей. При ограниченном количестве N наблюдений их результаты характеризуют оценками параметров функции распределения случайной величины.
Оценкой математического ожидания M[Х] служит среднее арифметическое:
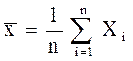
Мерой рассеяния значений случайной величины служит дисперсия D[x], оценка d которой выражается формулой
× 
.
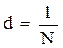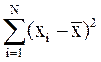Меру рассеяния также характеризуют среднеквадратическим отклонением S[x], оцениваемым величиной, равной G =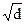 
. Оценку приписывают каждому из N результатов наблюдений и называют погрешностью единичного измерения, стандартным отклонением или стандартом.
Для проверки вида погрешности и отбрасывания аномальных наблюдений используют критерий
Vi =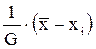 
Если, например, для N = 20 выполняется Vi > 2,71 (c вероятностью 0,025), то результат i-го измерения считается грубой погрешностью и отбрасывается как аномальный.
Мерой связи между двумя множествами {a} и {b} экспериментальных данных является коэффициент корреляции
r =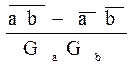 
Коэффициент корреляции может принимать значения от -1 до +1. Значение модуля коэффициента корреляции, равное 1, свидетельствует о функциональной зависимости между данными множеств, а нулевое его значение - о полной взаимной независимости элементов множеств.