Базовые структуры программирования
Выделяют три основные структуры алгоритмов:
1. Линейная.
2. Разветвляющаяся (альтернатива «если–то–иначе» или «если–то»).
3. Циклическая (повторение).
3. ЛИНЕЙНЫЕ СТРУКТУРЫ
Линейнаяструктура – является основной. Она означает, что действия выполняются друг за другом (рис. 2).
|
Присваивание переменной какого-либо значения или присваивание одной переменной значения другой переменной является наиболее часто выполняемым действием в программе, написанной на любом языке программирования. В языке программирования присваивание является операцией и обозначается как «:=». Это означает, что при выполнении этой операции происходит не только присваивание значения определенной переменной, но и возвращается некоторое значение. Оператор присваивания имеет вид А : = В.Сначала вычисляется выражение, представленное в правой части,причем все переменные, используемые в правой части, к моменту вычисления должны быть определены.Полученное значение присваиваетсяимени, записанному в левой части. Например, оператор присваивания S := S + Аiвыполняется следующим образом: к имеющемуся значению переменной S для заданного номераiэлемента последовательности {Ai}вычисляется сумма S + Аi,полученный результатснова записывается вячейку с именемS.Таким образом, происходит накапливание суммы. Аналогично оператор присваивания Р := Р * Аi осуществляет накапливание произведения. Однако в блок-схемах разрешается использовать знак «=».
Рассмотрим примеры линейных процессов.
Пример 1.По известным катетам прямоугольного треугольника определить радиусы вписанной и описанной окружностей, их площади, а также площадь данного треугольника. Реализовать алгоритм в виде блок-схемы.
Решение.
Расчетные формулы данной задачи имеют следующий вид. Пусть a, b - катеты прямоугольного треугольника, тогда гипотенуза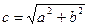 
, радиус описанной окружности 
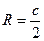, радиус вписанной окружности 
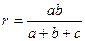, площади вписанной и описанной окружностей соответственно 
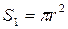и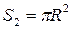 
, площадь данного треугольника 
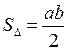. Последовательность действий (алгоритм) представим в виде блок-схемы.
 |
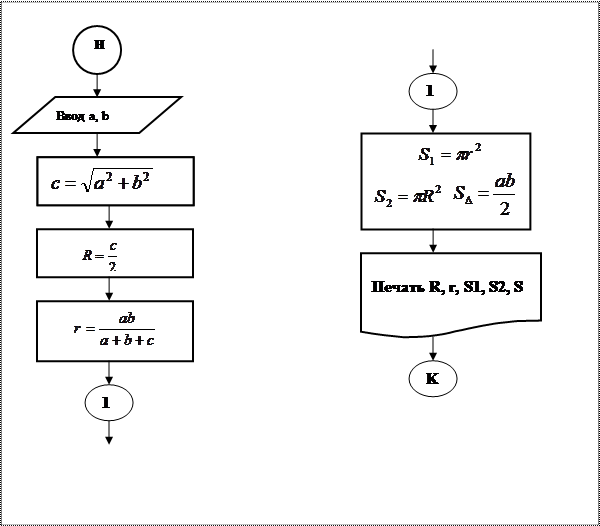Рис. 3. Блок-схема линейного процесса (задача 1)
|
Пример 2.
На судно производится погрузка контейнеров. Каждый контейнер имеет длину 3м., ширину 5м. и высоту 7м. Вес каждого контейнера 20 тонн. Сколько контейнеров можно погрузить в трюм размером 50*30*10 и каков общий вес груза?
Решение.
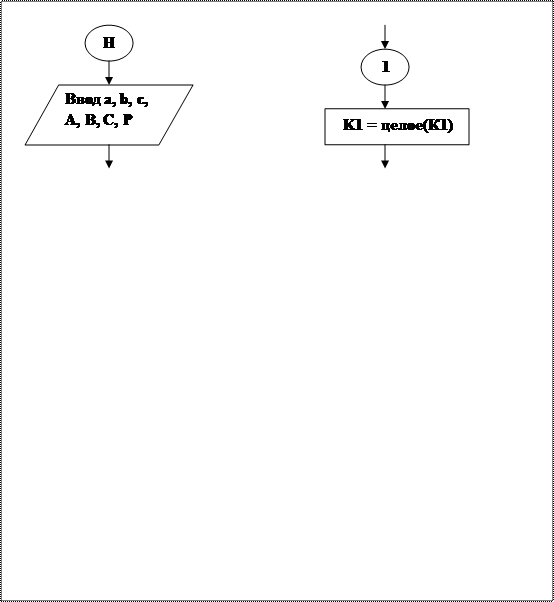
Сначала построим математическую модель поставленной задачи и разработаем последовательность действий (алгоритм). Итак, вычислим объем, занимаемый каждым контейнером: V = a·b·c.Далее,определим,какое максимальное количество контейнеров можно разместить по длине трюма (К1), по ширине (К2) и в высоту (К3). (Замечание: поскольку мы описываем линейный процесс, вопрос оптимизации размещения по длине и ширине не рассматривается!). Теперь подсчитаем общее количество погружаемых контейнеров и, наконец, общий вес груза.
Представим «словесный» алгоритм в виде блок-схемы. Чтобы можно было использовать этот алгоритм при любых размерностях контейнеров и трюма, введем обозначения: a –длина контейнера, b –ширина, c –высота, А – длина трюма, В –его ширина, С - высота, Р - вес одного контейнера.
Обратите внимание на то, что в блоках присваивания К1=целое(К1), К2=целое(К2), К3=целое(К3)влевой и правой части используется одно и то же имя переменной. Это означает, что сначала вычисляется оператор, стоящий в правой части, а полученное значение вносится в ячейку с именем левой части, т.е. изменяется содержимое ячейки.
|
|
 |  | ||
|
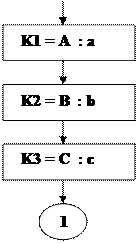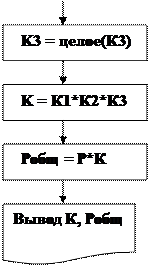СТРУКТУРЫ ВЕТВЛЕНИЯ
На практике часто встречаются задачи, в которых в зависимости от первоначальных условий или промежуточных результатов необходимо выполнить вычисления по одним или другим формулам. Такие задачи можно описать с помощью алгоритмов разветвляющейся структуры. В таких алгоритмах выбор направления продолжения вычисления осуществляется по итогам проверки заданного условия. Ветвящиеся процессы описываются оператором IF (условие).
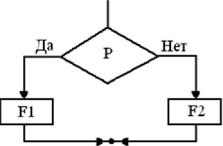
Разветвляющаяся структура (ветвление)– это структура, обеспечивающая альтернативный выбор в зависимости от заданного условия. Выполняется проверка условия, а затем выбирается один из путей. Если P – это условие, то в зависимости от его выполнения или невыполнения (истинности (Да) или ложности (Нет)), управление передается по одной из двух ветвей.
Может оказаться, что для одного из результатов проверки условия ничего предпринимать не надо. В этом случае можно применять только один обрабатывающий блок.
 |
 |
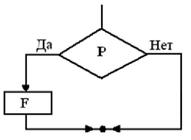Рис. 5. - Элементы блок-схемы ветвления
Эта структура называется также ЕСЛИ – ТО – ИНАЧЕ. Каждый из путей (ТО или ИНАЧЕ) ведет к общей точке слияния, так что выполнение программы продолжается независимо от того, какой путь был выбран.
Рассмотрим несколько примеров построения алгоритмов разветвленной структуры.
Пример 1.Известны коэффициенты а, b и с квадратного уравнения ax2+bx+c=0. Вычислить корни квадратного уравнения.
Решение. Входные данные: a, b, c. Выходные данные: х1, х2.Согласно формуле нахождения корней квадратного уравнения,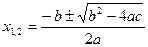 
. Величина 
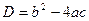, называемая дискриминантом, определяет, имеет ли уравнение два различных действительных корня 
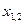(D>0), два одинаковых корня 
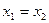(D=0), или не имеет действительных корней (D<0). Поэтому сначала по входным данным (значениям коэффициентов а, b и с)вычисляют дискриминантD,а затем, в зависимости от полученного значения, принимают решение относительно корней исходного уравнения.
|
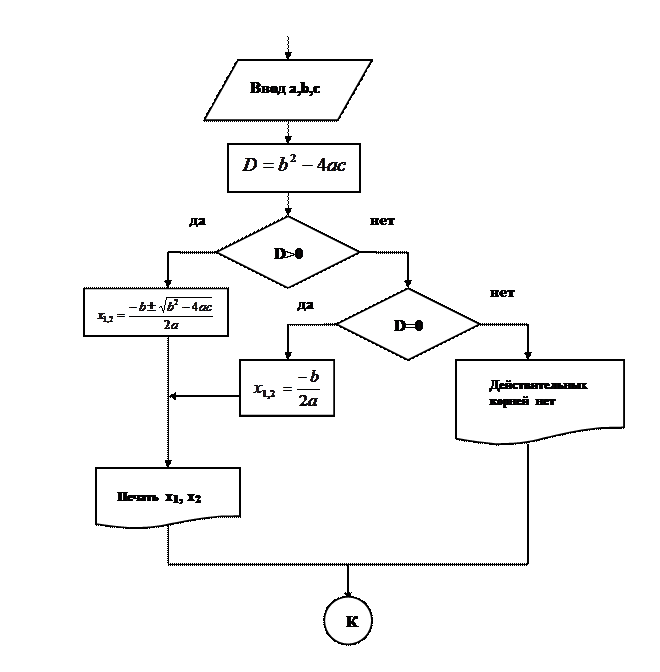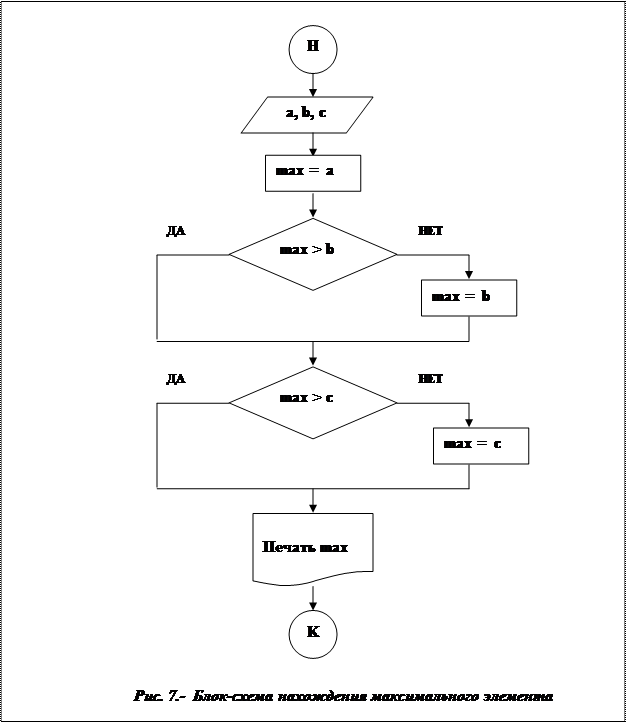
Рис. 6. - Блок-схема решения квадратного уравнения Пример 2.Составить блок-схему определениямаксимального из трех чисел a, b, c.
Решение. Входные данные: a, b, c. Выходные данные: max(а, b, c).Сначала предположим, что максимальным является первое число, т.е. a.Затемсравниваем текущее значение максимума со вторым числом b и выбираем большее из двух чисел (max, b).Полученный результат сравниваем с третьим числом и выбираем большее из последней пары.
Замечание. Элементы этого алгоритма используем в дальнейшем при решении задачи выбора максимального элемента массива данных.
