Лекция № 7. Методы обработки данных при анализе рынка

Лекция № 7. Методы обработки данных при анализе рынка

недвижимости. (4 часа)

Риэлтор должен ориентироваться в ценовой политике на рынке недвижимости, уметь прогнозировать цены, поведение участников рынка, и пр. Поэтому, необходимо разобраться с некоторыми определениями и методами обработки данных при анализе рынка недвижимости.

1. Основные определения

1) Случайная величина - это такая величина, которая может принимать различные значения под воздействием случайных (неконтролируемых факторов). Случайная величина может изменяться также и под воздействием неслучайных факторов, однако если закономерность их изменения неизвестна или конкретная задача не требует ее учета, то такие факторы относятся к случайным.

2) Генеральная совокупность значений случайной величины - это совокупность всех значений, которые она может принять под воздействием случайных факторов (стоимость всех квартир жилого фонда). Генеральная совокупность может разделяться на группы по неслучайному признаку.

3) Структура генеральной совокупности - это доля (процентный состав) в ней подсовокупностей, выделенных по одному или нескольким признакам.

4) Выборка - несколько значений случайной величины, выбранных из генеральной совокупности по случайному признаку.

5) Репрезентативность выборки - это ее достаточно близкое соответствие генеральной совокупности по основным характеристикам (прежде всего по структуре).

Способы описания случайной величины

1) Гистограмма - представление случайной величины в виде столбчатого графика, отражающего долю (количество) попаданий случайной величины в различные диапазоны ее значений.

2) Определение параметров случайной величины, характеризующих ее среднее значение и разброс случайной величины вокруг среднего. В качестве среднего значения случайной величины используются следующие величины:

а) Медианное значение случайной величины - это одно из ее значений в выборке, относительно которого половина значений превышает медианное значение, а другая половина не превышает.

б) Модальное значение случайной величины (мода) - это такое значение на гистограмме, которое соответствует середине диапазона с наибольшей высотой (наиболее вероятной значение).

в) Среднее арифметическое значение (математическое ожидание) случайной величины - это расчетная величина, определяемая по специальной формуле и соответствующая центру тяжести гистограммы.

Разброс случайной величины вокруг среднего значения характеризуется следующими параметрами:

а) Размах случайной величины - это разность между максимальным и минимальным ее значением.

б) Дисперсия (среднеквадратичное отклонение) - расчетная величина, отражающая отклонение каждого из значений случайной величины от среднего значения.

Среднее линейное отклонение отражает среднее абсолютное отклонение значений от их средней величины. При расчете этого показателя, чтобы избежать взаимопогашения положительных и отрицательных отклонений, используется модуль, то есть каждое отклонение от средней берется с положительным знаком. Та же идея лежит в расчете дисперсии, только отклонения берутся не по модулю, а возводятся в квадрат. Квадрат любого числа, как известно, всегда будет положительным.

Дисперсия в статистике очень важный показатель, который активно используется в других видах статистического анализа (проверка гипотез, анализ причинно-следственных связей и др.).

Как и среднее линейное отклонение, дисперсия также отражает меру разброса данных вокруг средней величины.

Как и математическое ожидание, дисперсия является важной характеристикой случайной величины. Если математическое ожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

в) Доверительный интервал - это размах случайной величины, определенный не по всем ее значениям, а по заданной доле значений (доверительной вероятности) примыкающих к среднему.

Правило двух сигм

Почти достоверно (с доверительной вероятностью 0,954) можно утверждать, что все значения случайной величины X с нормальным законом распределения отклоняются от ее математического ожидания M(X) = a на величину, не большую 2s (двух средних квадратических отклонений). Доверительной вероятностью (Pд) называют вероятность событий, которые условно принимаются за достоверные (их вероятность близка к 1).

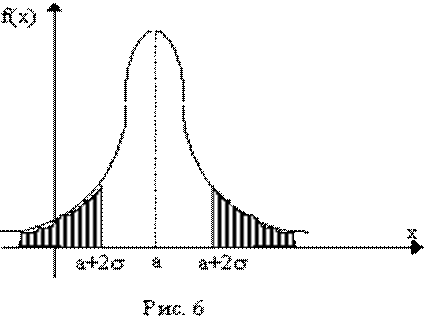
Проиллюстрируем правило двух сигм геометрически. На рис. 6 изображена кривая Гаусса с центром распределения а. Площадь, ограниченная всей кривой и осью Оx, равна 1 (100%), а площадь криволинейной трапеции между абсциссами а–2s и а+2s, согласно правилу двух сигм, равна 0,954 (95,4% от всей площади). Площадь заштрихованных участков равна 1-0,954 = 0,046 (»5% от всей площади). Эти участки называют критической областью значений случайной величины. Значения случайной величины, попадающие в критическую область, маловероятны и на практике условно принимаются за невозможные.

Вероятность условно невозможных значений называют уровнем значимости случайной величины. Уровень значимости связан с доверительной вероятностью формулой:

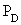= 1- ,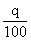

где q – уровень значимости, выраженный в процентах.

Правило трех сигм

При решении вопросов, требующих большей надежности, когда доверительную вероятность (Pд) принимают равной 0,997 (точнее - 0,9973), вместо правила двух сигм, согласно формуле (3), используют правило трех сигм.

Согласно правилу трех сигм при доверительной вероятности 0,9973 критической областью будет область значений признака вне интервала (а-3s, а+3s). Уровень значимости составляет 0,27%.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными. Т.е. выборка высокоточная.

В этом и состоит сущность правила трех сигм:

Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения (СКО).

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

Уровень значимости принимают в зависимости от дозволенной степени риска и поставленной задачи. Для оценки недвижимости обычно принимается менее точная выборка, следуя правилу двух сигм.

Лекция № 7. Методы обработки данных при анализе рынка

недвижимости. (4 часа)

Риэлтор должен ориентироваться в ценовой политике на рынке недвижимости, уметь прогнозировать цены, поведение участников рынка, и пр. Поэтому, необходимо разобраться с некоторыми определениями и методами обработки данных при анализе рынка недвижимости.

1. Основные определения

1) Случайная величина - это такая величина, которая может принимать различные значения под воздействием случайных (неконтролируемых факторов). Случайная величина может изменяться также и под воздействием неслучайных факторов, однако если закономерность их изменения неизвестна или конкретная задача не требует ее учета, то такие факторы относятся к случайным.

2) Генеральная совокупность значений случайной величины - это совокупность всех значений, которые она может принять под воздействием случайных факторов (стоимость всех квартир жилого фонда). Генеральная совокупность может разделяться на группы по неслучайному признаку.

3) Структура генеральной совокупности - это доля (процентный состав) в ней подсовокупностей, выделенных по одному или нескольким признакам.

4) Выборка - несколько значений случайной величины, выбранных из генеральной совокупности по случайному признаку.

5) Репрезентативность выборки - это ее достаточно близкое соответствие генеральной совокупности по основным характеристикам (прежде всего по структуре).