Лекция 10 Системы линейных уравнений

Показатели функционирования систем и процессов, экономические показатели часто оказываются взаимозависимыми. Структура связей между такими показателями (переменными) может быть описана с помощью системы (структурных) уравнений [3]. В этих уравнениях присутствуют переменных следующих типов:

- эндогенные, зависимые переменные y, определяемые внутри системы;

- экзогенные, независимые переменные x, значения которых задаются извне, они являются управляемыми, планируемыми;

- предопределенные переменные, включающие в себя как экзогенные переменные за текущий период времени, так и лаговые переменные (т.е. экзогенные и эндогенные переменные за предыдущие периоды времени).

Выделяют следующие виды систем.

1) Системы независимых уравнений, в которых каждая зависимая переменная y_i (i=1,…,n) представлена как функция одного и того же набора независимых переменных x_j (j=1,…,m):

y₁ = a₁₁ x₁+ a₁₂ x₂ + …+a_1m x_m + e₁

y₂ = a₂₁ x₁+ a₂₂ x₂ + …+a_2m x_m + e₂(1)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

y_n = a_n1 x₁+ a_n2 x₂ + …+a_nm x_m + e_n

Каждое уравнение этой системы можно рассматривать самостоятельно как уравнение регрессии. В него может быть введен свободный член, коэффициенты регрессии могут быть найдены методом наименьших квадратов (м.н.к).

2) Системы рекурсивных уравнений, в которых зависимые переменные y_i (i=1,…,n) представлены как функции независимых переменных x_j (j=1,…,m) и определенных ранее зависимых переменных y₁ , y₂ ,…, y_i-1:

y₁ = a₁₁ x₁ + a₁₂ x₂ + …+a_1m x_m + e₁

y₂ = b₂₁ y₁+ a₂₁ x₁ + a₂₂ x₂ + …+a_2m x_m + e₂(2)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

y_n = b_n1 y₁+ b_n2 y₂+,…,+b_nn-1 y_n-1 +a_n1 x₁+ a_n2 x₂ + …+a_nm x_m + e_n

Параметры каждого уравнения системы определяются отдельно, в последовательном порядке, начиная с первого уравнения, методом наименьших квадратов.

3) Системы взаимозависимых уравнений, в которых каждая зависимая переменная y_i (i=2,…,n) представлена как функция остальных зависимых переменных y_k (k ¹ i) и независимых (предопределенных) переменных x_j (j=1,…,m):

y₁= b₁₂ y₂+ b₁₃ y₃ + … + b_1n y_n +a₁₁ x₁+ a₁₂ x₂ + …+a_1m x_m + e₁

y₂= b₂₁ y₁+ b₂₃ y₃ + … + b_2n y_n +a₂₁ x₁+ a₂₂ x₂ + …+a_2m x_m + e₂(3)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

y_n= b_n1 y₁+ b_n2 y₂+ … + b_nn-1 y_n-1+a_n1 x₁ + a_n2 x₂ + …+a_nm x_m + e_n

Эта система наиболее распространенная, она получила также название системы совместных, одновременных уравнений. Ее так же называют структурной формой модели (СФМ).

Отдельные коэффициенты при переменных СФМ могут быть равны нулю, что означает отсутствие в уравнении этих переменных. Например, модель динамики цены и заработной платы может быть описана СФМ следующего вида:

y₁= b₁₂ y₂+a₁₁ x₁+ e₁

y₂= b₂₁ y₁+ a₂₂ x₂ +a₂₃ x₃ + e₂(4)

где y₁– темп изменения заработной платы;

y₂– темп изменения цен;

x₁– процент безработных;

x₂– темп изменения постоянного капитала;

x₃– темп изменения цен на импорт сырья.

Данная система из двух уравнений содержит две зависимые, эндогенные (y₁, y₂) и три независимые, экзогенные (x₁, x₂, x₃) переменные. В первом уравнении отсутствуют переменные x₂ и x₃ . Это значит, что коэффициенты a₁₂= 0и a₁₃= 0.

В СФМ для нахождения параметров модели b_ij и a_ij (называемых также структурными коэффициентами модели), простой м.н.к. неприменим.

Обычно для определения структурных коэффициентов модели СФМ преобразуется в приведенную форму модели (ПФМ):

y₁ = d₁₁ x₁ + d₁₂ x₂ + …+d_1m x_m

y₂ = d₂₁ x₁+ d₂₂ x₂ + …+d_2m x_m (5)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

y_n = d_n1 x₁+ d_n2 x₂ + …+d_nm x_m

Параметры приведенной формой модели dij могут быть оценены по методу наименьших квадратов. По этим параметрам затем рассчитываются структурные коэффициенты модели b_ij и a_ij. Для существования однозначного соответствия между параметрами структурной и приведенной формами необходимо выполнение условия идентификации.

Структурные формы модели могут быть:

- идентифицируемые;

- неидентифицируемые;

- сверхидентифицируемые.

Для того, чтобы СФМ была идентифицируема, необходимо чтобы каждое уравнение системы было идентифицируемо. В этом случае число параметров СФМ равно числу параметров приведенной формы.

Если хотя бы одно уравнение СФМ неидентифицируемо, то вся модель считается неидентифицируемой. В этом случае число коэффициентов приведенной формы модели меньше, чем число коэффициентов СФМ.

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае можно получить два и более значений одного структурного коэффициента на основе коэффициентов приведенной формы модели. В сверхидентифицируемой модели хотя бы одно уравнение сверхидентифицируемо, а остальные уравнения идентифицируемы.

Если обозначить число эндогенных переменных в i-том уравнении СФМ через Н, а число предопределенных переменных, которые содержатся в системе, но не входят в данное уравнение, через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

если D+1 < H уравнение неидентифицируемо;

если D+1 = H уравнение идентифицируемо;

если D+1 > H уравнение сверхидентифицируемо;

Счетное правило является необходимым, но не достаточным условием идентификации. Кроме этого правила для идентифицируемости уравнения должно выполняться дополнительное условие.

Отметим в системе эндогенные и экзогенные переменные, отсутствующие в рассматриваемом уравнении, но присутствующие в системе. Из коэффициентов при этих переменных в других уравнениях составим матрицу. При этом если переменная стоит в левой части уравнения, то коэффициент надо брать с обратным знаком.

Если определитель полученной матрицы не равен нулю, а ранг не меньше, чем количество эндогенных переменных в системе без одного, то достаточное условие индетификации для данного уравнения выполнено.

Поясним это на примере следующей структурной модели.

y₁= b₁₂ y₂+ b₁₃ y₃ + a₁₁ x₁+ a₁₂ x₂

y₂= b₂₁ y₁ + a₂₂ x₂+ a₂₃ x₃ + a₂₄ x₄ (6)

y₃= b₃₁ y₁+ b₃₂ y₂+a₃₁ x₁+ a₃₂ x₂

Проверим каждое уравнение системы на выполнение неоходимого и достаточного условия идентификации.

В первом уравнении три эндогенных переменных: y₁, y₂и y₃ (H=3). В нем отсутствуют экзогенные переменные x₃и x₄ (D=2). Необходимое условие идентификации D+1=H выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных x₃и x₄ (см. таблицу 1). В первом столбце таблицы показано, что коэффициенты при экзогенных переменных x₃и x₄взяты из уравнений 2 и 3 системы. Во втором уравнении эти переменные присутствуют и коэффициенты при них равны a₂₃и a₂₄ соответственно. В третьем уравнении эти переменные отсутствуют, т.е. коэффициенты при них равны нулю. Так как вторая строка матрицы состоит из нулей, определитель матрицы равен нулю. Значит, достаточное условие не выполнено, и первое уравнение нельзя считать идентифицируемым.

Во втором уравнении две эндогенные переменные: y₁ и y₂(H=2). В нем отсутствует экзогенная переменная x₁(D=1). Необходимое условие идентификации D+1=H выполнено

Таблица 1 - Матрица, составленная из коэффициентов при x₃и x₄.

Уравнения, из которых взяты коэффициенты при переменных	Переменные
x3	x4
	a23	a24

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных y₃и x₁ , которые отсутствуют во втором уравнении (см. таблицу 2).

Таблица 2 - Матрица, составленная из коэффициентов при переменных y₃и x₁.

Уравнения, из которых взяты коэффициенты при переменных	Переменные
y3	x1
	b13	a11
	-1	a31

В третьем уравнении при переменной y₃коэффициент равен –1, так как эта переменная стоит в левой части уравнения. Действительно, третье уравнение можно записать в виде 0= b₃₁ y₁ + b₃₂ y₂-1 y₃ +a₃₁ x₁+ a₃₂ x₂ и тогда равенство b₃₃ = –1 становится очевидным.

В общем случае СФМ может быть представлена в виде матрицы коэффициентов при переменных. В этом случае третье уравнение может быть задано вектором (b₃₁ , b₃₂ , -1, a₃₁, a₃₂, 0 , 0) , а вся система одновременных уравнений (6) будет представлена матрицей (7):

(7)

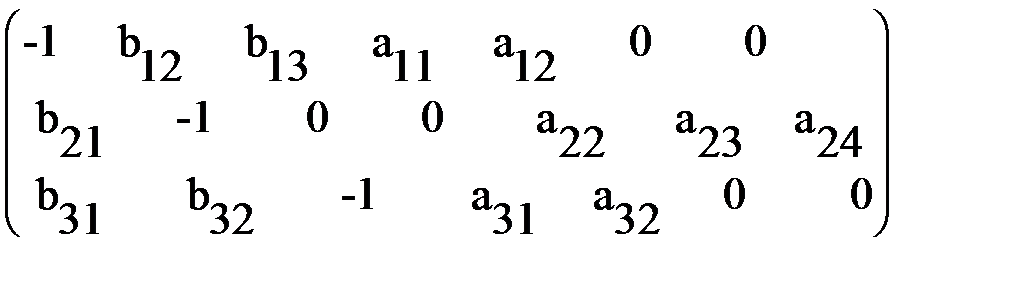
В примерах и задачах СФМ представляют в виде такой матрицы коэффициентов при переменных модели.

Определитель представленной в таблице 2 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и второе уравнение идентифицируемо.

В третьем уравнении три эндогенные переменные: y₁, y₂ и y₃ (H=3). В нем отсутствует экзогенные переменные x₃и x₄ (D=2). Необходимое условие идентификации D+1=H выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных х₃и x₄ , которые отсутствуют в третьем уравнении (см. таблицу 3). Согласно таблице, определитель матрицы равен нулю (первая строка состоит из нулей). Значит, достаточное условие не выполнено, и третье уравнение нельзя считать идентифицируемым.

Таблица 3 - Матрица, составленная из коэффициентов при переменных x₃и x₄.

Уравнения, из которых взяты коэффициенты при переменных	Переменные
x3	x4
	0	0
	a23	a24

В эконометрических моделях иногда используются балансовые тождества переменных (например, вида y₃= y₁+ y₂+ x₁). Коэффициенты при переменных при этом не требуют оценок и уравнение не надо исследовать на идентификацию, но в проверке на идентификацию всей системы эти уравнения участвуют. Присутствующие иногда в моделях свободные и остаточные члены (а₀₁, а₀₂ , а₀₃ ,…e₁, e₂, e₃,…) не влияют на решение вопроса об идентификации.

При оценивании коэффициентов структурной модели используется ряд методов. С этими методами можно ознакомиться в рекомендованной литературе [3].

Рассмотрим косвенный метод наименьших квадратов (к.м.н.к.), который применяется в случае точно идентифицируемой структурной модели. Рассмотрим этот метод на примере следующей идентифицируемой модели, содержащей две эндогенные и две экзогенные переменные:

y₁= b₁₂ y₂ + a₁₁ x₁ + e₁ (8)

y₂= b₂₁ y₁ + a₂₂ x₂ + e₂

Для построения модели мы располагаем информацией, представленной в таблице 4.

Таблица 4 - Фактические данные для построения модели

n	у1	у2	х1	х2
	33,0	37,1
	45,9	49,3
	42,2	41,6
	51,4	45,9
	49,0	37,4
	49,3	52,3
Сумма	270,8	263,6
Средн. знач.	45,133	43,930	7,500	10,333

Структурную модель преобразуем в приведенную форму модели:

y₁= d₁₁ x₁ + d₁₂ x₂ + u_{1 ,} (9)

y₂= d₂₁ x₁ + d₂₂ x₂ + u_{2 ,}

где u₁ и u₂ – случайные ошибки.

Для каждого уравнения приведенной формы при расчете коэффициентов d можно применить м.н.к..

Для упрощения расчетов можно работать с отклонениями от средних уровней y=y-y_cp и x=x-x_cp (y_cp и x_cp – средние значения). Преобразованные таким образом данные таблицы 4 сведены в таблицу 5. Здесь же показаны промежуточные расчеты, необходимые для определения коэффициентов d_ik. Переменные, означающие отклонение от средних значений изображаются далее жирным шрифтом и курсивом.

Для нахождения коэффициентов d_1k первого приведенного уравнения можно использовать следующую систему нормальных уравнений:

Σ y₁ x₁= d₁₁ Σ x₁²+ d₁₂ Σ x₁ x₂ (10)

Σ y₁ x₂= d₁₁ Σ x₁ x₂ + d₁₂ Σ x₂²

Таблица 5 - Преобразованные данные для построения приведенной формы модели

n	у1	у2	х1	х2	у1*х1	х12	х1*х2	у1*х2	у2*х1	у2*х2	х22
	-12,133	-6,784	-4,500	0,667	54,599	20,250	-3,002	-8,093	30,528	-4,525	0,445
	0,767	5,329	-0,500	5,667	-0,383	0,250	-2,834	4,347	-2,664	30,198	32,115
	-2,933	-2,308	-0,500	-1,333	1,467	0,250	0,667	3,910	1,154	3,077	1,777
	6,267	1,969	2,500	-1,333	15,668	6,250	-3,333	-8,354	4,922	-2,625	1,777
	3,867	-6,541	2,500	-9,333	9,667	6,250	-23,333	-36,091	-16,353	61,048	87,105
	4,167	8,337	0,500	5,667	2,084	0,250	2,834	23,614	4,168	47,244	32,115
Сумма	0,002	0,001	0,000	0,002	83,102	33,500	-29,001	-20,667	21,755	134,417	155,334

Подставляя рассчитанные в таблице 5 значения сумм в (10), получим:

83,102= 33,5 d₁₁ - 29,001d₁₂ (11)

-20,667= -29,001d₁₁ + 155,334d₁₂

Решение этих уравнений дает значения d₁₁ = 2,822 и d₁₂ = 0,394. Первое уравнение приведенной формы модели примет вид:

y₁= 2,822 x₁ + 0,394 x₂ + u₁ (12)

Для нахождения коэффициентов d_2k второго приведенного уравнения можно использовать следующую систему нормальных уравнений:

Σ y₂ x₁= d₂₁ Σ x₁² + d₂₂ Σ x₁ x₂(13)

Σ y₂ x₂= d₂₁ Σ x₁ x₂ + d₂₂ Σ x₂²

Подставляя рассчитанные в таблице 5 значения сумм в (13), получим

21,755 = 33,5 d₂₁ - 29,001d₂₂

134,417= -29,001d₂₁ + 155,334d₂₂ . (14)

Решение этих уравнений дает значения d₂₁ =1,668 и d₂₂ =1,177. Второе уравнение приведенной формы модели примет вид:

y₂= 1,668 x₁ + 1,177 x₂ + u_2. (15)

Для перехода от приведенной формы к структурной форме модели найдем x₂ из второго уравнения (15) приведенной формы модели:

x₂= (y₂ - 1,668 x₁ ) / 1,177.

Подставим это выражение в первое уравнение (12) приведенной модели найдем структурное уравнение

y₁= 2,822 x₁ + 0,394 (y₂ - 1,668 x₁ ) / 1,177 =

= 2,822 x₁ + 0,335 y₂ - 0,558 x₁ = 0,335 y₂ + 2,264 x₁

Таким образом, b₁₂ = 0,335; a₁₁ = 2,264.

Найдем x₁ из первого уравнения (12) приведенной формы модели:

x₁ = (y₁ - 0,394 x₂ ) / 2,822.

Подставим это выражение во второе уравнение (15), приведенной модели, найдем структурное уравнение:

y₂= 1,177 x₂ + 1,668 (y₁ - 0,394 x₂ ) / 2,822 =

= 1,177 x₂ + 0,591 y₁ - 0,233 x₂ = 0,591 y₁ + 0,944 x₂

Таким образом, b₂₁ = 0,591; a₂₂ = 0,944.

Свободные члены структурной формы находим из уравнений:

а₀₁= y_1,cp - b₁₂ y_2,cp - a₁₁ x_1,cp =

=45,133 – 0,335 * 43,93 –2,264* 7,5 = 13,436;

а₀₂= y_2,cp - b₂₁ y_1,cp - a₂₂ x_2,cp =

=43,93 – 0,591* 45,133 - 0,944 * 10,333= 7,502.

Окончательный вид структурной модели:

y₁= a₀₁+ b₁₂ y₂ + a₁₁ x₁ + e₁= 13,436 + 0,335 y₂ + 2,264 x₁ + e_1; (16)

y₂= a₀₂+ b₂₁ y₁ + a₂₂ x₂ + e₂= 7,502 + 0,591 y₁ + 0,944 x₂ + e_2.

Контрольные вопросы

1. Что представляет собой система линейных уравнений?

2. Особенности системы независимых уравнений. Методы решения.

3. Особенности системы рекурсивных уравнений. Методы решения.

4. Особенности системы взаимозависимых уравнений. Методы решения.

5. Структурные формы модели системы взаимозависимых уравнений.

6. Косвенный метод наименьших квадратов.