Методы шифрования на основе датчика псевдослучайных чисел

Принцип шифрования заключается в генерировании псевдослучайной последовательности, называемой гаммой, и наложении гаммы на открытое сообщение некоторым обратимым образом.

Например, если открытые данные и гамма представлены в двоичном коде, то подходящей является операция сложения по модулю 2; если исходным является русский текст, то в качестве гаммы можно использовать последовательность независимых псевдослучайных целых чисел от 1 до 33 с равными вероятностями, а операция наложения будет заключаться в сложении номеров букв с числами гаммы по модулю 33 и т.д. Расшифрование требует повторного генерирования гаммы и применения обратной операции (в рассмотренных случаях вычитания по соответствующему модулю). Ключом в данном случае может служить некоторый параметр датчика псевдослучайных чисел.

Линейный датчик псевдослучайных чисел реализуется на цифровой вычислительной машине и описывается рекуррентной формулой

g_i+1 = [Ag_i + C]mod M,

где g_i, i = 1, 2, 3, … – последовательность псевдослучайных чисел,

g₀ – стартовое значение,

A и C – некоторые константы. Обычно принимается M = 2^b, где b – разрядность машины.

Если гамма имеет период больший, чем длина зашифрованного сообщения, и если не известна никакая часть исходного текста, то этот шифр можно раскрыть только прямым перебором возможных ключей, поэтому криптостойкость определяется размером ключа [18].

Шифрование на основе датчиков псевдослучайных чисел наиболее часто применяется в программной реализации криптозащиты данных, так как, с одной стороны, он достаточно прост для про граммирования, а с другой стороны, обладает высокой криптостойкостью.

Одной из форм реализации описанного метода является метод «одноразового блокнота». Суть этого метода состоит в том, что у шифровальщиков на передающей и приемной сторонах имеются два идентичных блокнота с одинаковой гаммой, содержащей случайные независимые равновероятные числа. Эта гамма, являющаяся ключом, используется только один раз, после чего соответствующий лист блокнота вырывается и уничтожается. Если эти условия соблюдены, шифр является абсолютно криптостойким, т.е. не может быть взломан в принципе [20]. Однако этот метод очень сложно реализовать, так как трудно снабдить всех возможных получателей шифртекстов идентичными шифровальными блокнотами и обеспечить их однократное использование. Абсолютно стойкие шифры применяются только в системах секретной связи с небольшим объемом передаваемой информации, обычно для передачи особо важной государственной информации [21].

Методы перемешивания

Методы перемешивания основаны на работе К. Шеннона [19], в которой задачи криптологии рассматривались с информационной точки зрения. Прежде чем перейти к конкретным системам шифрования на основе перемешивания, приведем основные положения работы Шеннона.

Основные вопросы, которые представляют интерес с теоретической точки зрения, состоят в следующем. Насколько устойчива система, если шифровальщик противника располагает всеми необходимыми средствами для криптоанализа и неограниченным временем? Имеет ли криптограмма единственное решение (даже если оно может быть найдено за практически неприемлемое время), а если нет, то сколько решений она имеет? Какой объем шифрованного текста нужно перехватить, чтобы решение стало единственным? Существуют ли секретные системы, для которых нельзя найти единственное решение независимо от объема перехваченной криптограммы? Существуют ли системы, в которых противник вообще не получает никакой информации независимо от объема перехваченного шифртекста? Рассмотрение этих вопросов основывается на понятиях теории информации.

Пусть имеется конечное множество сообщений M₁,… M_n с априорными вероятностями P(M₁) , P(M₂) ,…, P(M_n) и эти со общения преобразуются в криптограммы E₁, E₂, …, E_n, так что E = T_i{M}.

После перехвата криптограммы E шифровальщик противника может вычислить условные (апостериорные) вероятности различных сообщений P_E(M) = P(M | E). Тогда совершенная секретная система удовлетворяет следующему условию: для всех E все апостериорные вероятности равны априорным

.

В этом и только в этом случае перехват шифртекста не дает противнику никакой информации.

По теореме Байеса

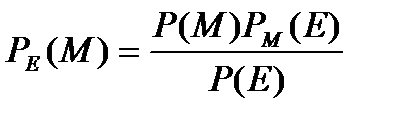, (23.1)

где P(M) – априорная вероятность сообщения M;

P_M(E) – условная вероятность криптограммы E при условии, что выбрано сообщение M;

P(E) – вероятность получения криптограммы E;

P_E(M) – апостериорная вероятность сообщения M при условии, что перехвачена криптограмма E.

Из выражения (23.1) следует, что для совершенной секретности необходимо и достаточно, чтобы выполнялось равенство P_M(E) = P(E) для любых сообщения M и криптограммы E.

Очевидно, различных криптограмм должно быть не меньше, чем различных сообщений, так как при любом ключе сообщению M должна однозначно соответствовать криптограмма E, которой, в свою очередь, однозначно соответствует сообщение M. Кроме того, число различных ключей должно быть также не меньше, чем различных сообщений. Например, совершенная система получается, если число сообщений равно числу ключей и числу криптограмм, причем все ключи равновероятны [19].

В терминах теории информации секретная система содержит два источника неопределенности: источник сообщений с энтропией

,

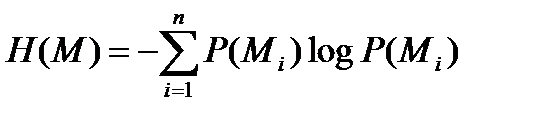и источник ключей с энтропией

.

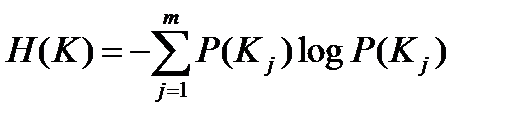Количество информации источника не может быть больше, чем log n (это количество соответствует равновероятным сообщениям). Эта информация может быть полностью скрыта, только если неопределенность ключа не меньше log n. Таким образом, неопределенность источника ключей устанавливает предел – максимальное количество информации, которое может быть скрыто при помощи ключей данного источника.

Если источник порождает последовательности бесконечной длины, то никакой конечный ключ не дает совершенной секретности. Пусть длина сообщения равна N, а длина ключа M. Тогда для совершенной секретности требуется

N log n ≤ M log m,

где n и m – объемы алфавитов для сообщений и ключей соответственно.

Совершенные системы применяются на практике для засекречивания сравнительно коротких сообщений и в тех случаях, когда полной секретности придается чрезвычайное значение.

В качестве теоретической меры секретности Шеннон предложил использовать ненадежность. Имеются две ненадежности:

ненадежность ключа

, (23.2)

и ненадежность сообщения

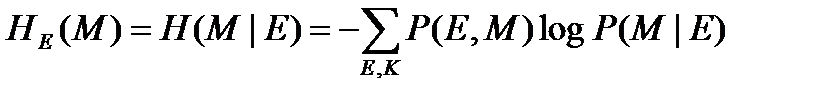, (23.3)

где P(E, M) – совместная вероятность криптограммы E и сообщения M, P(E, K) – совместная вероятность криптограммы E и ключа K, P(M | E) и P(K | E) – апостериорные вероятности для сообщения и ключа при условии перехвата криптограммы E. Суммирование в (23.2) и (23.3) проводится по всем возможным криптограммам и ключам (соответственно по всем возможным криптограммам и сообщениям) определенной длины, поэтому ненадежности зависят от числа N перехваченных букв криптограммы. Постепенное убывание ненадежностей с ростом N соответствует увеличению сведений о ключе и сообщении, имеющихся у шифровальщика противника. Если ненадежность становится нулевой, это означает, что единственное сообщение (или единственный ключ) имеет апостериорную вероятность 1, а все остальные – нулевые апостериорные вероятности. Шеннон доказал, что в принципе можно построить систему, в которой ненадежности не стремятся к нулю при 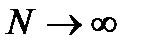, и даже «строго идеальную систему», в которой H_E(K) = H(K). Для сообщений на естественных языках характерны неравновероятность и зависимость букв исходного текста, поэтому для них построение идеальной системы хотя и возможно, но осуществить его практически очень сложно [19].

Статистическая зависимость символов (букв) естественного языка позволяет раскрывать многие типы шифров. Например, шифры на основе подстановок раскрываются на основе простого подсчета частот встречаемости различных букв в криптограмме и сравнения их с известными для данного языка частотами. Для некоторых шифров могут потребоваться более тонкие методы статистического анализа. В любом случае статистический анализ криптограмм строится на основе некоторых статистик. Под статистикой понимается функция наблюдаемой криптограммы, значение которой позволяет сделать какие-либо более или менее правдоподобные выводы относительно использованного ключа. Удачный выбор подходящих статистик определяет успех криптоаналитика при взломе шифра, многократно сужая возможный круг ключей до того предела, когда уже можно установить правильный ключ путем перебора.

Для того чтобы затруднить раскрытие шифров статистическими методами, Шеннон предложил использовать две идеи, которые он назвал «распылением» и «запутыванием». Смысл «распыления» состоит в таком преобразовании текста, при котором статистические связи между его элементами становятся трудно наблюдаемыми, хотя избыточность сообщения при этом и не изменяется. Идея «запутывания» (перемешивания) заключается в том, чтобы сделать соотношения между простыми статистиками в пространстве криптограмм и простыми подмножествами в пространстве ключей весьма сложными и беспорядочными [19]. На этих идеях основано использование составных шифров, состоящих часто в последовательном применении простых подстановок и перестановок.

В шифрах подстановки буквы сообщения заменяются другими буквами, поэтому статистические свойства текста сохраняются, но относятся теперь к буквам другого алфавита. В шифрах перестановки буквы сообщения остаются теми же, но изменяется их расположение в тексте. Комбинирование поочередно применяемых подстановок и перестановок дает возможность создавать весьма стойкие шифры.

Один из примеров реализации такого подхода – государственный стандарт шифрования США, известный под названием DES (Data Encryption Standard). Алгоритм шифрования является открытым; секретным при каждом использовании алгоритма является только ключ. Ключ длиной в 56 бит обеспечивает высокий уровень стойкости шифра, так как общее количество ключей составляет около 7,2·10¹⁶. Открытый текст и криптограмма при этом являются двоичными 64-значными последовательностями. Криптоалгоритм DES представляет собой суперпозицию из 16 последовательных шифроциклов, в каждом из которых происходят подстановки и перестановки в четырехбитовых группах, при этом в каждом цикле используются 48 бит ключа, которые выбираются из полного ключа длиной в 56 бит [18]. По утверждению Национального бюро стандартов США, метод DES имеет высокую криптостойкость, которая делает его раскрытие дороже получаемой при этом прибыли, экономичен в реализации и эффективен в смысле быстродействия.

Наиболее существенным недостатком считается слишком короткий ключ: для дешифрования требуется перебрать 2⁵⁶ (или 7,2·10¹⁶) ключей, что достаточно много для современной аппаратуры, но может оказаться преодолимым в ближайшем будущем. Впрочем, метод допускает простую модификацию в виде последовательного применения к сообщению нескольких циклов шифрования с различными ключами: например, уже при трех ключах для дешифрования требуется выполнение около 2¹⁶⁸ (т.е. 3,7·10⁵⁰) операций.

Отечественный стандарт шифрования данных, предусмотренный ГОСТ 28147-89, предназначен для шифрования данных аппаратным или программным путем [18]. Стандарт предусматривает различные режимы шифрования, но в любом случае используется 256-разрядный двоичный ключ. Двоичные данные, подлежащие зашифрованию, разбиваются на блоки по 64 разряда, над которыми выполняются преобразования, включающие суммирования по модулям 2, 2³² и 2³²–1, подстановки и циклические сдвиги. Стандарт обладает всеми достоинствами алгоритма DES и в то же время свободен от его недостатков, однако имеет собственный существенный недостаток – очень низкое быстродействие при программной реализации [18].