Пропускная способность каналов радиотехнической системы связи

Скорость передачи информации определяется средним количеством информации, которое получают на выходе канала связи в единицу времени. При вычислении скорости передачи информации в канале связи с помехами необходимо учитывать потери информации из-за действия помех.

Для дискретного канала связи скорость передачи информации находится по формуле

R_ДК = [H(U) - H_пот(U)]/ t_ср;

для непрерывного канала связи скорость передачи информации определится как

R_НК = 2F_m[h(U) - h_пот(U)],

где H(U) – энтропия передаваемого дискретного первичного сигнала; h(U) – дифференциальная энтропия передаваемого непрерывного сигнала; h_пот(U) – соответственно энтропии потерь в канале для дискретного и непрерывного первичных сигналов; t_ср – средняя длительность дискретного первичного сигнала; F_m – максимальная частота спектра непрерывного первичного сигнала.

Наибольшее значение скорости R передачи информации по каналу связи при заданных ограничениях называют пропускной способностью канала связи. Под заданными ограничениями понимают тип канала связи (дискретный или непрерывный), характеристики сигналов и помех.

Пропускная способность двоичного дискретного канала определяется так:

C_ДК =В[1 + p∙log p + (1 - р) log(1 - p)].

Для рассматриваемой радиотехнической системы морской связи определим пропускную способность при В = 50 Бод и вероятностях ошибок:

для АМ: P_АМ = 2∙10^-2,

С_АМ = 50[1 + 2∙10^-2 log 2∙10^-2 + 0,98 log 0,98] = 47,12 бит/с;

для ЧМ: P_ЧМ = 1,57∙10^-3,

С_АМ = 50[1 + 1,57∙10^-3 log 1,57∙10^-3 + 0,99843 log 0,99843] = 49,15 бит/с;

для ФМ: P_ФМ = 1,62∙10^-5,

С_АМ = 50[1 + 1,62∙10^-5 log 1,62∙10^-5 + 0,999 log 0,999] ≈ 50 бит/с.

Для непрерывного канала максимальная скорость передачи информации достигается для гауссовского канала с постоянными параметрами, при условии, что для сигнала распределение вероятностей мгновенных значений при ограниченной средней мощности близко к нормальному распределению.

Расчетная формула пропускной способности гауссовского канала, которая выведена Шенноном и носит его имя, имеет вид:

С_НК = F∙log(1+ P_c/P_п),

где F – ширина полосы пропускания канала; P_c/P_п – отношение сигнал/помеха по мощности.

Для рассматриваемой радиотехнической системы морской связи определим пропускную способность канала передачи информации с учетом ширины полосы пропускания для сигнала с частотной модуляцией F ≈ 2Δf = 6,2 кГц и отношения сигнал/помеха по мощности P_c/P_п = 1,47² =2,16. Тогда

С_НК = F∙log(l + P_c/P_п) = 6200∙log(l + 2,16)= 10290 бит/с.

Для рассматриваемой радиотехнической системы морской связи величина пропускной способности должна быть намного больше производительности источника сообщений и удовлетворять основной теореме Шеннона. Эта теорема формулируется так: если производительность источника меньше пропускной способности канала, то существует способ кодирования (преобразования сообщения в сигнал на входе) и декодирования (преобразования сигнала в сообщение на выходе канала), при котором вероятность ошибочного декодирования может быть сколь угодно мала.

ТЕОРЕТИКО-ИНФОРМАЦИОННАЯ КОНЦЕПЦИЯ КРИПТОЗАЩИТЫ СООБЩЕНИЙ В ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМАХ

ОСНОВЫ КРИПТОЗАЩИТЫ СООБЩЕНИЙ В СИСТЕМАХ СВЯЗИ

Основные понятия криптографии

Информация, которая нуждается в защите, называется защищаемой (приватной, конфиденциальной, секретной). Принято говорить, что такая информация содержит тайну (государственную, коммерческую, врачебную, личную, тайну следствия и т.п.).

Во всех случаях имеется круг законных пользователей информации. Кроме того, могут существовать люди или группы людей, которые заинтересованы в том, чтобы использовать информацию в своих целях, а значит – во вред законным пользователям. Для краткости эти незаконные пользователи называются противниками. Действия противника представляют угрозу для законного пользователя (угрозу разглашения, подмены, имитации, уничтожения информации и т.п.).

Возможны три подхода к защите информации [17]:

- создание абсолютно надежного канала связи, совершенно недоступного для незаконных пользователей;

- передача информации по общедоступному каналу, сохраняя в тайне сам факт передачи;

- передача информации по общедоступному каналу в такой форме, чтобы воспользоваться ею мог только адресат.

Первый способ при современном развитии техники практически нереализуем или сопряжен с чрезвычайно большими затратами.

Реализацией второго способа занимается стеганография. Известно немало примеров стеганографического сокрытия информации: от нанесения сообщения на обритую голову раба, которого посылали к адресату после того, как волосы отрастали, до использования симпатических чернил, которыми секретное сообщение вписывается между строк другого сообщения.

В настоящее время используется, например, прием, состоящий в выборочной записи символов сообщения в младшие разряды цифрового изображения – на качество его визуального восприятия эти искажения практически не влияют, а найти «спрятанные» данные в больших массивах, которыми представляются изображения, не так легко.

Третий способ – криптографическая защита информации путем шифрования – в настоящее время является одним из самых эффективных. Следует различать понятия кода и шифра.

Задачей криптографии является разработка методов преобразования сообщений, затрудняющих (в идеале – исключающих) извлечение противником информации из перехватываемых сообщений. По открытому каналу связи при этом передается криптограмма (шифртекст) – результат преобразования сообщения с помощью шифра (криптографического алгоритма). Наблюдение криптограммы для противника, не имеющего ключа, является бесполезным с точки зрения получения информации.

Зашифрованием называется процесс преобразования открытого сообщения в зашифрованное (криптограмму) с помощью шифра, а расшифрованием – обратный процесс преобразования зашифрованных (закрытых) данных в открытые с помощью шифра (шифрование – общее наименование для зашифрования и расшифрования).

Дешифрованием (вскрытием, взломом) называют процесс преобразования зашифрованных данных в открытые при неизвестном (частично или полностью) шифре. Решением всех перечисленных задач занимается наука, называемая криптологией. Отрасль криптологии, занимающаяся разработкой методов шифрования, называется криптографией, а отрасль, занимающаяся разработкой методов взлома – криптоанализом.

Помимо получения информации из перехваченного сообщения противник может преследовать и другие цели, например, он может попытаться изменить содержание сообщения. В защищенной системе, таким образом, получатель сообщения должен иметь возможность проверить его подлинность и целостность. Защита от навязывания ложных данных называется имитозащитой. Для этого к криптограмме добавляется имитовставка, представляющая собой последовательность данных фиксированной длины, полученную по определенному алгоритму из открытых данных и ключа. Получатель зашифрованного сообщения может проверить, соответствует ли имитовставка содержанию расшифрованного сообщения.

Криптостойкостью называется характеристика шифра, определяющая его способность противостоять дешифрованию. Обычно количественной мерой криптостойкости считается время, необходимое для дешифрования [18].

Проблема криптозащиты существует многие сотни лет, что естественно, если вспомнить, что у любого человека есть свои секреты. Математические основы криптографии были разработаны К. Шенноном [19]. В общем случае секретная система связи может быть представлена структурной схемой, показанной на рис. 23.1.

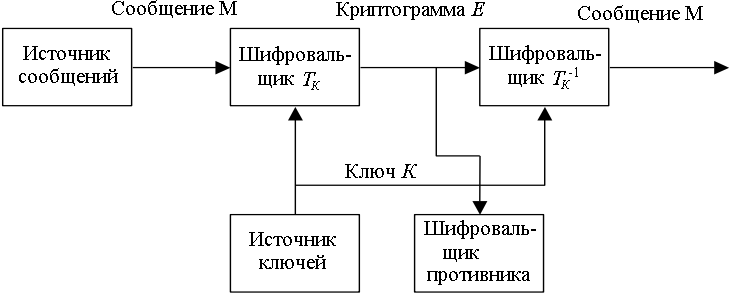
Рис. 23.1. Структура секретной системы

Сообщение M , вырабатываемое источником сообщений, поступает к шифровальщику. Шифровальщиком может быть как человек, так и устройство. От источника ключей к шифровальщику поступает ключ K. Шифровальщик на основе ключа осуществляет преобразование сообщения в криптограмму E = f(M, K).

Удобнее понимать это выражение не как функцию двух переменных, а как отображение E = T_K{M}, при этом ключ играет роль параметра этого отображения. Выбранный ключ должен быть каким-то образом передан (сообщен) шифровальщику на приемной стороне системы, который при помощи ключа расшифровывает сообщение. Чтобы секретная система была пригодной для передачи информации, необходимо иметь возможность восстановить по криптограмме и ключу исходное сообщение, т.е. должно существовать (единственное) обратное отображение, так что

M = T_K^-1{E} = T_K^-1{T_K[M]},

T_K^-1T_K = I,

где I – тождественное отображение.

Предполагается, что множество всех сообщений конечно и сообщения M₁,… M_n вырабатываются источником с вероятностями q₁,…, q_n. Аналогично источник ключей вырабатывает ключи K₁,…, K_m с вероятностями p₁,…, p_m.

В современной криптографии принято считать, что противнику известно множество отображений 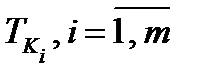и набор априорных вероятностей p₁,…, p_m.

Это предположение является пессимистическим, но, в конечном счете, реалистическим, так как рано или поздно всякая секретная система может быть раскрыта [19]. Если противник не сможет взломать алгоритм шифрования, даже зная, как он устроен, то тем более это окажется ему не по силам без такого знания.

В настоящее время используются следующие криптографические методы защиты [18]:

- методы замены (подстановки);

- методы на основе датчика псевдослучайных чисел;

- методы перемешивания (алгоритмические);

- системы с открытым ключом.

Метод замены

Для примера используем буквы русского алфавита (без буквы «ё») плюс пробел, обозначаемый символом ‗. Для удобства приведем русский алфавит в виде таблицы, содержащей также номера букв.

Буква	А	Б	В	Г	Д	Е	Ж	З	И	Й	К
№
Буква	Л	М	Н	О	П	Р	С	Т	У	Ф	Х
№
Буква	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я	_
№

В качестве примера рассмотрим шифр простой подстановки. В основе шифрования этим методом лежит алгебраическая операция над алфавитом сообщения, называемая подстановкой.

Подстановкой называется взаимно однозначное отображение конечного множества M на себя. Это означает, что каждому элементу множества (например, символу алфавита) ставится в соответствие один и только один элемент этого же множества. Очевидно, для задания конкретной подстановки природа элементов не имеет значения, важно лишь их количество N (называемое степенью подстановки). Можно поэтому в качестве множества рассматривать множество целых чисел М = {1, 2, 3, ..., N}.

Любая подстановка может быть описана матрицей 2 × N, в которой первая строка содержит числа 1, 2, …, N, а вторая строка состоит из тех же чисел, расположенных в порядке, определяемом подстановкой, например, если число i после подстановки получает значение k_i, то можно записать

,

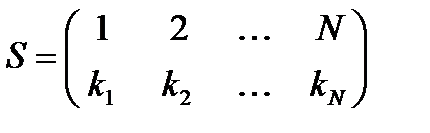где .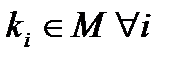

Очевидно, если последовательно применить две подстановки S₁ и S₂, то их результат снова будет подстановкой, равной композиции (произведению) исходных подстановок S = S₁ × S₂. Множество подстановок одинаковой степени образует группу относительно «умножения», определенного таким образом. Отсюда следует, что для каждой подстановки существует обратная операция. Нейтральным элементом группы подстановок служит тривиальная подстановка, оставляющая на месте все элементы множества.

Пусть открытый текст представляет собой фразу «открытый текст», а подстановка задана таблицей

.

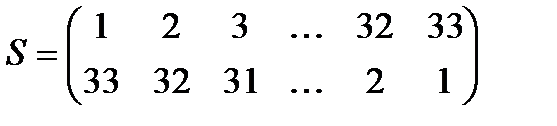Шифртекст имеет вид «тоцреоечаоыцпо». Очевидно, что ключом к этому шифру является сама подстановка S. Количество всевозможных подстановок для алфавита из N символов равно N!,что делает раскрытие ключа методом полного перебора проблематичным. На первый взгляд, криптостойкость такого шифра должна быть очень высокой. Однако недостатком шифра простой подстановки является то, что статистические свойства текста (частоты появления букв) при шифровании сохраняются, благодаря чему криптостойкость шифра на самом деле низка. Если в распоряжении дешифровальщика окажется достаточно длинный шифртекст (несколько десятков знаков), то шифр может быть взломан за несколько минут путем подсчета частот букв и сравнения с известными статистическими характеристиками русского (английского и т.д.) текста.