Общие понятия о цифровой обработке

Под обработкой сигналов в широком смысле можно понимать совокупность преобразований, направленную на наиболее эффективную передачу, хранение и извлечение информации. В последние десятилетия все более широко применяется цифровая обработка сигналов (ЦОС), которой свойственны следующие преимущества перед аналоговой обработкой:

– принципиальная возможность реализации практически любых алгоритмов обработки в реальном масштабе времени (возможности аналоговой техники значительно скромнее);

– потенциально сколь угодно высокая точность реализации алгоритмов, определяемая разрядностью цифровых устройств;

– возможность безошибочного воспроизведения сигналов при передаче и хранении на основе помехоустойчивого кодирования, которое применимо только к цифровым сигналам.

Преимущества цифровой обработки основываются на свойствах дискретных сигналов и цепей, которые во многом сходны с аналоговыми, но в то же время имеют и существенные особенности [7].

Под цифровым сигналом понимают дискретный сигнал, квантованный по уровню.

Математической моделью дискретного сигнала служит последовательность s[n] (дискретный аргумент принято заключать в квадратные скобки), где s – аргумент, принимающий значения из дискретного множества, а функция s[•] может принимать значения из непрерывного множества вещественных или комплексных чисел (в пространственно-временной обработке сигналов функция s[•] принимает векторные значения). В соответствии с теоремой отсчетов, аналоговый сигнал s(t) с финитным спектром, сосредоточенным в полосе частот (-F_в, F_в), может без потерь информации быть заменен дискретной последовательностью s[n] = s(nT_d) своих значений, взятых с шагом T_d < 1/2F_в, которая и представляет собой дискретный сигнал.

Таким образом, цифровой сигнал – это последовательность, принимающая значения из дискретного (как правило, конечного) множества. Это связано с тем, что цифровые устройства всегда имеют ограниченную разрядность и отсчеты сигналов, подлежащих цифровой обработке округляются (квантуются). Для изучения ряда вопросов цифровой обработки сигналов удобнее считать, что сигнал принимает значения из непрерывного множества, поэтому используется модель дискретного сигнала. Моделью цифрового сигнала пользуются в тех случаях, когда рассматриваются специфические эффекты, связанные с квантованием сигнала, округлением промежуточных результатов, ограничением разрядной сетки цифрового устройства и т.п.

Для последовательности (дискретного сигнала) s[n], где n принимает целые значения от -∞ до +∞ можно определить дискретное преобразование Фурье

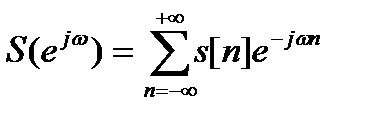, (11.1)

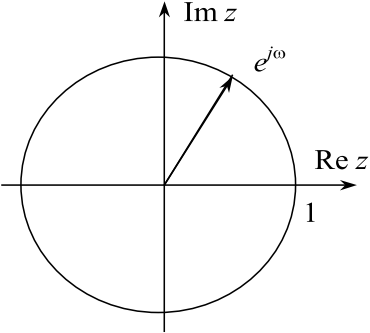Легко заметить, что изменение ω на величину ±k∙2π при любом целом k никак не влияет на результат преобразования. Таким образом, величину ω можно понимать, как угол, а e^jω – как точку на комплексной плоскости, находящуюся на окружности единичного радиуса (рис. 11.1). Поэтому выражение (11.1) определяет на единичной окружности функцию вещественной переменной ω, которая имеет смысл круговой частоты.

Рис. 11.1. Угловая интерпретация частоты

Вспомним, что при восстановлении аналогового сигнала моделью дискретного сигнала служит идеализированный АИМ-сигнал, состоящий из δ-функций, умноженных на отсчеты сигнала

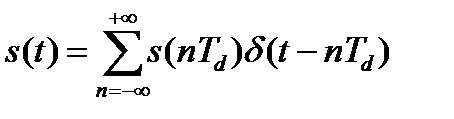
Преобразование Фурье этого аналогового сигнала, обозначив круговую частоту в его спектральном описании буквой Ω, находится как:

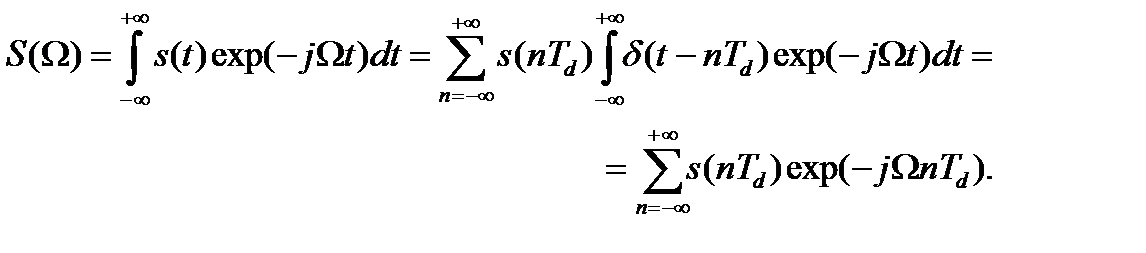(11.2)

Сравнивая выражения (11.1) и (11.2), легко увидеть, что при условии

s[n] = s(nT_d),

ω = ΩT_d, -π ≤ ω ≤ π (11.3)

их левые части совпадают. Это означает, что выражение (11.1) определяет спектральную плотность дискретного сигнала, совпадающую по форме со спектральной плотностью идеального АИМ-сигнала (который при воздействии на идеальный ФНЧ с П-образной характеристикой позволяет точно восстановить исходный аналоговый сигнал).

Из условия (11.3) следует необходимое ограничение -π/T_d ≤ Ω ≤ π/T_d, или, что то же самое, -Ω_d/2 ≤ Ω ≤ Ω_d/2, где Ω_d = 2πF_d = 2π/T_d – круговая частота дискретизации. Иными словами, мы снова получили условие выбора частоты дискретизации, как минимум, вдвое выше верхней частоты спектра аналогового сигнала.

Таким образом, при условии финитности и правильного выбора шага дискретизации, любые действия над дискретным сигналом эквивалентны соответствующим действиям над аналоговым сигналом и обработка сигнала может производиться в цифровой форме.

Рассмотрим выражение (11.1) как разложение 2π-периодической функции аргумента ω в комплексный ряд Фурье по базисным функциям exp(jnω), -∞ ≤ n ≤ ∞. Тогда, очевидно, отсчеты s[n] не что иное, как коэффициенты этого ряда и могут быть найдены по общей формуле для вычисления коэффициентов комплексного ряда Фурье:

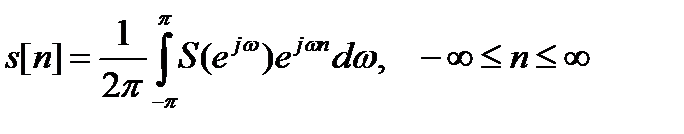, (11.4)

Это выражение представляет собой обратное преобразование Фурье для последовательности (дискретного сигнала).

Квантование сигнала

Операция квантования непрерывной величины состоит в том, что множество ее возможных значений заменяется определённым конечным числом значений. Существующие устройства квантования обычно осуществляют равномерное квантование сигналов, при котором границы интервалов квантования размещаются равномерно в заданном диапазоне значений сигнала, а значения уровней квантования располагаются посередине между этими границами. При равномерном квантовании количество порогов квантования оценивается величиной

r = (u_max - u_min)/∆u,

где u_max и u_min – максимальная и минимальная амплитуды дискретизируемого сигнала. Пороги квантования разбивают интервал (u_max - u_min) на (r + 1) подинтервалов – уровней квантования.

Отсчет непрерывного процесса в АЦП преобразуется в двоичный код из m разрядов, каждый из которых представлен нулем или единицей. Число разрядов определяется числом уровней квантования:

m = [log₂(r + 1)].

При обработке, когда требуется осуществлять цифровую фильтрацию сигналов и компенсацию помех, число уровней квантования нужно увеличивать, чтобы уменьшить по возможности искажения сигналов и помех. На практике часто выбирают ∆u = u_min ≈ σ_ш, где σ_ш² – дисперсия собственного шума приемника. При этом число порогов квантования равно r = d - 1, где d = u_max/σ_ш – динамический диапазон аналоговой части приемника. Отсюда получаем требуемое число разрядов кода и соответственно число разрядов АЦП:

m = [log₂d].

Следующий шаг в преобразовании сигнала состоит в переводе квантованного сигнала в цифровой сигнал. Эта операция называется кодированием сигнала.

Кодирование сигнала

Позиционность.Сначала рассмотрим одно замечательное свойство системы счисления – позиционность. Возьмем какое-нибудь число, например 777. В нем один и тот же знак «7» участвует 3 раза, но обозначает то семь единиц, то – в центре – семь десятков, а слева – семь сотен. Таким образом, при записи числа цифра может иметь одно начертание, а значения в зависимости от места (позиции), разряда, на котором она стоит, – разные. Такой принцип построения чисел называется позиционным. Для записи любых сколь угодно больших чисел достаточно десяти цифр.

Каждая позиция, или разряд, числа имеет определенный «вес» (единицы, десятки, сотни и т. д.), поэтому число 777 можно расписать как

777 = 7×10² + 7×10 + 7,

т.е. семь сотен плюс семь десятков плюс семь единиц.

Если вместо чисел записать буквы, то можно получить общую форму представления числа:

М = a_n×10ⁿ + a_n-1×10^n-1 + ... + a₁×10 + a₀

или сокращенную (опуская степени числа 10) – через коэффициенты:

М = (a_na_n-1 ... a₁a₀)

Число 10 является основанием системы счисления. Коэффициенты a₀ (число единиц), a₁ (число единиц второго разряда, т.е. десятков), a₂ (число единиц третьего разряда, т.е. сотен) и т.д. могут принимать значения, не превышающие основания системы: от 0 до 9.

Основанием системы счисления может быть любое целое число, т.е. число можно представить комбинацией степеней основания, например, 7:

М = a_n×7ⁿ + a_n-1×7^n-1 + ... + a₁×7 + a₀

Ясно, что значения коэффициентов a₀, a₁,...,a_n должны теперь быть не больше нового основания, т.е. 7: они могут принимать значения от 0 до 6.

Представим число 777 в семеричной системе, разлагая его по степеням основания 7:

(777)₁₀ = 2×7³ + 1×7² + 6×7.

Если опустить степени числа 7, как мы делаем при записи чисел в десятичной системе, то получим семеричную запись этого числа: (2160)₇. Здесь цифра 7 в индексе указывает основание системы.

В пятеричной позиционной системе всего пять цифр: 0, 1, 2, 3, 4. В ней число 777 будет представлено количеством «пятерок», «двадцатипяток» и т. д.:

(777)₁₀ = 1×5⁴ + 1×5³ + 1×5² + 0×5 + 2 = (11102)₅.

Посмотрим, как будет представлено число 777 в двенадцатеричной системе. Поскольку в ней должно быть двенадцать цифр, а мы знаем только десять, то придется ввести еще две цифры, обозначив 10, скажем, буквой A, а 11 – буквой B. В результате получим

(777)₁₀ = 5×12² + 4×12 + 9 = (549)₁₂.

Как видно, можно придумать много различных позиционных систем счисления, отличающихся только основаниями. И все они, вообще говоря, равнозначны: ни одна из них не имеет явных преимуществ перед другой.

Число 2 – это самое меньшее из чисел, которое можно взять за основание системы счисления. Поэтому в двоичной системе счисления всего две цифры: 0 и 1. Число в двоичной системе запишется так:

М = a_n×2ⁿ + a_n-1×2^n-1 + ... + a₁×2 + a₀.

Если в десятичной системе "вес" каждой позиции (или разряда) числа равен числу 10 в некоторой степени, то в двоичной системе вместо числа 10 используют число 2.

Запишем число (777)₁₀ в двоичной системе счисления, представляя его в виде разложения по степеням двойки и отбрасывая потом при записи сами степени:

(777)₁₀=1×2⁹ + 1×2⁸ + 0×2⁷ + 0×2⁶ + 0×2⁵ + 0×2⁴ + 1×2³ + 0×2² + 0×2 + 1 = = (1100001001)₂.

Итак, в двоичной системе счисления вместо числа 777 приходится писать число 1100001001.

При записи числа в двоичной системе каждая позиция занята двоичной цифрой. Вместо двух слов "двоичная цифра" употребляют одно слово: "бит", составленного из начальных и конечной букв словосочетания "binary digit", что в переводе с английского означает "двоичная цифра".

С помощью одного бита можно записать только числа 0 и 1, двух бит – числа от 0 до 3, трех бит – числа от 0 до 7, четырех бит – числа от 0 до 15 и т.д.

Десятичная запись

0 1 2 3 4 5 6 7 8 9 10 11 12 … 15 16

Двоичная запись

0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 … 1111 100000

Чтобы записать числа от 0 до 1000 в двоичной системе счисления потребуется десять бит, т.е. даже сравнительно небольшое число занимает много позиций.