Принципы частотной и фазовой (угловой) модуляции

При фазовой и частотной модуляции сигнал имеет постоянную амплитуду и может быть записан в следующем виде:

S_ФМ(ЧМ)(t) = U∙cos(φ(t)). (9.1)

В отсутствие модуляции аргумент гармонического колебания мгновенная (полная) фаза φ(t) = ω₀t изменяется с постоянной скоростью ω₀, т.е. является линейной функцией времени. И фазовая, и частотная модуляция предполагают зависимость изменения фазы φ(t) от информационного сигнала s_c(t). Эта общность позволяет объединить оба вида модуляции одним названием – угловая модуляция.

При угловой модуляции линейность изменения φ(t) нарушается и в каждый момент времени t скорость изменения φ(t) определяется мгновенной частотой ω(t), причем:

.

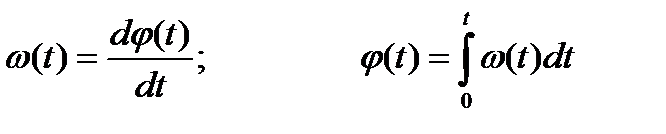Фазовая модуляция – процесс изменения мгновенной фазы несущего колебания пропорционально изменению непрерывного информационного сигнала:

φ(t) = ω₀t+ ∆φ(t) = ω₀t + a∙s_c(t) (9.2)

Таким образом

S_ФМ(t) = U_m∙cos[ω₀t + a∙s_c(t)]. (9.3)

Максимальное отклонение фазы называется индексом модуляции:

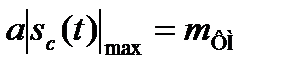. (9.4)

Если модуляция осуществляется гармоническим колебанием (тональная модуляция) s_c(t) = U_mΩ∙cosΩt с частотой Ω, то

S_ФМ(t) = U_m∙cos(ω₀t + a∙ U_mΩ ∙cosΩt) = U_m∙cos(ω₀t + m_ФМ∙cosΩt).

Заметим, что индекс модуляции m_ФМ = a∙ U_mΩ пропорционален амплитуде модулирующего колебания.

На рис. 9.1 показано, как изменяются мгновенная частота и фаза при тональной фазовой модуляции.

Информационный однотональный сигнал s_c(t) = U_mΩ∙cosΩt (рис. 9.1а) модулирует несущее колебание s_н(t) (рис. 9.1б), при этом закон изменения мгновенной фазы несущего колебания φ(t) = ω₀t + a∙s_c(t) повторяет закон изменения s_c(t) «косинус» (рис. 9.1в), т.е. на линейное изменение фазы (пунктир на рисунке) накладывается переменное приращение ∆φ(t) = a∙s_c(t), а закон изменения мгновенной частоты несущего колебания ω(t) (рис. 9.1г) определяется производной:

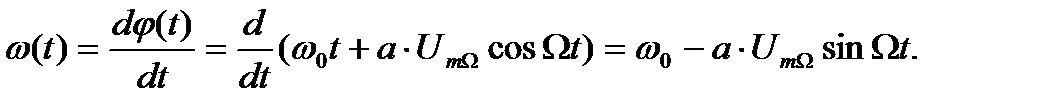
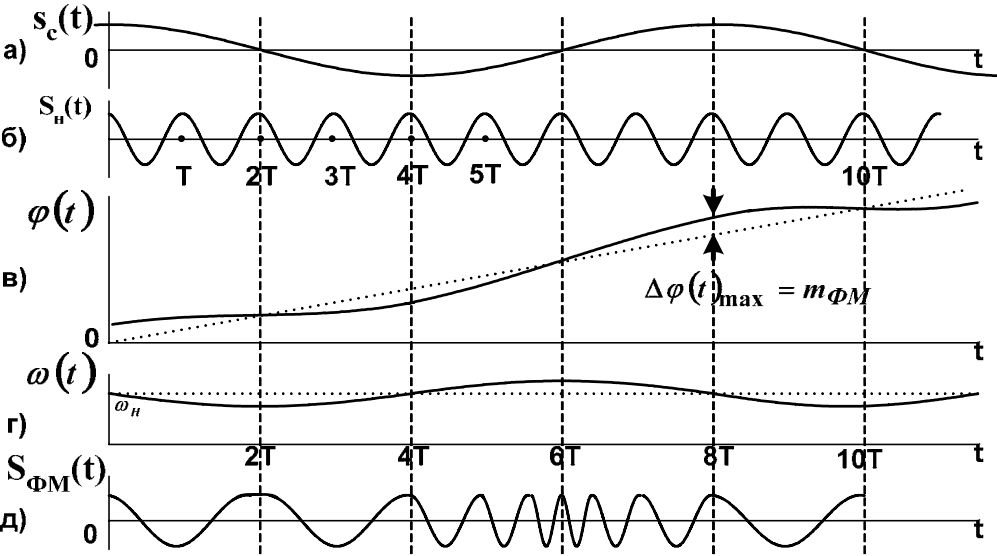
Рис. 9.1. Временные диаграммы процесса формирования ФМ сигналов

Фазомодулированное колебание (рис. 9.1д) построено на основании графика ω(t); в моменты времени t = 2Т и t = 10Т сигнал S_ФМ(t) имеет минимальную, а в момент t = 6Т максимальную мгновенную частоту.

Частотная модуляция – процесс изменения мгновенной частоты несущего колебания в соответствии с изменением информационного сигнала:

ω(t) = ω₀ + a∙s_c(t).

Рассмотрим наиболее простой способ однотональной частотной модуляции.

На рис. 9.2 изображены временные диаграммы изменения мгновенной частоты и фазы для однотональной частотной модуляции.

Информационный однотональный сигнал s_c(t) = U_mΩ∙cosΩt (рис. 9.2а) модулирует несущее колебание s_н(t) (рис. 9.2б), при этом закон изменения мгновенной частоты несущего колебания ω(t) = ω₀ + U_m∙a∙cosΩt повторяет закон изменения s_c(t) (рис. 9.2в). Здесь a∙U_mΩ = ∆ω_m – девиация частоты, пропорциональная амплитуде модулирующего колебания U_mΩ. Девиацией частоты называется максимальное отклонение частоты от среднего значения ω₀:

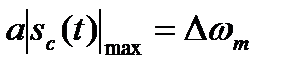. (9.5)

Отношение девиации частоты ∆ω_m к частоте модулирующего колебания Ω называется индексом частотной модуляции:

m_ЧМ = ∆ω_m /Ω. (9.6)

В моменты времени t = 0, t = 8Т мгновенная частота максимальна, в момент t = 4Т – минимальна. Закон изменения мгновенной фазы несущего колебания φ(t) (рис. 9.2г) определяется интегрированием

.

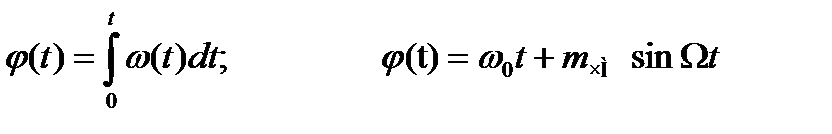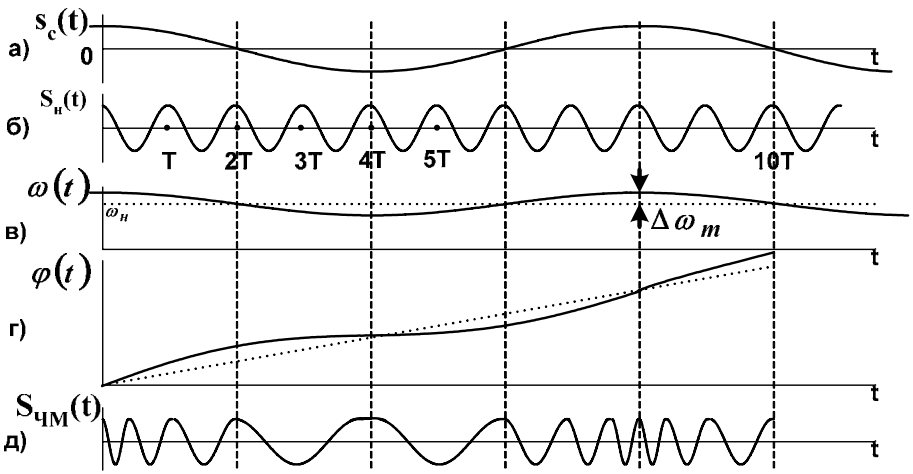
Рис. 9.2. Временные диаграммы процесса формирования ЧМ сигналов

Учитывая связь частоты и фазы, выражение для частотномодулированного сигнала запишется следующим образом:

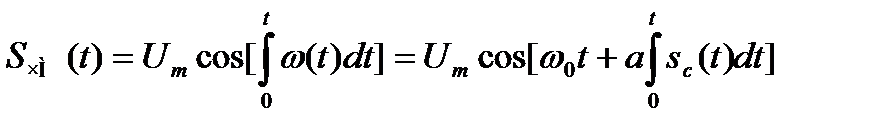. (9.7)

Для тональной частотной модуляции формула (2.14) принимает вид

S_ЧМ(t) = U_m∙cos(ω₀t + m_ЧМ∙ sinΩt). (9.8)

Сравнение выражений (9.3) и (9.7) показывает, что при ФМ приращение фазы пропорционально модулирующему колебанию s_c(t), а при ЧМ – интегралу от s_c(t). Если сначала проинтегрировать s_c(t), а затем этим колебанием модулировать несущую по фазе, то получится ЧМ сигнал. Такой способ формирования ЧМ сигнала имеет практическое применение. Подобным же образом, если продифференцировать s_c(t) и это колебание использовать для модуляции частоты, то получим ФМ сигнал.