Детерминированные конечные автоматы-распознаватели.

Определение. Конечный автомат-распознаватель А определяется как пятерка объектов: A={X, S, S_o, δ, F}, где Х – конечное не пустое множество символов входного алфавита; S – конечное непустое множество состояний автомата; S_oϵS – начальное состояние автомата; F S – множество заключительных (финальных) состояний. Функция переходов определяется так же, как и в схемотехнических конечных автоматах.

Определение. Конечный автомат-распознаватель называется детерминированным (ДКА), если из любого возможного состояния по любому допустимому входному сигналу возможен переход в точности в одно из состояний, т.е. ( sϵS) ( xϵX) (|δ(x,s)|=1). Другими словами, для ДКА значение функции переходов для любой пары {входной сигнал, состояние} является одновременное подмножество множества состояний. Поэтому функция переходов ДКА понимается не как отображение множества S×X в множество 2^S, а как отображение множества S×X, в само множество состояний S.

Определение. ДКА (X, S, S_o, δ, F) допускает входную цепочку xϵX, если x переводит его из начального в одно из заключительных (финальных) состояний, т.е. если δ(x,S_o)ϵF. Множество всех цепочек, допускаемых ДКА, образует язык, допускаемый ДКА.

Язык, допускаемый автоматом-распознавателем A={X, S, S_o, δ, F}, Обозначается как L_A. Очевидно, что L_A={xϵX|δ(x,s_o)ϵF}.

Определение. Язык, для которого существует распознающий его конечный автомат, называется автоматным языком.

Для задания конечных автоматов-распознавателей используются как таблицы переходов, так и графы переходов. Вершины графа переходов, соответствующие заключительные состояниям, выделяются двойным кружком.

Пример. Построить граф переходов автомата-распознавателя для языка L={abc,cc} при алфавите V={a,b,c} (рис5.2. ).

Рис. 5.2. Граф переходов автомата-распознавателя.

Входные цепочка abc и cc (и только они) переводят автомат из начального состояния S_o в одно из заключительных состояний S₃ и S₅.

Здесь и далее будем считать, что если переход автомата под воздействием некоторого символа х не определен в состоянии S, то это по умолчаю означает, что существует незаключительное состояние, в которое этот автомат переходит из состояния S под воздействием символа x, при чем при воздействии любых других цепочек, автомат не выходит из этого незаключительного состояния. Это означает, что входной символ х в состоянии автомата s не допускается. В частности в рассматриваемом примере автомата-распознавателя в заданном языке нет цепочек, начинающихся с символа b, поэтому символ b в состоянии автомата S_o запрещен.

Пример. Построить граф переходов автомата-распознавателя А, для которого допустимым является язык L={X, X – содержит конечное четное число нулей и конечное четное число 1}.

ДКА ведет подсчет 0 и 1путем суммирования по mod 2. Таким образом, автомат запоминает число 0 и 1поданых на его вход. Следовательно, автомат имеет всего четыре возможных состояния:

1. Прочитано четное число нулей и четное число едениц;

2. Прочитано четное число нулей и нечетное число едениц;

3. Прочитано нечетное число нулей и четное число едениц;

4. Прочитано нечетное число нулей и нечетное число едениц – S₃.

Граф состояний ДКА, распознающего заданный язык L, представлен на рис 5.3

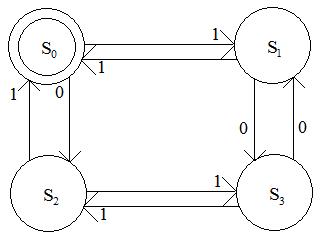
Рис. 5.3. Граф перехода автомата, распознающего язык L={X}.

В связи с тем, что ноль является числом четным, состояние S_o будет начальным, т.к. до того, как на автомат поступят какие-либо входные данные, их количество равнялось нулю. По графу переходов видно, что это же состояние S_o является и финальным, т.к. оно единственное в точности фиксирубщее все последовательности 0 и 1, принадлежащих языку L.

В теории формальных языков большое значение имеют утверждения, в которых формулируются необходимые условия принадлежности языка к автоматным языкам. Чаще всего доказывается, что тот или иной язык не является автоматным, а, следовательно, не требуется искать для него соответствующую грамматику. Такой подход объясняется тем, что доказательство принадлежности языка к классу автоматных языков значительно труднее, т.к. требуется сформулировать грамматику, порождающую данный язык.

Отметим, что в теории формальных языков и автоматов-распознавателей часто используется принцип Дирихле. Этот принцип гласит: пусть задана функция f:A→B и мощность множества |A|=n, а мощность множества |B|=m, (n>m)ϵN. Тогда некоторое свое значение функция f примет, по крайней мере, (n+1) раз.

В англоязычной литературе принцип Дирихле трактуется как принцип «голубятни», который представляется следующим образом: Если n голубей разместить в m клетках при n>m, то хотя бы в одной клетке окажется больше одного голубя.

Рассмотрим пример. V={0,1}, L={0ⁿ,1ⁿ|nϵN}, т.е. этот язык состоит из цепочек вида 01, 0011, 000111 и т.д. Утверждается, что язык L не является автоматным.

Пусть автомат имеет К состояний (К>1). Предположим, что на вход автомата поступило К нулей. После прочтения (К+1) префиксов цепочки автомат находится в некотором состоянии. Поскольку у автомата только К состояний, то согласно принципу Дирихле, прочитав два различных префикса, например 0ⁱ и 0^j (i≠j), автомат будет находится в одном из том же состоянии S_n. После окончания префикса, состоящего из i или j нулей, на вход автомата поступает последовательность единиц. Прочитав i единиц, автоматдолжен перейти в финальное состояние, если на его вход было подано i нулей, а если на его вход было подано j нулей, то он должен перейти в одно из незаключительных состояний. Но так как при прочтении i или j нулей автомат находится в одном и том же состоянии, то он не может определить принадлежит ли поступившая на вход цепочка к заданному языку или нет.

В рассмотренном примере показано, что язык L={0ⁿ, 1ⁿ|n>1} не является автоматным, из чего следует, что не все языки представими конечными автоматами.

Важным теоретическим результатом, позволяющим определить принадлежность рассматриваемого языка к классу автоматных, является лемма о накачке.

Лемма о накачке. Пусть L – автоматный язык над алфавитом V. Тогда

( nϵN)( aϵL:|a|≥n) ( u,ν,ωϵV*):

[a=uνω&|uν|≤n&|ν|≥1&( iϵN)(uνⁱωϵL)].

Другими словами, если L автоматный язык, то существует константа n, для которой каждую цепочку a из языка L, удовлетворяющую неравенству |a|≥n, можно разбить на три цепочки a=uνω так, что выполняются следующие условия:

1. ν≠ε,

2. |uν|≤n

3. Для любого i≥0, цепочка a=uνⁱω так же принадлежит языку L.

Условие 3 говорит о том, что в цепочке a=uνⁱω всегда можно выделить цепочку ν, которую можно «накачать» i раз. То есть, если цепочку ν повторить любое число раз или удалить ее (i=0), то результирующая цепочка все равно будет принадлежать языку L.

Поскольку язык L автоматный, то существует конечный автоматраспознающий этот язык A={ X, S, S_o, δ, F}. Введем константу К определяемую как число сопоставлений автомата A (K=|S|). Зафиксируем цепочку aϵL, длина которой не меньше К. Так как n>0, то цепочка а не является пустой и эту цепочку можно записать в виде a=a₁a₂…a_n, n>0.

В связи с тем, что мы рассматриваем детерминированные автоматы, то существует единственный путь, ведущий из начального состояния S_o в одно из финальных состояний S_f, на котором будет прочитана цепочка а (рис.5.4).

Рис. 5.4. Граф переходов автомата А при чтении цепочки а.

Так как длина цепочки а не меньше числа состояний автомата А, т.е. числа всех вершин графа переходов этого автомата, и так как число вершин в любом пути на графе на единицу больше числа дуг на этом пути, то число вершин на рассматриваемом пути будет больше, чем число всех вершин графа. Это значит, что хотя бы одна из вершин данного пути повторяется и она, следовательно, включена в некоторый контур. Обозначим эту вершину S_p. Тогда путь для цепочки а разбивается на три части (рис.5.5):1. Путь из S_o в S_p, 2. контур, проходящий через S_p, 3. путь из S_p в S_f.

Рис.5.5 Граф переходов автомата А с учетом возможного контура.

Обозначив через u цепочку, читаемую на первой части пути, через ν-цепочку, читаемую в контуре u через ω-цепочку, читаемую на третьей части получим а=uνω. Отметим, что так как любой контур есть простой путь, то |ν|≤n (длина простого пути не может быть больше, чем число вершин графа) и ν≠ε, т.к. контур имеет не нулевую длину. Из сказанного следует, что контур, включенный в вершину S_p, можно пройти любое число i раз (i≥0) или ни разу. В первом случае на этом пути будет прочитана цепочка uνⁱω при i>0, а во втором случае при i=0 – цепочка uω. Таким образом, любая цепочка a= uνⁱω (i≥0) принадлежит языку L.