Введение в общую теорию конечных автоматов.
ВВЕДЕНИЕ В ОБЩУЮ ТЕОРИЮ КОНЕЧНЫХ АВТОМАТОВ.
СОДЕРЖАНИЕ
Раздел1 Основы алгебры логики 1- 20
Раздел2.. Минимизация булевых функций 20-33.
Теория и практическое применение 33-46.
Контрольные задания 46-47.
Раздел3. Конечные автоматы 48- 71
Раздел4. Проблемы синтеза и гонок 72- 80
Раздел 5.Конечноавтоматные преобразования, языки и грамматики80-90
Контрольные задания 91
Литература. 93
Раздел 1. Основы алгебры логики.
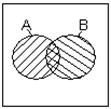
Диаграммы Венна.
Наглядная интерпретация основных соотношений булевых переменных представлена на диаграммах Венна.
Класс булевых переменных определяется как класс, включающий все области внутри квадрата (рис.1.1).

рис.1.1
Любой элемент А этого класса представлен областью, ограниченной замкнутой кривой. 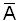 - совокупность точек квадрата, не входящих в область А.
- совокупность точек квадрата, не входящих в область А.
Здесь 0 представлен как класс, совсем не имеющий точек, а 1 – как класс всех точек квадрата.
А+В – наименьшая область, содержащая одновременно А и В.
АВ – наибольшая область, содержащаяся одновременно и в А, и в В. Диаграм-мы Венна для элементарных булевых функций изображены на рис.1.2:
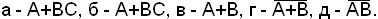
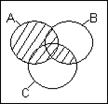
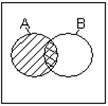
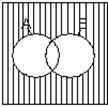
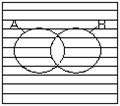
а) б) в) г) д) рис.1.2
Формы записи булевых функций.
Табличная запись.
Одним из распространенных способов записи булевой функции является ее задание с помощью таблицы соответствия (таблицы истинности), которая сопоставляет всем двоичным наборам аргументов значения функции на этих наборах. Буквы и наборы в таблице могут располагаться в любом порядке, однако практически целесообразно осуществлять запись следующим образом:
1) порядок записи букв в таблице совпадает с порядком аргументов в записи функции;
2) наборы, представляющие собой двоичные числа, располагаются в таблице в порядке их возрастания. Каждому набору приписывается номер соответственно представляемому им числу:
000…00 – нулевой набор;
000 …01 – 1-й набор;
. . . . . . . . . . . . . . . . . . .
111 … 11 - (2n-1)–й набор.
Функция, записанная в табличном виде, имеет индекс, равный двоичному числу, образованному значениями этой функции, записанными слева направо, начиная со значения на нулевом наборе.
Пример. Запись функции f248(АВС) = 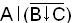 приведена в табл.1.5
приведена в табл.1.5
Таблица 1.5
 |
A B C B↓C 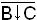
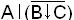
 |
0 0 0 1 0 1
0 0 1 0 1 1
0 1 0 0 1 1
0 1 1 0 1 1
1 0 0 1 0 1
1 0 1 0 1 0
1 1 0 0 1 0
1 1 1 0 1 0
При задании булевых функций при 3≤n≤10 иногда используют прямоугольные таблицы, т.е. те же таблицы соответствия, но в несколько ином начертании, позволяющем получить более компактную запись. Для функции от n переменных такая таблица имеет 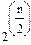 строк и
строк и 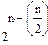 столбцов, где
столбцов, где 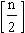 - целая часть числа n/2.
- целая часть числа n/2.
Пример. Запись функции f(ABCD)=[(C→D)~B] 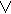 [A |0] дана в табл.1.6
[A |0] дана в табл.1.6
Пример. Запись функции f(ABCD)= 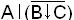 приведена в табл.1.7
приведена в табл.1.7
Таблица 1.6 Таблица 1.7
 |  | ||
CD BC




 А
А

 AB 00 01 10 11 00 01 10 11
AB 00 01 10 11 00 01 10 11
00 1 1 1 1 0 1 1 1 1
01 1 1 1 1 1 1 0 0 0
10 0 0 1 0
11 1 1 0 1
Аналитическая запись.
Произведение булевых переменных называется булевым произведением. Булево произведение называется элементарным, если переменные в него входят только один раз в прямой или инверсной форме.
Пример. 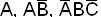 - элементарные произведения,
- элементарные произведения, 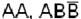 - эти произведения не являются элементарными.
- эти произведения не являются элементарными.
Число переменных, образующих элементарное произведение, называется длиной или рангом элементарного произведения.
Пример. 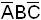 - ранг 3.
- ранг 3.
Минтермом или конституентой единицы n переменных называется элементарное произведение ранга n.
Аналогичные определения существует и для булевых сумм.
Пример. 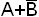 - элементарная сумма ранга 2;
- элементарная сумма ранга 2; 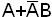 не является элементарной суммой.
не является элементарной суммой.
Макстермом или конституентой нуля n переменных называется элементарная булева сумма ранга n.
Как булева функция минтерм принимает значение единицы только на одном наборе, аналогично макстерм принимает только на одном наборе значение нуля.
При записи минтерма часто используется буква m с индексом того набора, на котором данный минтерм принимает значение единицы.
Пример. 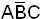 =m5.
=m5.
Двоичный эквивалент индекса для минтерма может быть определен из записи минтерма подстановкой вместо прямых форм переменных цифры 1, а вместо инверсных – цифры 0.
Пример. 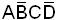 - минтерм ранга 4;
- минтерм ранга 4;
1010 – двоичный эквивалент индекса.
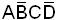 = m10.
= m10.
При этом не следует забывать, что при переходе от индексной записи минтерма к аналитической следует восстановить все переменные, входящие в данную запись.
Пример. m5 – ранга 4 имеет запись 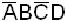 ; m5 – ранга 3 имеет запись
; m5 – ранга 3 имеет запись 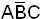 .
.
Аналогично при записи макстерма используется буква М с индексом, двоичная запись которого содержит 1, если соответствующая переменная входит в аналитическую запись макстерма в прямой форме, и 0, если в инверсной.
Пример. 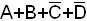 =М1100= М12.
=М1100= М12.
Между минтермами и макстермами существует следующая связь:
 i = M2n-i-1;
i = M2n-i-1;  i = m2n-i-1.
i = m2n-i-1.
Булева сумма всех минтермов ранга n равна единице:
2n-1
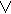 mi =1.
mi =1.
i=0
Это следует из того, что число различных минтермов ранга n равно 2n, т.е. числу различных наборов n переменных, а функция, принимающая на всех наборах значение 1, есть константа 1.
Используя теорему де Моргана, можно показать, что произведение всех макстермов ранга n равно нулю:
2n-1
Λ Mi =0.
i=0
Из этих уравнений следует
mimj =0 при i≠j;
Mi + Mj =1 при i≠j.
Равенства очевидны, если вспомнить, что минтерм – это конституента единицы, а макстерм – конституента нуля.
Основная теорема.
Любая булева функция может быть выражена булевой суммой минтермов или произведением макстермов.
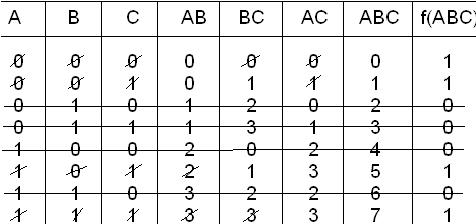
Таблица 1.8 Составим таблицу функций и найдем булево



 A B C f(ABC) выражение для данной функции. Из табл.1.8 видно,
A B C f(ABC) выражение для данной функции. Из табл.1.8 видно,
 0 0 0 0= α0 что функция равна единице, только на наборах,
0 0 0 0= α0 что функция равна единице, только на наборах,
0 0 1 1= α1 равных 001, 101, 111, что соответствует минтер-
0 1 0 0= α2 мам 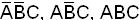 .
.
0 1 1 0= α3 Это значит, что данная функция может быть
1 0 0 0= α4 дизъюнкцией этих минтермов, т.е.
1 0 1 1= α5 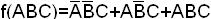 = m1 + m5+ m7.
= m1 + m5+ m7.
1 1 0 0= α6 Чтобы убедиться в сказанном, запишем дан-
1 1 1 1= α7 ную функцию в виде суммы произведений значений функции на соответствующие минтермы:
f(ABC)= α0 m0 + α1 m1 + α2 m2 + α3 m3 + α4 m4 + α5 m5 + α6 m6 + α7 m7 =
= 0m0 + 1m1 + 0m2 + 0m3 + 0m4 + 1m5 + 0m6 + 1m7 ,
где αi – значение данной функции на i –ом наборе.
Следовательно, справедлива запись:
2n-1
f(x1 x2 … xn)= 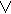 α i mi .
α i mi .
i=0
Применив формулу де Моргана, найдем выражение
2n-1
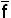 ( x1 x2 … xn)=
( x1 x2 … xn)= 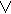
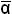 i mi .
i mi .
i=0
 2n-1 2n-1 2n-1 2n-1
2n-1 2n-1 2n-1 2n-1
 f(x1 x2 … xn)=
f(x1 x2 … xn)= 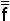 (x1 x2 … xn)=
(x1 x2 … xn)= 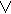
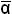 i mi = Λ (
i mi = Λ ( 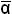 i mi)= Λ (α i +
i mi)= Λ (α i + 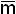 i)= Λ (α i +M2n-i-1).
i)= Λ (α i +M2n-i-1).
i=0 i=0 i=0 i=0
Основная теорема:
2n-1 2n-1
f(x1 x2 … xn)= 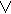 α i mi = Λ (α i +M2n-i-1).
α i mi = Λ (α i +M2n-i-1).
i=0 i=0
Для аналитических записей булевых функций существуют следующие определения:
Булева сумма элементарных произведений называется дизъюнктивной нормальной формой (ДНФ).
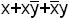 - ДНФ;
- ДНФ;
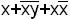 - не является ДНФ.
- не является ДНФ.
Булево произведение элементарных сумм называется конъюнктивной нормальной формой (КНФ).
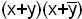 - КНФ;
- КНФ;
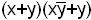 -не является КНФ.
-не является КНФ.
ДНФ функции n переменных, состоящая из элементарных произведений ранга n (т.е. из минтермов), называется совершенной дизъюнктивной нормальной формой функции (СДНФ).
КНФ функции n переменных, состоящая из элементарных сумм ранга n (т.е. из макстермов), называется совершенной конъюнктивной нормальной формой функции (СКНФ).
Основная теорема содержит запись СДНФ и СКНФ функций.
Из теоремы следует, что запись СДНФ (или СКНФ) булевой функции единственна.
Выражение функции в СДНФ и СКНФ с помощью аналитических преобразований.
Для получения СДНФ функции аналитическим способом используется следующий прием:
1) аналитическое выражение функции приводится к бесскобочной записи в форме дизъюнкции каких-либо конъюнкций;
2) каждая конъюнкция, имеющая число сомножителей меньше n, умножается на выражение «1» через все недостающие переменные ( 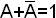 );
);
3) раскрываются скобки и приводятся подобные члены.
Пример. Найти СДНФ функции f(ABCD)= 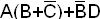 .
.
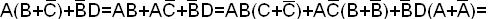
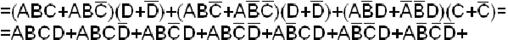
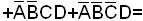 m15 + m14 + m13 + m12 + m11 + m9 + m8 + m3 +m1.
m15 + m14 + m13 + m12 + m11 + m9 + m8 + m3 +m1.
Для получения СКНФ функции без использования табличной записи следует применять процедуру вида:
1) аналитическое выражение функции приводится с помощью соотношения AB+C=(A+C)(B+C) к конъюнктивной записи со скобками, причем в скобках должны стоять дизъюнкции отдельных переменных в прямой или инверсной форме;
2) к каждой дизъюнкции добавляется выражение 0 через все недостающие переменные ( 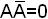 );
);
3) вновь используется дистрибутивный закон вида и приводятся подобные члены.
Пример. Найти СКНФ функции 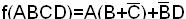
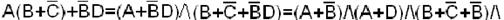
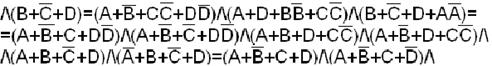
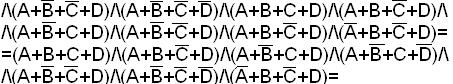
=М15 М13 М11 М10 М9 М8 М5
Рассмотрим расширение сокращенной записи элементарного произведения до суммы минтермов.
Пусть 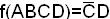 , представим данную запись в виде
, представим данную запись в виде
A B C D
- - 0 1
Затем, не меняя значений известных цифр в записи индекса минтерма, подставляем все возможные комбинации цифр соответствующих разрядов:
0 0 0 1
0 1 0 1
1 0 0 1
1 1 0 1
Полученные цифры соответствуют индексам минтермов, содержащихся в СДНФ исходной функции, т.е.
f(ABCD)=m1+m5+m9+m13.
Алгоритм построения.
Чтобы булеву функцию, заданную таблицей значений или любым другим способом, представить в виде многочлена, достаточно:
1) записать функцию в виде суммы по mod 2 минтермов, равных единице на тех же наборах, на которых равна заданная функция;
2) все аргументы, входящие в полученное выражение в инверсной форме, заменить с помощью соотношения 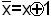 ;
;
3) раскрыть скобки и сделать приведение подобных членов с учетом тождества:
 x, если n нечетно;
x, если n нечетно;
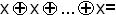
 0, если n четно.
0, если n четно.
n
Пример. Представить в виде многочлена функцию f14(AB):
f7(AB)= m0+m1+m2= m0 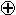 m1
m1 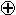 m2=
m2= 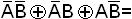
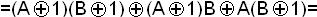
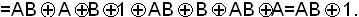
Пример. Представить в виде многочлена функцию f9(AB):
f9(AB)= m0+m3= m0 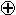 m3=
m3= 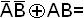
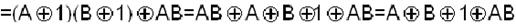 .
.
На базе функции 1, /\ и 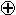 строится алгебра Жегалкина, но по своим свойствам она более близка к обычной алгебре и отличается от последней лишь тем, что логическое сложение заменено сложением по mod 2.
строится алгебра Жегалкина, но по своим свойствам она более близка к обычной алгебре и отличается от последней лишь тем, что логическое сложение заменено сложением по mod 2.
Метод Квайна.
Этот метод используется для получения сокращенной ДНФ функции из СДНФ ее с помощью операций неполного склеивания:
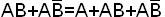
и поглощения A+AB=A.
Теорема Квайна. Если в СДНФ булевой функции провести все операции неполного склеивания, а затем все операции поглощения, то получится сокращенная ДНФ этой функции, т.е. дизъюнкция всех ее простых импликант.
Доказательство теоремы проверять не будем.
Чтобы получить все простые импликанты, так как один и тот же член дизъюнктивной формы может склеиваться с несколькими другими, образуя при этом различные импликанты, после склеивания исходный член следует сохранить.
Алгоритм метода Квайна.
1) Провести все возможные склеивания минтермов, входящих в СДНФ функции. В результате образуются элементарные конъюнкции ранга (n-1).
2) Так как склеиваться могут только элементарные конъюнкции одного ранга, то в дальнейших склеиваниях минтермы не участвуют, поэтому следует выполнить операции поглощения.
3) Над полученными элементарными конъюнкциями ранга (n-1) повторить операции склеивания и поглощения, образовав элементарные конъюнкции нижнего ранга, и т.д.
4) Процесс заканчивается, когда дальнейшее склеивание оказывается невозможным.
5) Оставшиеся в результате поглощения элементарные конъюнкции являются простыми импликантами функции, а дизъюнкция их есть сокращенная ДНФ функции.
Пример. Найти сокращенную ДНФ функции:

СДНФ функции
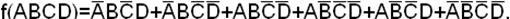
Приводим алгоритм метода:

Здесь \/ - отметка поглощения.
Сокращенная ДНФ функции:
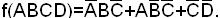
Пример. Найти сокращенную ДНФ функции:
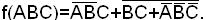
СДНФ функции
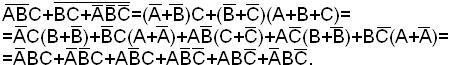
Проводим операции склеивания и поглощения:

Сокращенная ДНФ функции
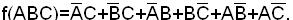
Гарвардский метод.
Метод, разработанный в Гарвардском университете, позволяет находить сокращенную ДНФ функции с использованием специальных карт для записи булевых функций соответствующего числа переменных.
В столбцах карт перечислены все элементарные конъюнкции функции n переменных, содержащие от 1-й до n букв.
Алгоритм Гарвардского метода.
1) Внести в карту для функции соответствующего числа переменных значения функции на всех наборах.
2) Вычеркнуть все строки, где записаны нулевые значения функции.
3) В каждом столбце таблицы вычеркнуть числа, совпадающие с числами в вычеркнутых строках данного столбца.
4) Из каждой не вычеркнутой строки выбрать элементарную конъюнкцию, содержащую наименьшее количество букв двоичный эквивалент которой остался не зачеркнутым.
Пример. Найти сокращенную ДНФ функции:
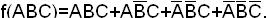
Карта для заданной функции приведена в табл.1.17.
В результате получаем
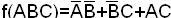 .
.
Нетрудно убедиться, что в полученной сокращенной ДНФ импликанту 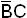 можно исключить:
можно исключить:
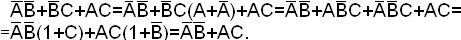
Таблица 1.17.
Простая импликанта, которую нельзя исключить из сокращенной ДНФ функции, называется существенной импликантой.
Дизъюнкция существенных импликант функции называется тупиковой ДНФ заданной функции.
Некоторые булевы функции имеют несколько тупиковых форм. Тупиковая ДНФ функции называется минимальной (МДНФ), если количество букв, которое она содержит, будет не больше, чем в любой другой ДНФ той же функции.
Отсюда следует, что для отыскания минимальных форм достаточно получить все тупиковые формы заданной функции и выбрать среди них минимальные.
Метод импликантных матриц.
Рассмотрим графический метод отыскания тупиковых форм функции из сокращенной ДНФ.
Импликантная матрица представляет собой таблицу, столбцы которой соответствуют всем конституентам единицы СДНФ заданной функции, а строки – всем простым импликантам.
В таблице по строке каждой импликанты отмечаются те минтермы, которые ею поглощаются.
Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число импликант, которые совместно накрывают все столбы импликантной матрицы, если в каком-либо из столбцов составленной импликантной матрицы функции имеется только одна отметка, то соответствующая ей импликанта является обязательной и обязательно входит в тупиковую форму функции, так как без нее будет получено накрытие всего множества минтермов.
Для случая  имеем импликантную матрицу, представленную в табл.1.18.
имеем импликантную матрицу, представленную в табл.1.18.
В данном случае импликанты AC и 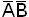 являются обязательными. Их сумма покрывает все минтермы, следовательно, тупиковая форма
являются обязательными. Их сумма покрывает все минтермы, следовательно, тупиковая форма 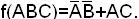 Она единственна и поэтому является минимальной.
Она единственна и поэтому является минимальной.
Таблица 1.18.
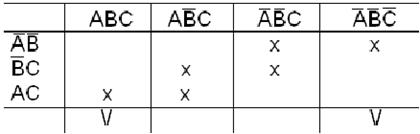
Пример. Найти минимальную ДНФ функции, используя метод Квайна и метод импликантных матриц:


Сокращенная ДНФ
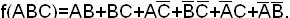
Импликантная матрица функции дана в табл.1.19.
Таблица 1.19
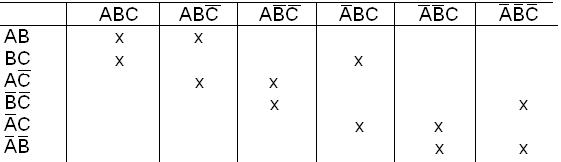
Так как нет столбцов с одной отметкой, то ни одна из импликант не является обязательной. Найдем минимальное количество простых импликант, накрывающее все колонки.
Возможны две тупиковые формы функции:
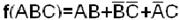 ;
;
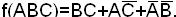
Обе формы содержат одинаковое число букв и, следовательно, обе являются минимальными.
Возможны другие тупиковые формы данной функции, но они не минимальны:
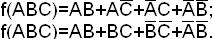
Метод Блека-Порецкого.
Используется для получения сокращенной ДНФ из любой произвольной функции представления [5].
Идея построения сокращенной ДНФ по произвольной ДНФ вытекает из следующего определения: если в ДНФ для данной функции f(x1 … xn) входит две конъюнкции вида Axi и Bxi, то имеет место равенство D=D\/AB, где D – ДНФ, эквивалентная функция f.
Алгоритм метода Блека-Порецкого.
1. Провести все возможные склеивания любых двух смежных термов, представляющих соответствующие элементарные конъюнкции, получить L-разрядный троичный набор и построить матрицу ранга n.
2. Над полученными элементарными конъюнкциями ранга (n-1) провести операции склеивания и поглощения, образовать элементарные конъюнкции нижнего ранга и т.д.
3. Процесс закончить, когда после операции склеивания и поглощения окажется, что в ДНФ отсутствуют члены, дальнейшее поглощение которых невозможно, т.е. когда будет получена сокращенная ДНФ.
4. Строится импликантная матрица и определяется максимальное покрытие.
Метод удобен при машинных способах минимизации.
Пример. Найти минимальную форму для заданной функции:
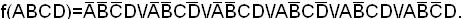
1. Матрица исходных данных 3. Матрица ранга (n-2)
0 0 0 1 2 0 2 1
0 0 1 0 2 0 2 1
0 0 1 1 2 0 1 2
1 0 0 1 2 0 1 2
1 0 1 0
1 0 1 1
2. Матрица ранга (n-1)*
0 0 2 1
2 0 0 1
0 0 1 2
2 0 1 0
2 0 1 1
1 0 2 1
1 0 1 2
4. Вычеркиваем одинаковые строки матрицы ранга (n-2) и получаем
A B C D
2 0 2 1
2 0 1 2
5. 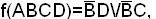
где 0 – инверсия переменной, 1 – переменная, 2 – отсутствует переменная.
Синтез конечных автоматов.
Синтез конечного автомата условно можно разделить на два этапа: абстрактный и структурный синтезы.
На этапе абстрактного синтеза выявляют факты изоморфизма автомата, определяют эквивалентные состояния, минимизируют заданный автомат по критерию числа состояний. Вопросы абстрактного синтеза были рассмотрены в предыдущей главе.
На этапе структурного синтеза рассматриваются вопросы элеиентарной базы, на которой происходит синтез заданного автомата, кодирование внутренних состояний автомата, кодирование внутренних состояний и некоторые другие вопросы реализации автоматов.
Наибольшее внимание при структурном синтезе уделяется выбору элементной базе для реализации автомата. В этом смысле задача структурного синтеза конечного автомата заключается в реализации сложного автомата из более простых, называемых элементарными автоматами.
ЛИТЕРАТУРА
1. Чирков М.К. Основы общей теории конечных автоматов. Л.: Издат. Ленинградского Университета. 1975., 280 стр.
2. Митюшин Ф.Ф., Нагорнова В.Ф., Шаповалов Ю.В. Теория, расчет и проектирование вычислительных устройств дискретного действия. Логическое проектирование. М.: МАИ, 1973., 176стр.
3. Белоусов А.И., Ткачев О.А. Дискретная математика. М.: Издат.МГТУ им. Н.Э.Баумана, 2004.,704стр.
4. Карпов Ю.Г. Теория автоматов. Спб.: Питер, 2002., 224стр.
5. Яблонский С.В., Гаврилов Г.П., Кудрявцев В.Б. Функции алгебры логики и классы Поста. М.: Наука, 1966. 120стр.
6. Митюшин Ф.Ф., Нагорнова В.Ф., Шаповалов Ю.В. Сборник задач по вычислительной технике. Арифметические и логические основы ЦВМ. М., МАИ, 1968. 112стр.
7. Каган Б.М. Электронные вычислительные машины и системы. М.: Энергоатомиздат. 1985. 552стр.
8. Палий И.А. Дискретная математика. Курс лекций. М.:Эксмо. 2008. 352стр.
9. Гилл А. Введение в теория конечных автоматов. М.: Наука. 1966. 272стр.
10. Левин В.И. Динамика логических устройств и систем. М.: Энергия. 1980. 224стр.
11. Фридман А., Менон П. Теория и проектирование переключательных схем. М.: Мир. 1978. 581стр.
12. Миллер Р. Теория переключательных схем. Том II. М.: Наука. 1971. 304стр.
13. Хопкрофт Дж. Мотвани Р., Ульман Джер. Введение в теорию автоматов, языков и вычислений. 2-е изд. М.: издательский дом «Вильямс». 2002. 528стр.: ил.
14. Куликов В.В. Дискретная математика. М.: РИОР. 2012. 174стр.
15. Клини С.К. Представление событий в нервных сетях (сб. «Автоматы». – м.: ИЛ, 1956. – с. 15-67.
[V1]
ВВЕДЕНИЕ В ОБЩУЮ ТЕОРИЮ КОНЕЧНЫХ АВТОМАТОВ.
СОДЕРЖАНИЕ
Раздел1 Основы алгебры логики 1- 20
Раздел2.. Минимизация булевых функций 20-33.
Теория и практическое применение 33-46.
Контрольные задания 46-47.
Раздел3. Конечные автоматы 48- 71
Раздел4. Проблемы синтеза и гонок 72- 80
Раздел 5.Конечноавтоматные преобразования, языки и грамматики80-90
Контрольные задания 91
Литература. 93
Раздел 1. Основы алгебры логики.
