Минимизация с использованием карт Карно

1. В карте Карно группы единиц (для получения ДНФ) и группы нулей (для получения КНФ) необходимо обвести четырехугольными контурами. Внутри контура должны находится только одноименные значения функции. Этот процесс соответствует операции склеивания или нахождения импликант данной функции.

2. Количество клеток внутри контура должно быть целой степенью двойки (1, 2, 4, 8, 16...).

3. При проведении контуров крайние строки карты (верхние и нижние, левые и правые), а также угловые клетки, считаются соседними (для карт до 4-х переменных).

4. Каждый контур должен включать максимально возможное количество клеток. В этом случае он будет соответствовать простой импликанте.

5. Все единицы (нули) в карте (даже одиночные) должны быть охвачены контурами. Любая единица (нуль) может входить в контуры произвольное количество раз.

6. Множество контуров, покрывающих все 1 (0) функции образуют тупиковую ДНФ (КНФ). Целью минимизации является нахождение минимальной из множества тупиковых форм.

7. В элементарной конъюнкции (дизъюнкции), которая соответствует одному контуру, остаются только те переменные, значение которых не изменяется внутри обведенного контура. Переменные булевой функции входят в элементарную конъюнкцию (для значений функции 1) без инверсии, если их значение на соответствующих координатах равно 1 и с инверсией - если 0. Для значений булевой функции, равных 0, записываются элементарные дизъюнкции, куда переменные входят без инверсии, если их значение на соответствующих координатах равно 0 и с инверсией - если 1.

В методе минимизирующих карт Карно функция задается прямоугольной таблицей, в которой наборы значений переменных на каждой из сторон прямоугольника расположены в коде Грея. Нахождение простых импликант сводится к выделению максимальных по включению прямоугольников, состоящих из единиц. Из прямоугольников, соответствующих граням максимальной размерности, находим коды максимальных интервалов. Считается, что каждая клетка таблицы является соседней к клетке, примыкающей к противоположной стороне и расположенной на той же горизонтали или вертикали. Метод применим также и для не всюду определенных функций. В этом случае выделяются максимальные прямоугольники, содержащие хотя бы одну единицу и не содержащие нулей.

Пример 2. Таблица 3.12 представляет собой минимизирующую карту для функции 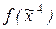с вектором значений 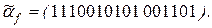Коды максимальных интервалов имеют вид (00-0), (000-), (--01), (-1-1), (110-). Сокращенная ДНФ имеет вид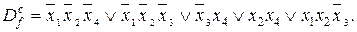

Таблица 3.12 Таблица 3.13

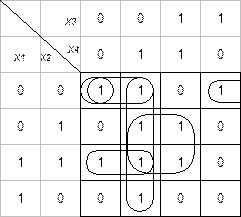
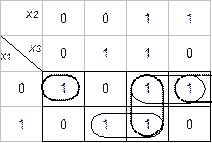
Пример 3. Таблица 3.13 представляет собой минимизирующую карту для частичной функции f, зависящей от трех переменных. Сокращенная ДНФ имеет вид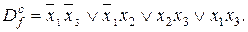

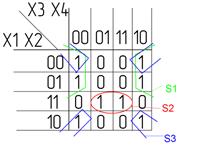Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

1) объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2ⁿ (n целое число = 0… ) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находится клеток содержащих нули;

2) область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);

3) не смежные области расположенные симметрично оси(ей) могут объединятся в одну;

4) область должна быть как можно больше, а количество областей как можно меньше;

5) области могут пересекаться;

6) возможно несколько вариантов накрытия.

Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем тоже самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.

Код Грея

Код Грея – система кодирования, в которой два соседних значения различаются только в одном разряде. Наиболее часто на практике применяется рефлексный двоичный код Грея, хотя в общем случае существует бесконечное множество кодов Грея для систем счисления с любым основанием. В большинстве случаев, под термином "код Грея" понимают именно рефлексивный бинарный код Грея.

Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.

Код получил имя исследователя лабораторий Bell Labs Фрэнка Грея. Франк Грэй (Frank Gray) был физиком и исследователем в Bell Labs (бывшая американская корпорация, крупный исследовательский центр в области телекоммуникаций, электронных и компьютерных систем), который ввёл многочисленные инновации в телевидении при помощи кода Грея.

Кодом Грея порядка n называется любая циклическая последовательность всех наборов из нулей и единиц длины n, в которой два соседних набора отличаются ровно в одной компоненте.

Пример получения кода Грея:

Начнём с первых двух чисел, закодируем их нулём и единицей:

Ноль
Один

Заметим, что они отличаются только одним битом. Проблема в том, что нам нужно больше чем два числа. Зеркально отразим коды чисел и получим:

Ноль
Один
Один
Ноль

Кодов стало больше, и соседи отличаются друг от друга не более чем одним битом. Но есть повторы. Чтобы не было повторов, допишем спереди к первой половине кодов 0, а ко второй 1.

Ноль
Один
Два
Три

Точно так же мы можем отразить и получим:

Ноль
Один
Два
Три
Три
Два
Один
Ноль

И тоже добавим в первую половину 0, а во вторую – 1.

Ноль
Один
Два
Три
Четыре
Пять
Шесть
Семь

И так далее. Таким способом можно получить код Грея любого порядка. [http://www.rsdn.ru/article/alg/gray.xml].

Младший разряд в последовательности чисел в коде Грея принимает значения 0 и 1, затем следующий старший разряд становится единичным и младший разряд принимает свои значения уже в обратном порядке (1, 0). Этим и объясняется название кода - "отражённый". Соответственно, два младших разряда принимают значения 00, 01, 11, 10, а затем, при единичном следующем старшем разряде, те же значения в обратном порядке (10, 11, 01, 00).

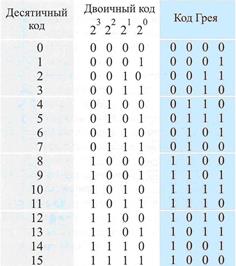
Код Грея предпочтительнее обычного двоичного тем, что обладает свойством непрерывности бинарной комбинации: изменение кодируемого числа на единицу соответствует изменению кодовой комбинации только в одном разряде. Он строится на базе двоичного по следующему правилу: старший разряд остается без изменения; каждый последующий разряд инвертируется, если предыдущий разряд исходного двоичного кода равен единице. Этот алгоритм построения может быть формально представлен как результат сложения по модулю два исходной комбинации двоичного кода с такой же комбинацией, но сдвинутой на один разряд вправо. При этом крайний правый разряд сдвинутой комбинации отбрасывается.

Таким образом, Грей-код является так называемым одношаговым кодом, т.к. при переходе от одного числа к другому всегда меняется лишь какой-то один бит. Погрешность при считывании информации с механического кодового диска при переходе от одного числа к другому приведет лишь к тому, что переход от одного положения к другом будет лишь несколько смещен по времени, однако выдача совершенно неверного значения углового положения при переходе от одного положения к другому полностью исключается. Преимуществом Грей-кода является также его способность зеркального отображения информации.

Преобразование кода Грея в двоичный код и обратно

Коды Грея легко получаются из двоичных чисел путём побитовой операции «Исключающее ИЛИ» с тем же числом, сдвинутым вправо на один бит. Следовательно, i-й бит кода Грея G_i выражается через биты двоичного кода B_i следующим образом:

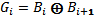
где 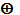– операция «исключающее ИЛИ»; биты нумеруются справа налево, начиная с младшего.

Обратный алгоритм – преобразование кода Грея в двоичный код – можно выразить рекуррентной формулой:

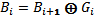
Причём преобразование осуществляется побитно, начиная со старших разрядов, и значение B_i+1, используемое в формуле, вычисляется на предыдущем шаге алгоритма. Действительно, если подставить в эту формулу вышеприведённое выражение для i-го бита кода Грея, получим

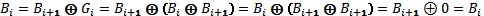
Однако приведённый алгоритм, связанный с манипуляцией отдельными битами, неудобен для программной реализации, поэтому на практике используют видоизменённый алгоритм:

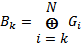
где N – число битов в коде Грея (для увеличения быстродействия алгоритма в качестве N можно взять номер старшего ненулевого бита кода Грея); знак означает суммирование при помощи операции «исключающее ИЛИ», то есть

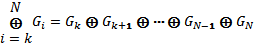
Здесь предполагается, что бит, выходящий за рамки разрядной сетки (B_N+1), равен нулю.

Ниже приведена функция на языке С, реализующая данный алгоритм. Она осуществляет последовательный сдвиг вправо и суммирование исходного двоичного числа, до тех пор, пока очередной сдвиг не обнулит слагаемое.

unsigned int graydecode(unsigned int gray)

{

unsigned int bin;

for (bin = 0; gray; gray >>= 1) {

bin ^= gray;

}

return bin;

}

Генерация кодов Грея

Рекурсивная функция построение кода Грея на языке C:

//n - требуемая длина кода,

//m - указатель на массив, способный хранить

// все коды Грея, длиной до n

// (должен быть выделен до вызова функции)

//depth - параметр рекурсии

int gray (int n, int* m, int depth)

{

int i, t = (1 << (depth - 1));

if (depth == 0)

m[0] = 0;

else {

//массив хранит десятичные записи двоичных слов

for (i = 0; i < t; i++)

m[t + i] = m[t - i - 1] + (1 << (depth - 1));

}

if (depth != n)

gray(n, m, depth + 1);

return 0;

}

Приложение Б