Участок цепи с ёмкостным элементом

Ёмкостным или С-элементом принято называть такой идеализированный элемент схемы замещения, который, в энергетическом отношении, способен лишь к преобразованию электрической энергии источника и её накоплению в виде энергии собственного электрического поля (поля зарядов). При определенных условиях он способен совершать обратное преобразование, отдавая всю накопленную энергию без остатка во внешнюю цепь (рис. 11).

iC

uC

Рис. 11.

Прообразом этого идеализированного -элемента является электротехническое устройство, называемое конденсатором и, наоборот,

С-элемент является идеализированной моделью конденсатора. Конденсаторы, кроме указанного свойства, обладают ещё рядом свойств, не являющихся для них основными, и поэтому эти свойства в модели не учитываются.

Из курса физики известно соотношение, связывающее величину заряда, накопленного конденсатором, с напряжением между его выводами

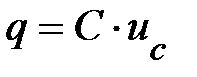_, (50)

где q – заряд на одной из обкладок конденсатора (по абсолютной величине), измеряется в кулонах (Кл); u_c – разность потенциалов между выводами конденсатора, измеряется в вольтах (В).

Параметр С – количественно характеризует способность ёмкостного элемента запасать электрическую энергию, т. е. накапливать заряды. Этот параметр называется электрической ёмкостью и измеряется в фарадах (Ф).

Известно также, что электрический ток через конденсатор имеет другую физическую природу нежели ток проводимости. Однако количественно ток через конденсатор (ток через -элемент) можно определить как скорость изменения зарядов, сосредоточенных на его обкладках

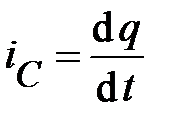. (51)

Подставив (50) в (51), получим, с учётом, что С-элемент линейный:

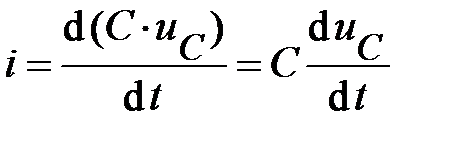. (52)

Соотношение (52), как и (40), показывают, что мгновенные значения напряжения и тока на L-элементе, а также и на С-элементе не связаны законом Ома.

Согласно определению С-элемент безвозвратно электрическую энергию не потребляет. Однако для него также как и для L-элемента можно ввести понятие о мгновенной мощности р. Под ней понимают скорость преобразования энергии, поступающей в -элемент, в энергию его собственного поля зарядов и наоборот:

.

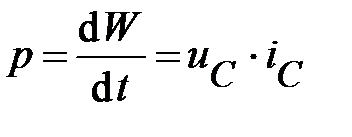отсюда получим

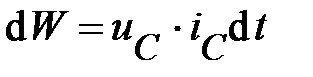
или

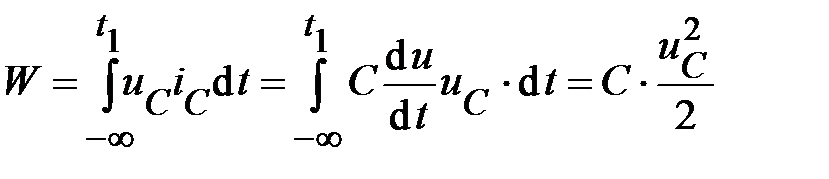. (53)

Соотношение (53) определяет энергию собственного поля С-элемента, накопленную к рассматриваемому моменту времени t₁. Заметим, что (53) также наглядно определяет параметр С, как количественную характеристику С-элемента, показывающую его способность накапливать электрическую энергию: чем больше С, тем при прочих равных условиях больше W.

Пусть к цепи с С-элементом приложено синусоидальное напряжение (рис. 11)

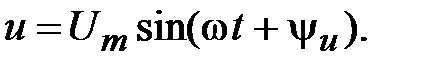
Согласно (52) определим ток, протекающий через этот элемент

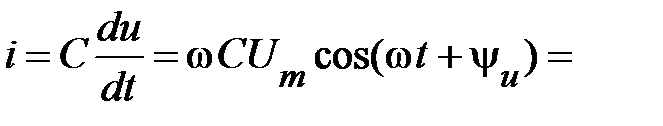
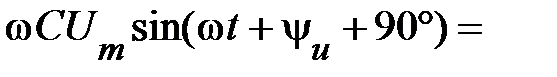
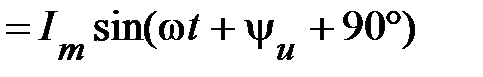. (54)

При синусоидальном напряжении ток ёмкостного элемента также синусоидален; напряжение и ток изменяются с одинаковой частотой; ток опережает напряжение по фазе на четверть периода ψ_i = ψ_u + 90 º; угол сдвига фаз φ = ψ_u – ψ_i = – 90º.

Из (49) получим закон Ома для амплитудных

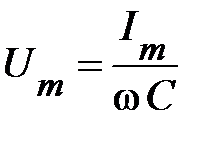(55)

или действующих значений напряжения и тока

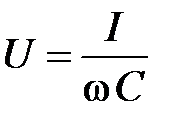. (56)

Величина 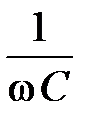имеет размерность Ом, носит название ёмкостного сопротивления -элемента и обозначается

.

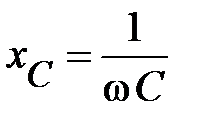В этом случае (56) можно записать так

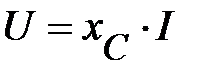(57)

Определим запись закона Ома в комплексной форме. Для этого перейдем от и 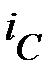как синусоидальных функций времени к однозначно изображающим их комплексам действующих значений напряжения и тока

.

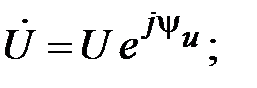
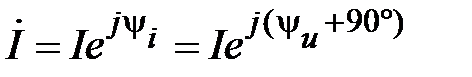Возьмем формальное отношение

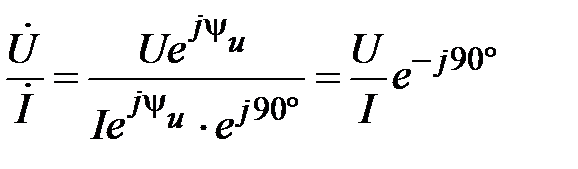. (58)

Учитывая (56) и (19), получим окончательно

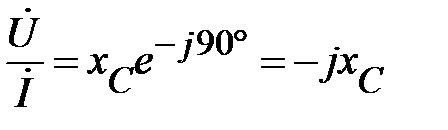или 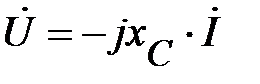. (59)

Это есть закон Ома в комплексах действующих значений напряжения и тока.

Величина jx_с называется комплексным сопротивлением ёмкостного элемента. Она условно измеряется в Омах и является отрицательным мнимым числом, модуль которого равен x_с.

Векторная диаграмма, соответствующая соотношению (59) приведена на рис. 12. На ней показано, что вектор опережает вектор на 90º.

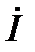+j

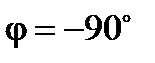ψi=ψu+90º

+1

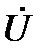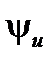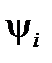Рис. 12.

Волновая диаграмма тока и напряжения на участке с С-элементом приведена на рис. 13.

ψi

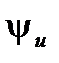π/2

u,i

ωt

ωt

i(t)

u(t)

Рис. 13

Рассмотрим энергетические процессы, протекающие в цепи с С-элементом. Мгновенная мощность на ёмкостном элементе

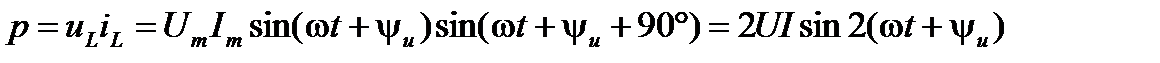. (59)

График p(t) приведён на рис.13. Видно, что мгновенная мощность в цепи с С-элементом колеблется с частотой 2ω и амплитудой U I вокруг нулевого положения. Следовательно, в этой цепи работа не совершается и энергия источника питания безвозвратно не потребляется. В тоже время происходит периодический обмен энергией между источником и элементом. Рассмотрим этот процесс.

В течение 1-ой четверти периода основной частоты (промежуток времени между точками 1 и 2 на рис.13) U > 0 и i > 0 следовательно, p > 0 т. е. С-элемент работает в режиме потребления энергии. Потребляемая энергия запасается в электростатическом поле С-элемента. В течение 2-ой четверти периода (промежуток времени между точками (2 и 3) u > 0, а i < 0, т. е. и С-элемент работает в режиме источника. Происходит обратный процесс преобразования запасённой энергии С-элементом, которая отдаётся источнику питания. Далее процесс повторяется при отрицательном напряжении.

Интенсивность обмена энергией принято характеризовать наибольшим значением скорости преобразования энергии, т. е. амплитудным значением мгновенной мощности. Как следует из (59)

.

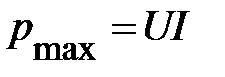С учетом (57) получим

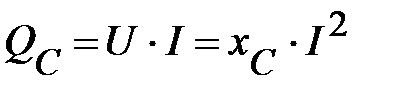(60)

Эту величину называют реактивной мощностью С-элемента. Единицей измерения этой мощности служит ВАр.

Рассмотренные модели элементарных участков цепи позволяют рассмотреть поведение более сложных участков электрических цепей. Простейшими являются модели участков с последовательным или параллельным соединением рассмотренных элементарных моделей.

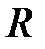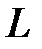6. Анализ участка схемы с последовательным соединением и - элементов

С помощью рассмотренных элементов можно изобразить линейную схему замещения любого электротехнического устройства. Например, катушку индуктивности на достаточно низкой частоте синусоидального тока можно представить следующей схемой замещения.

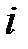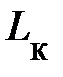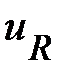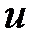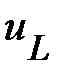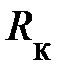Рис. 14.

Допустим известно напряжение на зажимах катушки индуктивности

.

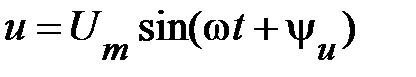(Положим ψ_u=0), а также сопротивление R_к и индуктивность L_к. Необходимо определить остальные параметры режима её работы. Согласно второго закона Кирхгофа для данной цепи можем записать уравнение для мгновенных значений напряжений:

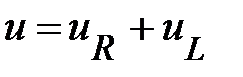(61)

или

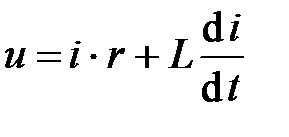. (62)

Из соотношения (62) видно, что для определения i (t) необходимо решить дифференциальное уравнение. Анализ можно упростить, если перейти к символическому методу расчета такого участка схемы. В комплексной форме уравнение (61) будет иметь вид

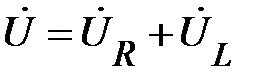. (63)

Согласно (33) и (47) это уравнение можно записать

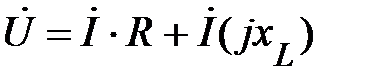. (64)

Поскольку элементы в схеме соединены последовательно, то через них протекает один и тот же ток. Тогда

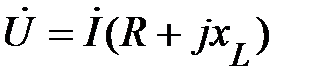. (65)

Уравнение (61) связывает общее напряжение, приложенное к этой цепи, с током, протекающим в ней. Т. е. (65) есть закон Ома для данной цепи в комплексной форме. Величина:

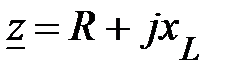(66)

измеряется (условно) в Омах и называется полным комплексным сопротивлением участка этой цепи. Эту величину можно интерпретировать в виде векторов на комплексной плоскости.

+j

+1

φ

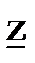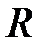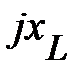Рис. 15.

Действительная часть комплексного сопротивления z

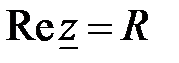
называется активным сопротивлением цепи. Мнимая её часть:

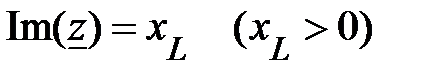
называется модулем комплексного сопротивления 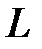-элемента. Треугольник представленный z и её составляющими на рис.15 носит название треугольника сопротивлений. Соотношение (66) определяет алгебраическую форму представления комплекса z. В расчетах получила распространение показательная форма представления z

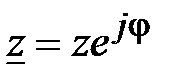, (67)

где 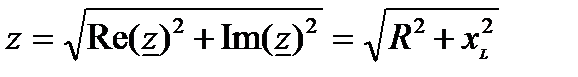носит название модуля полного комплексного сопротивления или полного сопротивления участка цепи, измеряется в Омах; 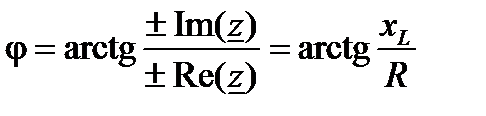носит название аргумента комплекса 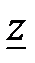или фазы полного комплексного сопротивления 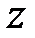, измеряется в угловых градусах или в радианах. Для сторон треугольника (рис.15) справедливы соотношения

.

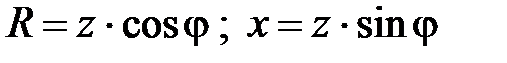С учётом (63) можно определить вектор 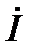из (65):

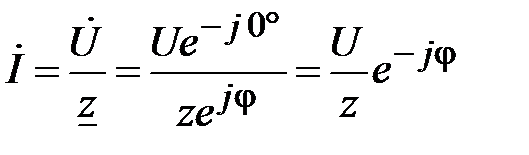(68)

x_L > 0 для линейных элементов. Тогда φ > 0 и из (68) видно, что вектор тока 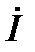в такой цепи отстаёт от вектора 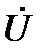на угол 0<φ<90º. Определив из (68) вектор 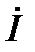, можно определить падение напряжения на каждом элементе, используя ранее установленные формулы закона Ома для этих элементов

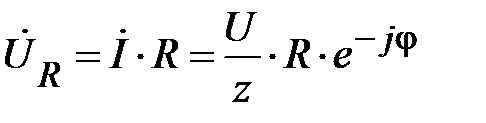; (69)

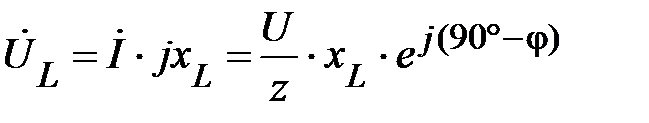. (70)

Построим векторную диаграмму (рис. 16). Построение, как было сказано ранее, начинаем с выбора масштаба по току m_i (А/см) и напряжению m_u (В/см). Определим вектор 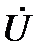заданного напряжения. Его модуль 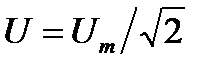, фаза ψ_u = 0, т. е. вектор располагается вдоль оси действительных чисел (+1). Откладываем от т.0 в положительном направлении оси +1отрезок длиной U/m_u (см) и его конец отмечаем стрелкой. Вектор 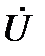построен.

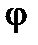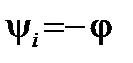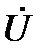N

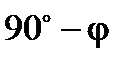+1

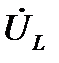+90º

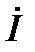M

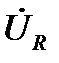K

+j

Рис. 16.

Далее строим вектор тока 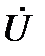. Этот вектор, как было установлено, отстаёт от вектора 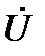на угол φ. Причём 0<φ<90º. Поэтому в IV четверти координатной плоскости проводим луч 0М под углом φ к оси +1. На этом луче от точки 0 откладываем отрезок (см). Его конец отмечаем стрелкой. Вектор 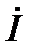построен. Строим вектор 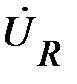. Как было установлено ранее, ток через R-элемент и падение напряжения на нём совпадают по фазе. Это подтверждают соотношения (68) и (69). Для векторной диаграммы это означает, что вектора совпадают по направлению. Поэтому на том же луче 0М от точки 0 откладываем отрезок, равный 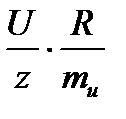(см), его конец отмечаем стрелкой. Вектор 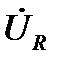построен. Наконец, строим вектор 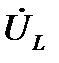. Ранее было установлено, что падение напряжения на L-элементе опережает ток через этот элемент по фазе на 90º. Это подтверждают соотношения (68) и (70). Для векторной диаграммы данный ввод означает, что вектор 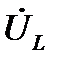должен быть перпендикулярен вектору 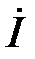и направлен в сторону оси +1 (поскольку разность фаз между 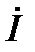и 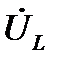составляет +90º, а за положительное направление при повороте векторов в электротехнике принято направление против часовой стрелки). Из конца вектора 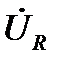(точка К на рис. 16) восстанавливаем перпендикуляр к лучу 0М в направлении оси +1. На перпендикуляре КN от точки К откладываем отрезок длиной, равной 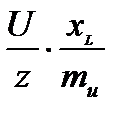(см). Конец этого отрезка отмечаем стрелкой. Вектор 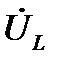построен. В случае верного построения всех векторов на данной диаграмме, конец вектора 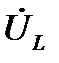совпадает с концом вектора 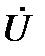. Т. е. сумма векторов 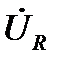и 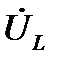равна вектору 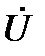, что является геометрической интерпретацией 2-го закона Кирхгофа для данной цепи (63).

Рассмотренные вектора 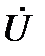, , 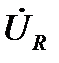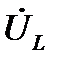образуют прямоугольный треугольник, называемый треугольником напряжений. Для сторон этого треугольника справедливы соотношения:

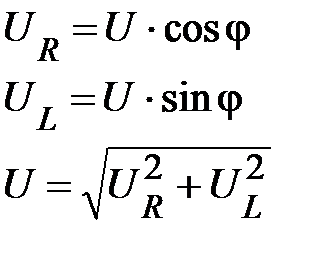. (71)

В заключение проанализируем энергетические процессы, протекающие в этой цепи. Как было установлено, интенсивность энергетических процессов, протекающих на участке цепи с R-элементом, можно характеризовать активной мощностью:

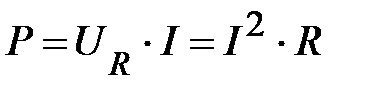, (72)

а интенсивность процессов, протекающих на участке цепи с L-элементом – реактивной мощностью:

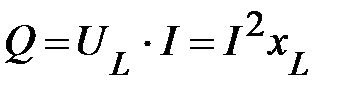. (73)

Поскольку в данной цепи включён R-элемент, то часть энергии источника питания будет безвозвратно потребляться на R-элементе. В то же время из-за наличия L-элемента в этой цепи будет происходить непрерывный обмен (с частотой 2ω) энергией (циркуляция энергии) между магнитным полем L-элемента и источником питания. Для характеристики общего энергетического режима цепи вводят понятие о полной мощности.

Определим её величину. Из (71) и (72) можно записать

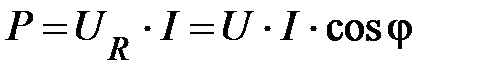(74)

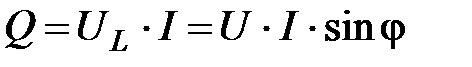(75)

Возведём в квадрат (70) и (71) и сложим полученные результаты

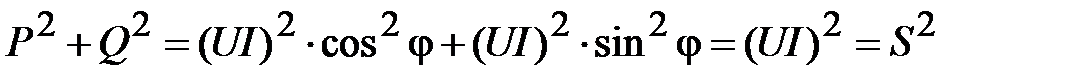(76)

или

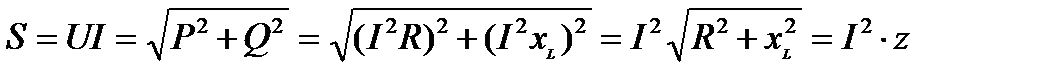,(77)

где S – полная мощность этого участка цепи, измеряемая в вольтамперах (ВА).

Можно записать соотношение между полной мощностью и её составляющими в комплексной форме. Для этого каждую сторону треугольника сопротивлений (рис. 15) умножим на 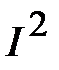. Вновь образованный прямоугольный треугольник (рис. 17) определяет своей гипотенузой полную мощность, а катетами – активную и реактивную мощности. Данный треугольник называется треугольником мощностей. Его стороны связаны соотношением:

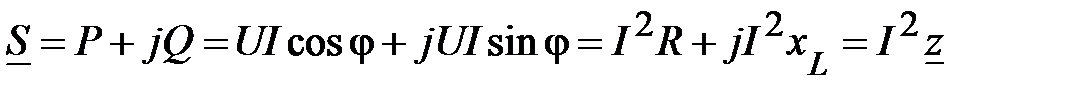. (78)

S – полная комплексная мощность данного участка цепи. Её модуль

.

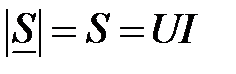+j

+1

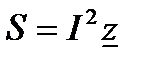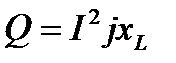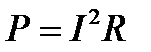Рис. 17.

Полная мощность и её составляющие измеряются единицами мощности одинакового масштаба. Однако для того, чтобы подчеркнуть разную физическую природу энергетических процессов, интенсивность которых они оценивают, эти единицы измерения называют по-разному:

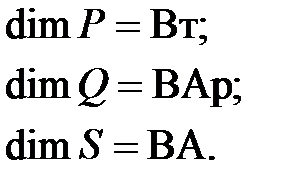
Треугольники сопротивлений (рис. 15), напряжений (рис. 16) и мощностей (рис.17) подобны. Из этого, в частности, следует, что

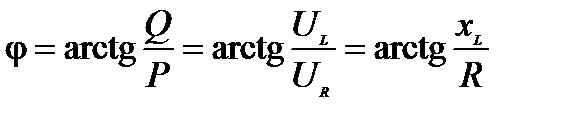.(79)

Предоставляем студентам самостоятельно провести аналогичный анализ для участка цепи, содержащего последовательное соединение R и C-элементов.