Основные сведения о цепях синусоидального тока

Перед выполнением лабораторных работ, посвящённых исследованию цепей синусоидального тока, весьма полезным является изучение соответствующих разделов по лекциям или учебникам. Данный раздел не претендует на выполнение этой цели и служит для первоначального знакомства с основными понятиями и элементами цепей синусоидального тока.

Формы представления синусоидальных напряжений,

ЭДС и токов

Допустим, что имеем некоторую цепь, в которую включены источники питания (источники ЭДС или источники тока), вырабатывающие синусоидальную ЭДС или синусоидальный ток одной частоты, а также приёмники (резисторы, катушки индуктивности, конденсаторы). Для того, чтобы экспериментально или теоретически изучить режим работы такой цепи (а может быть и область возможных режимов работы), необходимо, прежде всего, уяснить, каким образом представлять синусоидально изменяющиеся во времени параметры режимов работы этой цепи. Т.е., иными словами, в какой форме представлять синусоидальные напряжения, ЭДС или ток для того, чтобы с этими представлениями можно было удобно и наглядно проводить расчёты или измерения.

Известно, что любую функцию можно представить в аналитической, графической и табличной формах.

Широко распространенные ранее таблицы значений sin x (x изменяется от 0 до 90 угловых градусов) в настоящее время вытеснены в результате массового производства микрокалькуляторов. Поэтому табличное представление указанных величин в практике расчётов по электротехнике в настоящее время не используется.

Как следует из определения, аналитическая форма представления указанных параметров режимов может быть записана в виде:

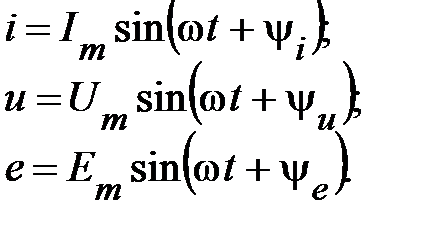(1)

Для уяснения смысла всех параметров, указанных в (1), приведём графическую форму представления синусоидальных величин (рис.1) и составим эти формы.

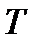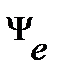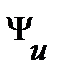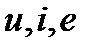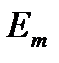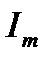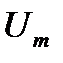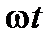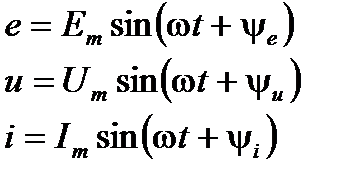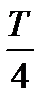Рис. 1.

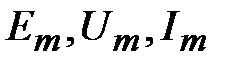– амплитудное значение ЭДС, напряжения и тока, т. е. максимальное по абсолютной величине значение параметра режима, которое он может принимать в течение времени. Амплитудные значения измеряются в Вольтах (В) или Амперах (А), соответственно. По оси абсцисс на графике (рис.1) в качестве аргумента принято брать параметр 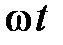, имеющий размерность – радианы, и пропорциональный времени .

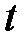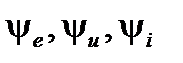– начальная фаза ЭДС, напряжения и тока, которая показывает, какую величину составляет рассматриваемый параметр режима ( 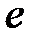, 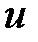или 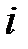) в момент времени, принятый за начало отсчёта 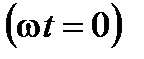. Иными словами начальная фаза определяет сдвиг графика синусоиды вдоль оси времени 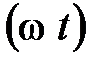относительно начала отсчёта. Если в момент 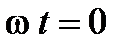(начала отсчёта) рассматриваемая синусоидальная величина отрицательна, то её начальная фаза

,

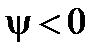в противном случае

.

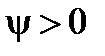Поэтому количественно начальная фаза 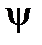определяется вдоль оси абсцисс от ближайшего к началу координат нулевого значения синусоидальной величины при её переходе от отрицательных значений к положительным относительно оси абсцисс. Если начальная фаза положительна, то начало синусоидальной величины сдвинуто влево, в противном случае – вправо от начала координат. Так на рис.1 начальная фаза тока 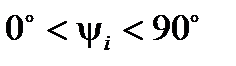– положительна; начальная фаза ЭДС 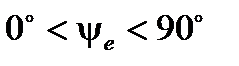– положительна; кроме этого 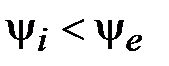. наконец, начальная фаза U 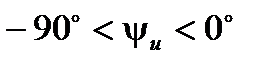- отрицательна. Начальная фаза измеряется в угловых градусах или радианах.

Аргумент синусоидальной величины 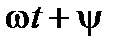носит название фазы (фазы колебаний). Она измеряется в радианах или угловых градусах и показывает, в какой фазе находятся колебания напряжения, ЭДС или тока в данный момент времени. Как видно (рис.1), при различных значениях фазы колебания можно получить одинаковые значения функции.

Для того чтобы анализировать многозначные синусоидально изменяющиеся функции, их принято рассматривать на участке вдоль оси абсцисс с полным циклом изменения фазы колебаний. Такой участок называется периодом колебаний и определяется как минимальный промежуток времени (или минимальное расстояние вдоль оси абсцисс) между двумя одинаковыми значениями синусоидальной функции. Период 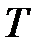измеряют в секундах; для аргумента 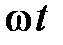период равен 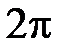радиан или 360º.

Величину обратную периоду колебаний 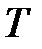называют циклической частотой колебаний

_.

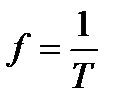Циклическая частота 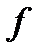измеряется в Герцах и показывает какое число полных циклов колебаний (или периодов) данной синусоидальной функции происходит в одну секунду.

Также важным параметром является угловая частота колебаний

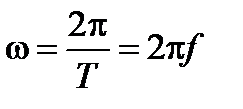(радиан/секунда или угловые град / секунда).

Весьма важным понятием в электротехнике является разность фаз 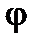, под которой понимают сдвиг графиков синусоидальных величин один относительно другого. Разность или сдвиг фаз, например, между синусоидальными напряжением и током одинаковой частоты (рис.1) можно определить как разность их начальных фаз

.

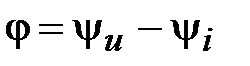Аналогично разность фаз между 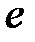и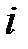

.

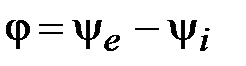Следует помнить, что поскольку начальная фаза есть величина алгебраическая, то разность фаз также величина алгебраическая. И ещё одно важное обстоятельство. Начальная фаза колебаний зависит от момента времени, принятого за начало отсчёта 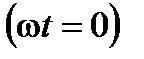, в то же время разность фаз не зависит или, говорят, инвариантна относительно начала координат, если частота синусоидальных функций, между которыми определяется 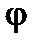, одинакова.

Как видно, аналитическая и графическая формы представления синусоидальных величин определяется сравнительно большим числом параметров, поэтому они не нашли применения в расчетах и используются, преимущественно, для наглядного представления результатов расчёта или измерения.

Необходимость оценки или измерения синусоидальных ЭДС, напряжений и токов с помощью одного какого-либо параметра привела к появлению различных эквивалентов. Наибольшее распространение получило действующее значение синусоидального тока, которое является его тепловым эквивалентом и определяется такой величиной постоянного тока, который производит такой же тепловой эффект, что и оцениваемый синусоидальный ток, протекая через тот же 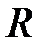-элемент (с тем же сопротивлением), что и синусоидальный ток за одно и то же время. Если в линейной цепи действуют синусоидальные ЭДС, то действующее значение синусоидального тока определяется как

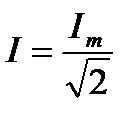, (2)

где 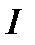– действующее значение синусоидального тока; 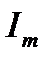– амплитудное значение синусоидального тока. По аналогии определяются действующие значения синусоидального напряжения и ЭДС:

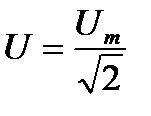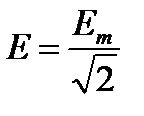; . (3)

Следует заметить, что этот эквивалент для синусоидальных напряжений и ЭДС не имеет конкретного физического смысла, как для тока, так и для напряжения.

Действующее значение синусоидального тока, напряжения или ЭДС нашло широкое применение в измерительной технике. Многие измерительные приборы (вольтметры, амперметры), используемые в электротехнических измерениях, проградуированы в действующих значениях напряжения и тока.

Несмотря на это данный эквивалент не может однозначно описать указанные синусоидальные величины, поскольку ничего не говорит о фазе колебаний. Как будет показано в дальнейшем, одинаковые действующие значения синусоидального тока и напряжения при различной величине сдвига фаз между ними обеспечиваются различными энергетическими явлениями в цепи. Поэтому только использование действующего значения оказывается явно недостаточным при расчетах.

Попытки преодолеть указанные недостатки привели к представлению синусоидальных функций времени их изображением в виде вращающихся радиус-векторов в декартовой плоскости координат. На рис.2 представлен радиус-вектор 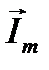, длина которого равна 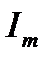. Данный вектор вращается в декартовой плоскости координат 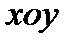против часовой стрелки с постоянной угловой скоростью 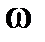и поворачивается за время одного оборота 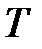на угол 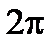, т.е. 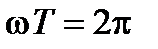. Положение радиус-вектора 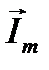относительно оси 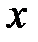в момент начала отсчёта времени 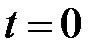определяется углом 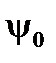. За отрезок времени 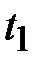радиус-вектор повернётся на угол 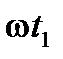и его положение относительно оси 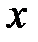определится углом 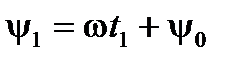. За время 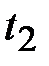радиус-вектор переместится на угол 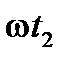и займёт положение, определяемое углом 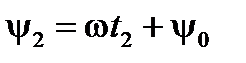и т.д. Проекция вращающегося радиус-вектора на ось 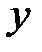в момент времени 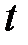определится выражением 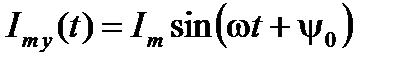. Очевидно, при 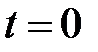величина вектора составит 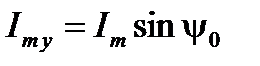(отрезок 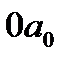) и т.д. На этом же рис. 2 построена синусоида, мгновенные значения которой для любого момента времени 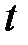найдены как соответствующие проекции вращающегося радиус-вектора на ось 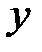в тот же момент времени.

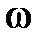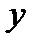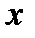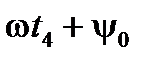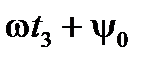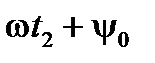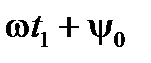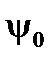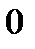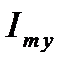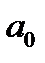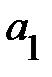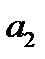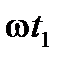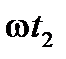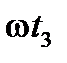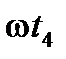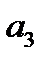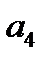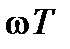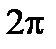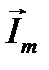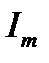Рис. 2.

На основании приведённых построений можно утверждать, что между вращающимся радиус-вектором и некоторой синусоидальной функцией времени существует взаимно однозначное соответствие. А именно, любому равномерно вращающемуся радиус-вектору однозначно соответствует некоторая синусоидальная функция времени. И, наоборот, любая синусоидальная функция времени может быть условно изображена однозначно соответствующим ей вращающимся радиус-вектором, длина которого равна амплитудному значению синусоиды, а начальное положение относительно оси 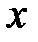определяется начальной фазой синусоиды.

Такое представление синусоидальных функций времени может быть использовано в расчётах цепей переменного тока.

Допустим, для некоторого узла электрической цепи по первому закону Кирхгофа можно записать уравнение:

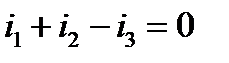
или

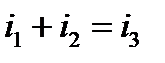. (4)

При этом для 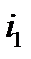и 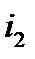известны аналитические выражения

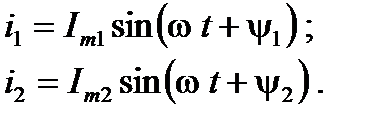(5)

Путём элементарных тригонометрических преобразований можно показать, что сумма двух синусоид одинаковой частоты 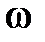представляет собой синусоиду той же частоты . Т.е. данный расчёт сводится к определению 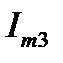и 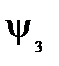в выражении

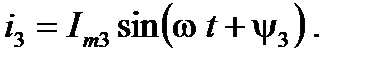(6)

Если воспользоваться аналитическим представлением синусоидальных токов 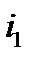, 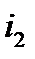и 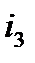, то искомые параметры можно получить с помощью известных тригонометрических преобразований:

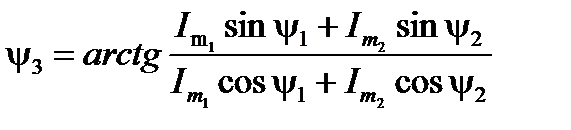
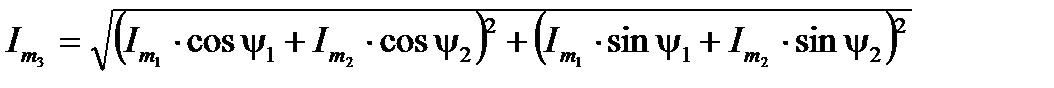(7)

Как видно, решение задачи получается громоздким даже в том случае, когда суммируются только две функции, в то время как задачи электротехники очень часто требуют суммирования нескольких величин.

Ещё боле громоздким и к тому же менее точным получается решение этой задачи, если её проводить для графического представления синусоидальных величин (рис.1). В этом случае необходимо предварительное построение графиков заданных токов 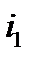и 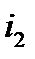, как функции времени. Затем с их помощью, путём суммирования ординат графиков 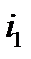и 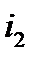для фиксированных моментов времени, построения графика тока 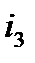. И, наконец, с помощью построенного графика, определение 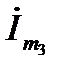и .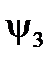

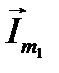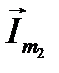Проведём решение задачи с помощью радиус-векторов и вращающихся с частотой 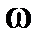против часовой стрелки. На рис.3 показаны их положения для момента времени 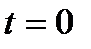. Результирующий вектор 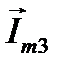, полученный сложением 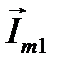и 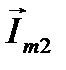по правилу параллелограмма, будет также вращаться с частотой и являться в свою очередь изображением некоторой синусоидальной функции времени.

Рис. 3.

Учитывая, что

;

,

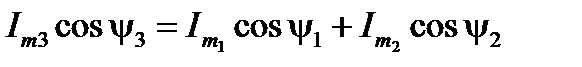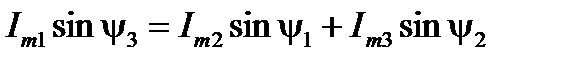получим, что для модуля 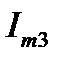и начальной фазы 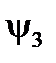результирующего вектора 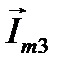справедливы соотношения (7). Следовательно, 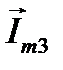является изображением искомого тока 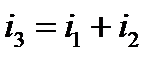. Зная выбранный масштаб, можно определить амплитуду тока 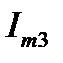. Непосредственно по чертежу (рис.3) определяется и начальная фаза 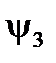. Следует обратить внимание на то, что если все вектора вращаются с одинаковой частотой, то со временем их положения друг относительно друга не изменяется. Поэтому, в принципе, безразлично в какой момент времени рассматривать указанную диаграмму векторов.

В электротехнике принято такие диаграммы строить для момента времени 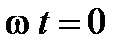, т.е. принято считать, что графическим изображением синусоидальной электрической величины может служить и неподвижный радиус-вектор. Длина этого вектора равна (в выбранном масштабе) амплитудному значению синусоидальной величины, а угол относительно положительного направления оси абсцисс равен её начальной фазе. При этом направление движения векторов против часовой стрелки считается положительным, а по часовой – отрицательным. Аналогично определяется знак угла 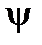радиус-вектора. Так на рис.3 все углы 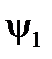, , 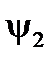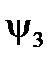положительны.

Такую совокупность радиус-векторов, отображающих синусоидальные величины одной и той же частоты при 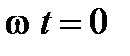, и учитывающую правильную ориентацию этих векторов по фазе, принято называть векторной диаграммой.

Расчёты с использованием изображающих векторов просты и наглядны, однако обладают существенным недостатком, присущим всем графическим методам, – ограниченной точностью.

В конце XIX века Ч. П. Штейнмецем и А.Е. Кеннели был предложен символический метод расчёта, основанный на представлении синусоидальных напряжений, токов и ЭДС в виде векторов на комплексной плоскости. Комплексные изображения позволяют совместить простоту и наглядность векторных диаграмм с возможностью проведения точных аналитических расчётов.

Некоторый вектор, изображающий синусоидальную функцию времени в декартовой плоскости, перенесём на комплексную плоскость, для чего совместим ось x с осью действительных чисел, а ось y с осью мнимых чисел (рис.4). Если при замене координат мы сохраним все условия изображений, о которых было сказано выше, то такой перенос даёт возможность аналитического выражения радиус-вектора.

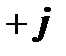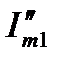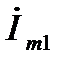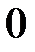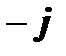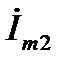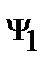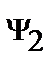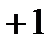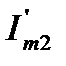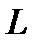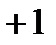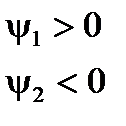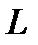Рис. 4.

Комплексный вектор принято обозначать в виде 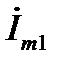или 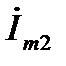, имея в виду, что 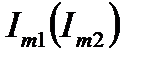– его модуль, а 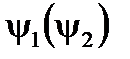– его аргумент или фазовый угол. Известно, что любому вектору 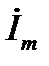, расположенному на комплексной площади, однозначно соответствует комплексное число, которое может быть записано в трёх формах:

алгебраической

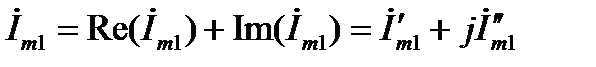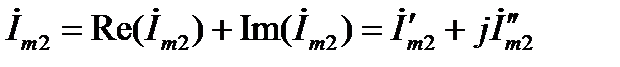; ;(8)

тригонометрической

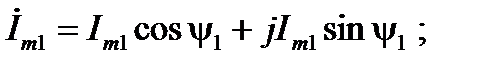
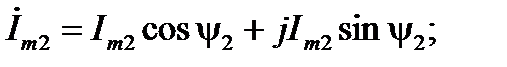(9)

показательной

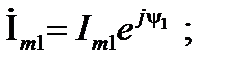
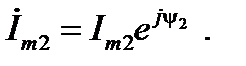(10)

Здесь символом 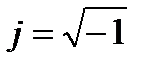обозначена мнимая единица, 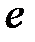– основание натурального логарифма, 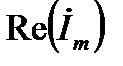– действительная часть комплексного числа, 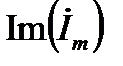– его мнимая часть. В соответствии с формулой Эйлера, все три формы равнозначны: